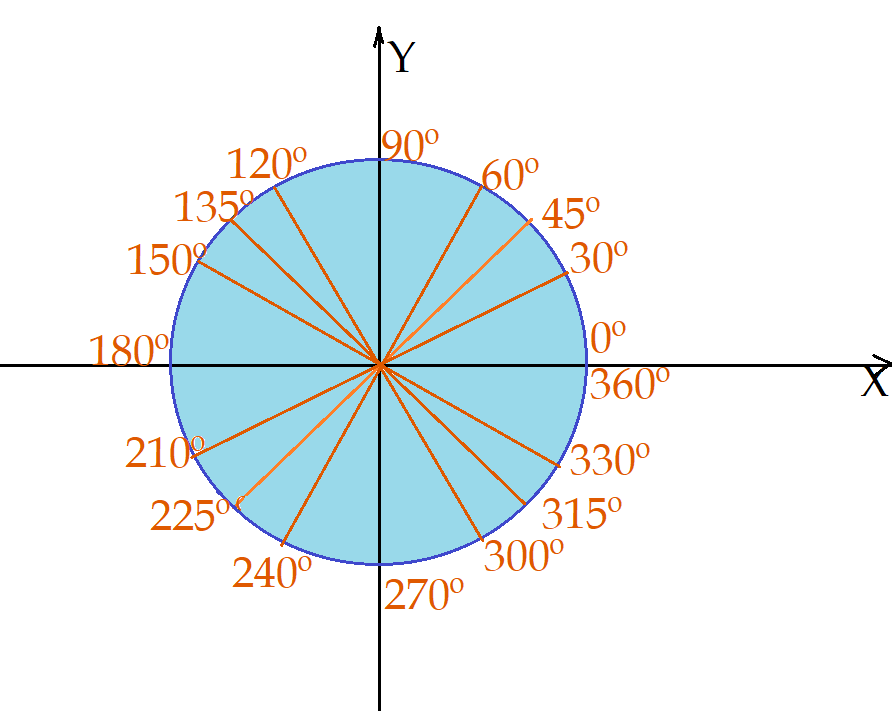
As razões trigonométricas podem ser estudadas com mais detalhes no que é denominado círculo trigonométrico. Traçamos um círculo, cujo raio convencionamos sendo igual a unidade ($r = 1$). O centro desse círculo se localiza nas coordenadas $(0,0)$ de um plano cartesiano $XOY$. O ponto de intercessão desse círculo com o semi-eixo positivo de , $\overrightarrow{OX}$, é convencionado como sendo a origem dos arcos crescentes. O sentido positivo desses arcos é o anti-horário. Essa convenção é adotada no mundo inteiro.
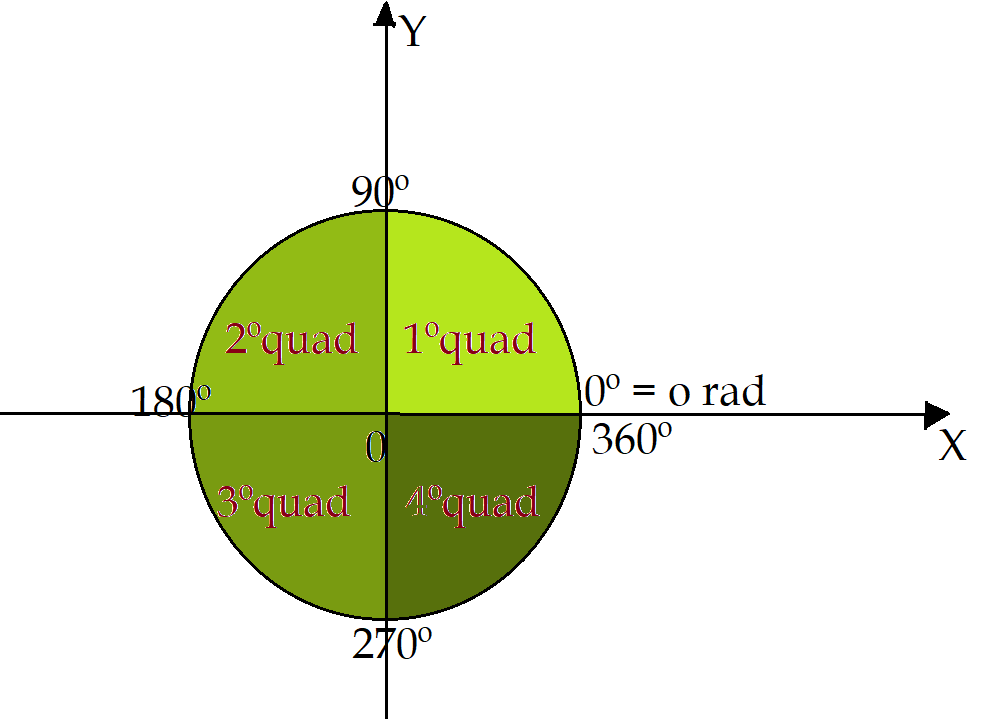
Os eixos cartesianos $XOY$, dividem o círculo trigonométrico em quatro partes iguais, denominadas quadrantes. Obedecendo ao sentido dos arcos crescentes, anti-horário, temos:
$0^{0}\leq\alpha\leq(90^{0})$$\rightarrow$ primeiro quadrante;
$(90^{0})\leq\alpha\leq(180^{0})$$\rightarrow$ segundo quadrante;
$(180^{0})\leq\alpha\leq(270^{0})$$\rightarrow$ terceiro quadrante;
$(270^{0})\leq\alpha\leq(360^{0})$$\rightarrow$ quarto quadrante.
Isto completa uma volta ou seja o retorno à posição da origem dos arcos crescentes $(360^{0})\leqq(0^{0})$.
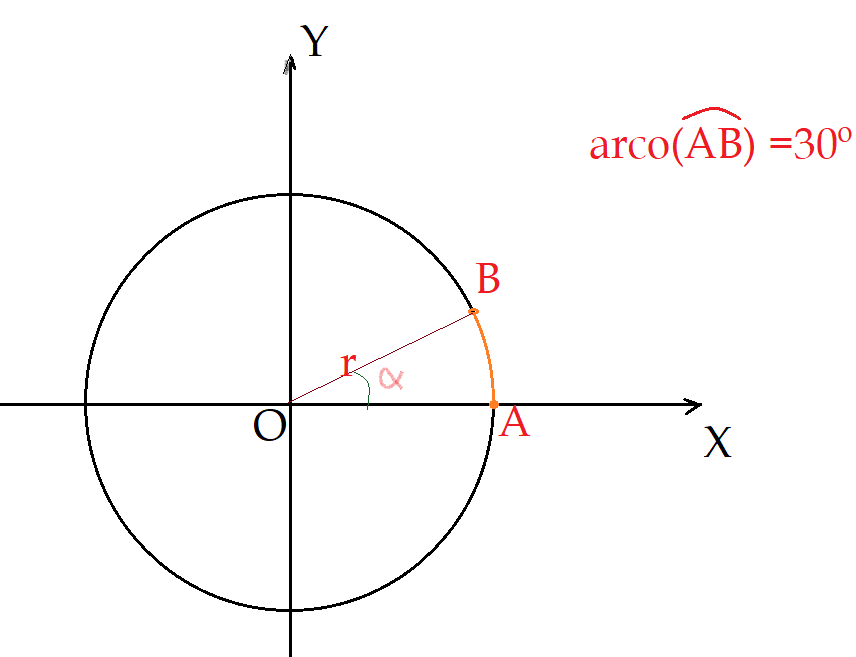
Imagine um ponto colorido existente na periferia de uma roda, que gira em torno de um eixo. Se ela girar no sentido dos arcos crescentes (anti-horário), esse ponto irá ocupar uma posição diferente a cada instante. O arco descrito tem a medida denominada pela letra $l$, e o raio do arco tem medida $r$, no círculo trigonométrico. A divisão do comprimento desse arco, pelo raio do círculo, nos dará a medida do ângulo em radianos.
$\alpha = \frac{l}{r}\, rad$
A unidade radiano, como se pode perceber, é definida em função dos elementos do arco. Podemos considerar essa unidade como a unidade natural de ângulos ou arcos. O arco tem o mesmo valor numérico do ângulo, por conta do fato de o raio do círculo trigonométrico ser unitário.
Já a unidade que é mais usada em alguns casos para medir os ângulos é o grau e sua subdivisão em minutos. Estes por sua vez são divididos em segundos. Assim, se um ângulo medir a graus, b minutos e c segundos, escreveremos essa medida da seguinte forma:
$$\alpha = a^{0}b’c”$$.
Em um círculo completo temos $360^{0}$. (Herança do sistema sexagesimal de numeração deixada pelos povos Fenícios e seus ancestrais).
Do estudo da circunferência, sabemos que ela, retificada, isto é, aberta e esticada, mede ${C = 2\pi\cdot r}$
O que nos permite estabelecer que uma volta completa do ponto sobre o círculo, terá descrito um arco de:
$(360^{0}) = 2\pi \,rad$
Expressão Geral dos arcos côngruos
É possível obter inúmeras determinações de um mesmo ângulo, todas elas diferindo entre si de um número inteiro de voltas completas sobre o círculo trigonométrico. Estes arcos são denominados arcos côngruos. Apenas para dar um exemplo, vejamos:
$\frac{1}{3}\cdot \pi \, rad= 2\pi + \frac{1}{3}\cdot\pi\, rad = 4\pi + \frac{1}{3}\cdot\pi\, rad = 6\pi + \frac{1}{3}\cdot\pi \, rad = 8\pi + \frac{1}{3}\cdot\pi \, rad =…..$
Os coeficientes são números pares, pois uma volta completa é igual a $360^{0} = 2\pi\, rad$.
Usando para simbolizar o número inteiro de voltas a letra grega $\kappa$, podemos escrever a expressão dos arcos côngruos, para qualquer arco, dessa forma:
$\alpha = 2\kappa\pi +\frac{n}{D}\cdot\pi \, rad$
O último termo da expressão geral $\frac{n}{D}\cdot\pi $ é a menor determinação positiva do arco. Podemos entender como sendo a parte do arco menor do que uma volta completa sobre o círculo. A razão $\frac{n}{D} \lt 2$ o que implica em $n\lt{2D}$.
O primeiro termo representa o arco total descrito por um ponto em ciclos, ao redor do eixo de rotação que passa pelas coordenadas $(0,0)$ e é perpendicular ao plano $XOY$, nesse ponto.
No caso de o arco ser medido em graus, iremos dividir sua medida por $360^{0}$. O quociente inteiro será o número de voltas $\kappa$ e o resto será $\alpha $, a menor determinação positiva. Resumindo as duas formas de escrever a expressão geral dos arcos côngruos, temos:
$\gamma = 2\kappa\pi + \frac{n}{D}\pi$
$\gamma = \kappa\cdot{360^{0}} + \alpha$
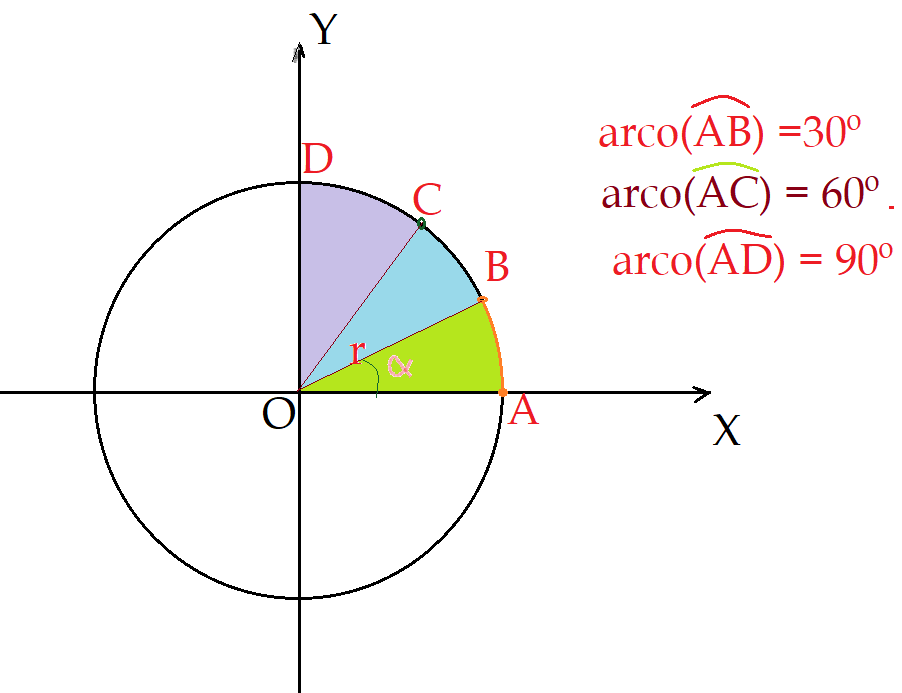
No círculo trigonométrico, fica bem mais simples visualizar e entender as razões trigonométricas. Para cada ângulo, temos um arco correspondente. O vértice sempre está sobre o centro do círculo. As coordenadas do ponto que representa a extremidade do arco, no plano cartesiano, representam os catetos de um triângulo retângulo. O raio unitário é a hipotenusa. Observemos a figura.
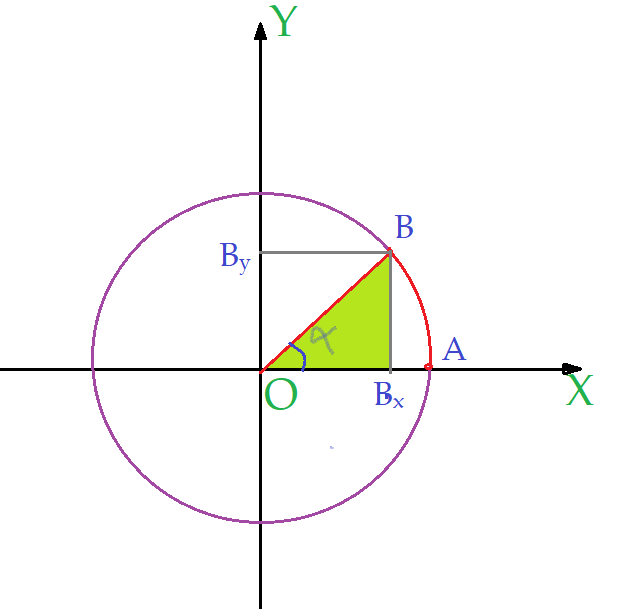
O arco $\widehat{AB}$, subtende o ângulo central $\alpha$. Os segmentos $\overline{BB_x}$ e $\overline{B_yO}$ têm a mesma medida e esta é o cateto oposto ao ângulo central subtendido pelo arco. Os segmentos $\overline{BB_y}$ e $\overline{B_xO}$, têm a mesma medida e representam o cateto adjacente ao ângulo central. O segmento $\overline{OB}$ é o próprio raio unitário do círculo trigonométrico e, como vimos, é a hipotenusa do ângulo central subtendido pelo arco.
Assim: $sen\alpha = {\frac{\overline{BB_x}}{\overline{OB}}} = \frac{y}{r}$
$cos\alpha ={\frac{\overline{B_xO}}{\overline{OB}}}=\frac{x}{r}$
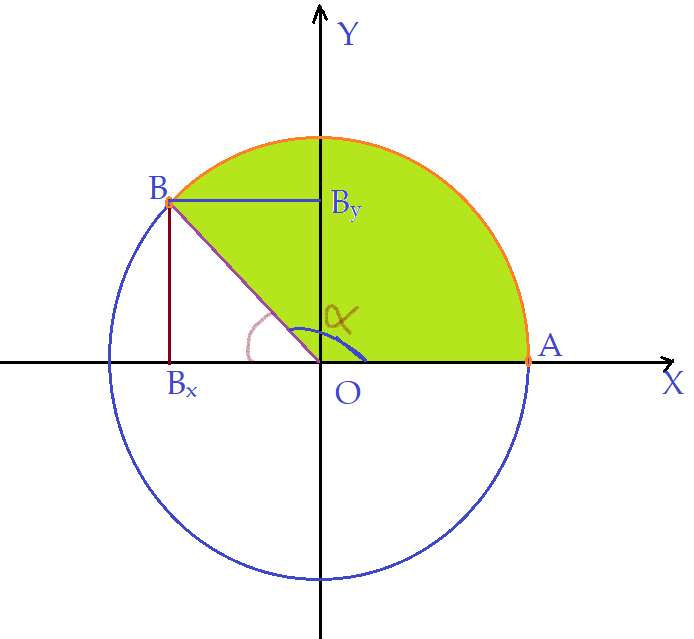
Nessa nova figura, o arco $\widehat{AB}$ tem a extremidade $B$ no segundo quadrante e portanto o ângulo central subtendido pelo arco está compreendido no intervalo ${\frac{\pi}{2}\leq\alpha\leq{\pi}}$. Podemos notar que a projeção da extremidade sobre o eixo $X$, é um valor negativo, ou seja, o cateto adjacente para cálculo das razões trigonométricas é ${\overline{B_xO}\lt0}$.
Temos: $sen\alpha = {\frac{\overline{BB_x}}{\overline{OB}}}=\frac{y}{r}$
$cos\alpha=\frac{\overline{B_xO}}{\overline{OB}}= – \frac{x}{r}$
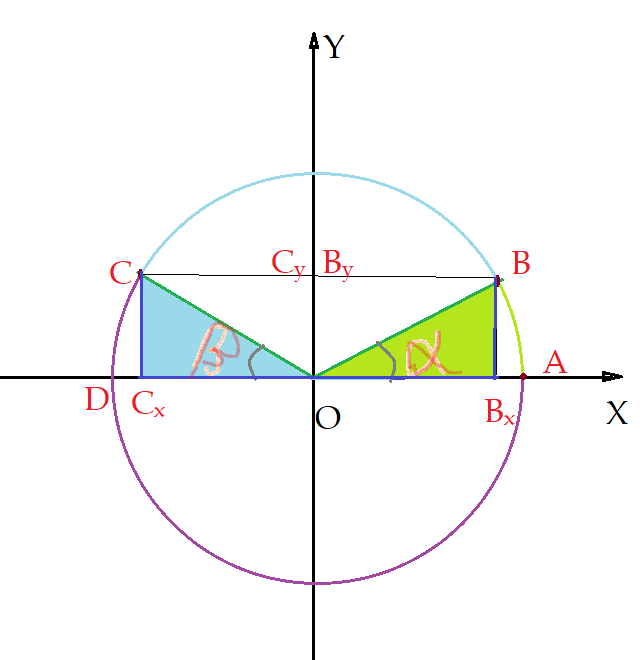
Podemos notar que para cada arco do primeiro quadrante, existe um outro, cuja extremidade fica no segundo quadrante. São os denominados ângulos suplementares. Eles têm a característica de possuírem o mesmo valor para o seno e valores simétricos para o cosseno. Isso pode ser observado nas figuras ao lado e a seguir. Vejamos a primeira figura. Percebe-se facilmente que os arcos $\widehat{AB}$ e $\widehat{AC}$, subtendem dois ângulos que, somados totalizam $(180^{0}) = {\pi} rad$. As projeções dos pontos $B$ e $C$ sobre os eixos cartesianos, são $\overline{BB_x} = \overline{CC_x}$ e $\overline{CC_y}=-\overline{BB_y}$, de modo que os valores do seno para ambos são iguais, enquanto os valores do cosseno são simétricos. Isso é sempre válido, em qualquer situação, para ângulos suplementares.
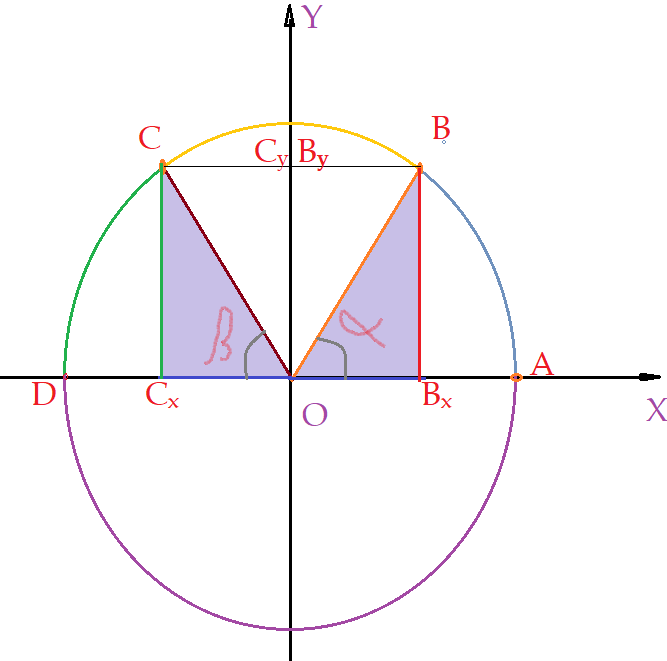
Se fizermos essa observação para todos os pares de ângulos suplementares que possamos imaginar, verificaremos que sempre ocorrerá a mesma coisa. Portanto a razão $sen\alpha$ para todos os ângulos compreendidos entre $(0^{0})\lt\alpha\lt(180^{0})$ é positiva. Já a razão $cos\alpha$ é positiva no intervalo entre $0^{0}\leq\alpha\lt(90^{0})$ e negativa para o intervalo entre $(90^{0})\lt\alpha\leq(180^{0})$.
Vejamos como se comportam as razões trigonométricas do terceiro quadrante, isto é, para ângulos no intervalo entre $(180^{0}\leq\alpha\leq(270^{0})$.
Um arco de origem $(0^{0})$ e extremidade no terceiro quadrante do círculo trigonométrico, tem projeções ortogonais $\overline{B_{x}O}$ e $\overline{B_{y}O}$, ambas negativas e por tal motivo, tanto a razão “seno” quanto a razão “cosseno” é negativa.
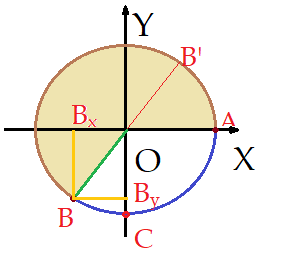
Prolongando o segmento $\overline{BO}$ para o primeiro quadrante, determinamos o ângulo equivalente no primeiro quadrante. Esse procedimento denominamos redução ao primeiro quadrante. Isso nos permite memorizar mais facilmente os valores das razões trigonométricas, que são iguais em módulo. Os sinais veremos numa tabela resumo daqui a pouco.
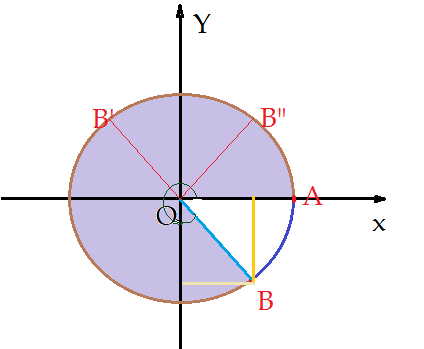
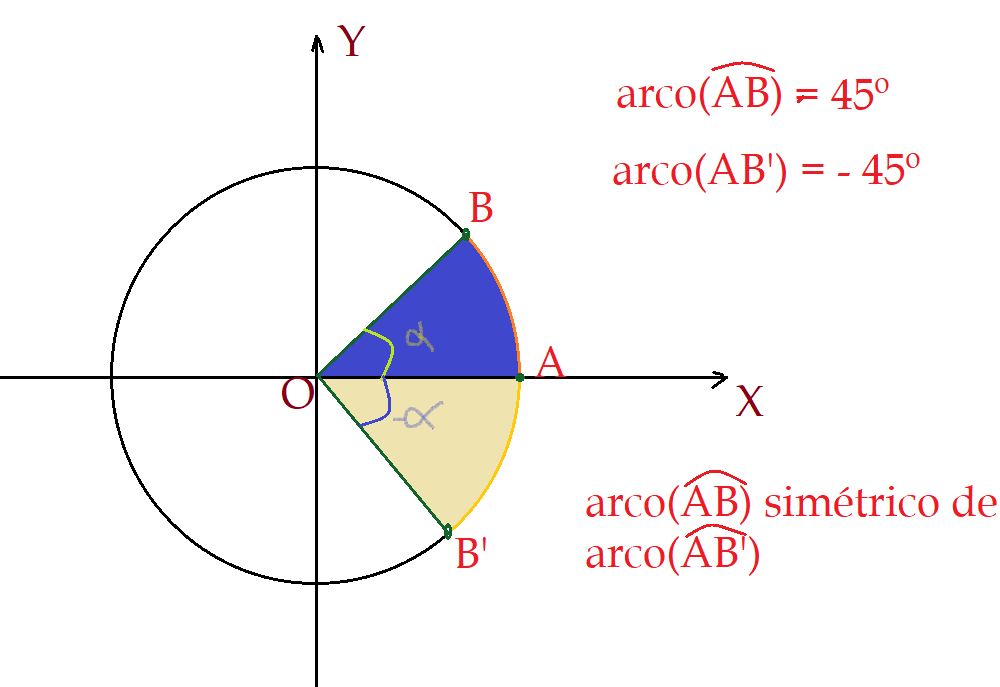
Um arco $\widehat{AB}$, com extremidade no quarto quadrante, tem as projeções ortogonais com sinal positivo no eixo $X$ e negativo no eixo $Y$. Desse modo teremos a razão seno negativa e a razão cosseno positiva. O prolongando o raio $\overline{OB}$, até encontrar o círculo no segundo quadrante, no ponto $B’$,s podemos depois encontrar o correspondente no primeiro quadrante. O arco $\widehat{AB”}$ é simétrico do arco $\widehat{BA}$, implemento de $\widehat{AB}$
A seguir vamos construir uma tabela com os valores das principais razões trigonométricas em uma volta completa do círculo trigonométrico.
| $ângulo$ | sen | cos | tg | ctg | sec | csc |
| $0^{0}$ | 0 | 1 | 0 | $\pm\infty$ | 1 | $\infty$ |
| $30^{0}=\frac{\pi}{6}$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{3}}{3}$ | ${\sqrt{3}}$ | $\frac{2\sqrt{3}}{3}$ | 2 |
| $45^{0}=\frac{\pi}{4}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | 1 | 1 | ${\sqrt{2}}$ | ${\sqrt{2}}$ |
| $60^{0}=\frac{\pi}{3}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ | ${\sqrt{3}}$ | $\frac{\sqrt{3}}{3}$ | 2 | $\frac{2\sqrt{3}}{3}$ |
| $90^{0}=\frac{\pi}{2}$ | 1 | 0 | $\pm\infty$ | 0 | indet | 1 |
| $120^{0}=\frac{2\pi}{3}$ | $\frac{\sqrt{3}}{2}$ | ${-\frac{1}{2}}$ | $-{\sqrt{3}}$ | ${-\frac{\sqrt{3}}{3}}$ | -2 | $\frac{2\sqrt{3}}{3}$ |
| $135^{0}=\frac{3\pi}{4}$ | $\frac{\sqrt{2}}{2}$ | ${-\frac{\sqrt{2}}{2}}$ | -1 | -1 | ${-\sqrt{2}}$ | ${\sqrt{2}}$ |
| $150^{0}=\frac{5\pi}{6}$ | $\frac{1}{2}$ | ${-\frac{\sqrt{3}}{3}}$ | ${-\frac{\sqrt{3}}{3}}$ | ${-\sqrt{3}}$ | $\frac{-2\sqrt{3}}{3}$ | 2 |
| $180^{0}={\pi}$ | 0 | -1 | 0 | ${\pm\infty}$ | -1 | indet |
| $210^{0}=\frac{7\pi}{6}$ | ${-\frac{1}{2}}$ | ${-\frac{\sqrt{3}}{2}}$ | $\frac{\sqrt{3}}{3}$ | ${\sqrt{3}}$ | ${-\frac{2\sqrt{3}}{3}}$ | -2 |
| $225^{0}=\frac{5\pi}{4}$ | ${-\frac{\sqrt{2}}{3}}$ | ${-\frac{\sqrt{2}}{2}}$ | 1 | 1 | ${-{\sqrt{2}}}$ | ${-{\sqrt{2}}}$ |
| $240^{0}=\frac{4\pi}{3}$ | ${-\frac{\sqrt{3}}{2}}$ | ${-\frac{1}{2}}$ | ${\sqrt{3}}$ | $\frac{\sqrt{3}}{3}$ | -2 | ${-\frac{2\sqrt{3}}{3}}$ |
| $270^{0}=\frac{3\pi}{2}$ | -1 | 0 | ${\pm\infty}$ | 0 | Indet | ${-\infty}$ |
| $300^{0}=\frac{5\pi}{3}$ | ${-\frac{\sqrt{3}}{2}}$ | $\frac{1}{2}$ | ${-\sqrt{3}}$ | ${-\frac{\sqrt{3}}{3}}$ | 2 | ${-\frac{2\sqrt{3}}{3}}$ |
| $315^{0}=\frac{7\pi}{4}$ | ${-\frac{\sqrt{2}}{2}}$ | $\frac{\sqrt{2}}{2}$ | -1 | -1 | ${\sqrt{2}}$ | ${-{\sqrt{2}}}$ |
| $330^{0}=\frac{11\pi}{6}$ | ${-\frac{1}{2}}$ | $\frac{\sqrt{3}}{2}$ | ${-\frac{\sqrt{3}}{3}}$ | ${-{\sqrt{3}}}$ | $\frac{2\sqrt{3}}{3}$ | -2 |
Já podemos exercitar alguma coisa. Vejamos:
01. Um ângulo central, subtendido pelo arco $\widehat{AB}$, de origem no ponto “zero” dos arcos crescentes, mede $\alpha = \frac{27}{4}\cdot\pi\, rad$. Encontre a menor determinação desse ângulo e reduza-o ao primeiro quadrante.
Para resolver essa questão vamos obter a sua expressão na forma geral dos arcos, dividindo a medida por $2\pi$. O maior quociente inteiro nos fornece o valor do $\kappa$, isto é, o número de voltas completas. Cada volta, podemos denominar “ciclo”.
$\alpha = \left(\frac{24}{4}\cdot\pi + \frac{3}{4}\pi\right) rad$
$\alpha = \left(6\pi + \frac{3}{4}\pi\right)\, rad$
$\alpha = {6\pi} + \frac{3}{4}\pi\, rad$
$2\cdot\kappa = 6$$\Leftrightarrow$$\kappa = \frac{6}{2} = 3$
Se: $180^{0} = \pi$
e $ x = \frac{3}{4}\pi$
$\pi\cdot x= 180^{0}\cdot \frac{3\pi}{4}$
$x = 180^{0}\cdot \frac{3\pi}{4\pi} = 135^{0}$
A menor determinação do ângulo é $\frac{3}{4}\cdot\pi\, rad = 135^{0}$
Seu equivalente no primeiro quadrante é
$\pi – \frac{3}{4}\cdot\pi = \frac{4\pi – 3\pi}{4}= \frac{1}{4}\cdot\pi = 45^{0}$
A menor determinação positiva desse arco será um arco de $135^{0}$ e equivale ao arco de $45^{0}$ no primeiro quadrante.
02. Um arco começa na origem dos arcos crescentes e sua extremidade está a $3540^{0}$ desse ponto. Determine: a)a expressão geral dos arcos côngruos; b) a menor determinação do arco; c) o equivalente no primeiro quadrante.
Começamos pela determinação do número de ciclos e da menor determinação positiva.
$\frac{3540^{0}}{360^{0}} = 9 ciclos + 320^{0}$
$\kappa = 9 ciclos$$\Rightarrow$ número de voltas completas.
$\alpha = 320^{0}$$\Rightarrow$ menor determinação positiva do arco.
$\alpha = 9\cdot {360^{0}} + 320^{0} $$\rightarrow$ expressão geral dos arcos côngruos.
03. Verifique se os arcos de medidas $ 6230^{0}$ e $8390^{0}$ são côngruos.
Para fazer esta verificação basta dividir a diferença entre eles por $360^{0}$. Se o quociente for exato, os arcos são côngruos.
$8390^{0} – 6230^{0} = 2160^{0}$$\rightarrow$ diferença.
$\frac{2160^{0}}{360^{0}} = 6$$\rightarrow$ divisão exata.
Os arcos são côngruos.
04. Determinar a localização principal do arco de $4380^{0}$ utilizando a regra prática.
$\frac{4380^{0}}{360^{0}} = 6\cdot{360^{0}} + 60^{0}$
A menor determinação positiva, também denominada principal determinação do arco é $\alpha = 60^{0}$
05. Qual a determinação principal do arco com medida igual a $1190^{0}$?
$\frac{1190^{0}}{360^{0}} = 3\cdot {360^{0}} + 110^{0}$
Menor determinação do arco $\alpha = 110^{0}$
06. Confira se os arcos de medidas $2010^{0}$ e $900^{0}$ são côngruos.
$2010^{0} – 900^{0} = 1110^{0}$
$\frac{1110^{0}}{360^{0}} = 3\cdot{360^{0}} + 30^{0}$
Os arcos não são côngruos, pois a diferença entre suas medidas não é divisível por $360^{0}$.
07. Dado o arco $\frac{17\pi}{4}\, rad$, determine sua menor determinação positiva.
Podemos decompor a expressão do arco em:
$\frac{16}{4}\cdot\pi + \pi\, rad$$\Leftrightarrow$$ 4\cdot\pi + \pi\, rad$
$ \kappa = \frac{4\pi}{2\pi} = 2$
O arco tem dois ciclos completos e a menor determinação positiva é $\alpha = \pi\, rad$
08. Um arco tem a medida de $\gamma = \frac{15\pi}{4}\, rad$. Obtenha a sua menor determinação positiva e escreva a expressão geral dos seus arcos côngruos.
Vamos separar o arco em partes:
$ \frac{8}{4}\cdot\pi + \frac{7\pi}{4}\, rad$$\Leftrightarrow$$ 2\pi + \frac{7}{4}\cdot\pi\, rad$
$\kappa = \frac{2\pi}{2\pi} = 1 $
$\gamma = 1\cdot\pi + \frac{7}{4}\cdot\pi\, rad $
$\alpha = \frac{7}{4}\cdot\pi\, rad$$\rightarrow$ menor determinação positiva do arco.
09. Verifique se os ângulos $\gamma = \frac{25\pi}{3}\, rad$ e $\beta = \frac{37\pi}{3}\, rad$ são côngruos. Escreva a expressão geral dos arcos se forem côngruos.
Calculando a diferença entre eles.
$\beta – \gamma = \frac{37\pi}{3} – \frac{25\pi}{3}\, rad$
$\beta – \gamma = \frac{37\pi – 25\pi}{3} = 12\pi\, rad$
$\kappa = \frac{12\pi}{2\pi} = 6 ciclos$
Os arcos são côngruos e a expressão geral dos mesmos é:
$\zeta = 2\kappa\pi + 1\cdot\pi\, $
Exercícios para resolver.
01. (FEI) Calcule a primeira determinação positiva do conjunto de arcos de mesma extremidade que o arco de medida $\frac{38}{3}\cdot\pi\, rad $
02. (FEI) Quantos são os valores de m compreendidos entre 30 e 40, que tornam côngruos os arcos de medidas $(4m+10).180^{0}$ e $(3m-2).180^{0}$ ?
03. Sendo a medida de um arco 5845^{0}. Determine sua menor determinação positiva e escreva a expressão geral dos arcos côngruos.
04. Um arco mede ${43}{4}\pi\, rad$. Qual é a sua menor determinação positiva? Escreva a expressão geral dos arcos côngruos.
05. Dois arcos medem ${47}{3}\pi\, rad$ e ${33}{5}\pi\, rad$. Determina as menores determinações desses arcos, verifique se são côngruos e escreva as expressões gerais dos arcos côngruos.
Havendo dúvidas, peça ajuda por meio de um dos canais abaixo listados.
Curitiba, 06 de abril de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

