Figuras geométricas.
Ângulos
A intersecção de duas retas ou o encontro de dois segmentos de reta, formam o que chamamos de ângulo. Vejamos a figura ilustrativa abaixo.
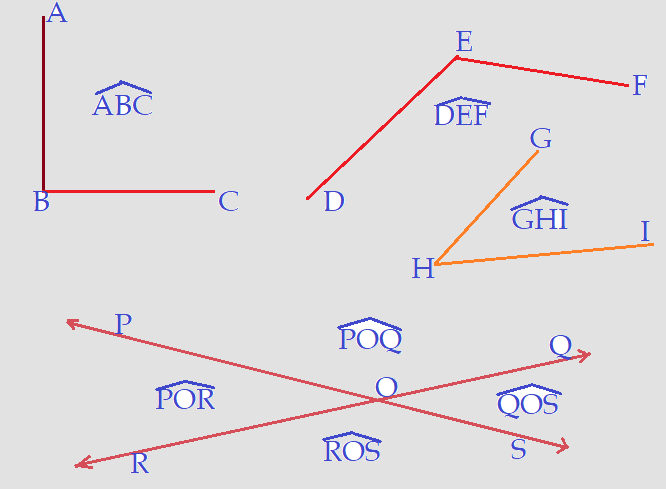
Vértice: – é o ponto de encontro dos segmentos ou das retas que formam o ângulo.
Unidades de ângulos:
a) a unidade mais empregada para medir ângulos é o “grau”. Uma circunferência é dividida em $360^{0}$. Isso equivale a dizer que a divisão da circunferência em quatro partes iguais resulta num ângulo reto que mede $90^{0}$.
b) a partir da expressão do comprimento da circunferência, obtemos outra unidade. Estamos falando do radiano e resulta da divisão do comprimento pelo raio. Disso resulta:
$\frac{2\cdot\pi\cdot R}{R} = 2\pi\,rad$
c)existe uma terceira unidade denominada “grado” e uma circunferência é dividida em 400 gr. Essa unidade é pouco empregada.
Equivalências entre as unidades de ângulos.
Vimos que uma circunferência mede:
$360^{0} = 400 gr = 2\pi\, rad$
Ao dividir a circunferência em quatro partes ficamos com:
$90^{0} = 100 gr = \frac{2\pi}{4} = \frac{\pi}{2}\,rad$
Ao dividir a mesma em duas partes (metades), temos:
$180^{0} = 200 gr = \frac{2\pi}{2} = \pi\,rad$
Classificação de ângulos
Os ângulos são classificados em função das suas medidas nas várias unidades.
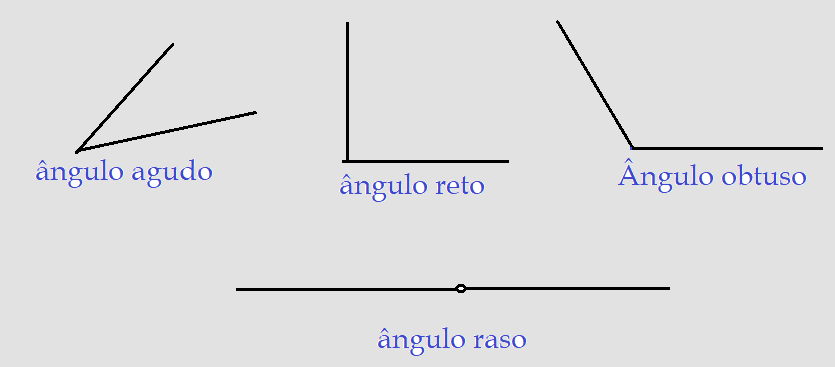
a) Ângulo agudo: – é a denominação dos ângulos menores que $90^{0}$. ( ${0^{0}\lt\alpha\lt{90^{0}}}$)
b)Ângulo reto: – é o ângulo que mede 90^{0} ou o equivalente em radianos ou grados. (${\alpha = 90^{0} = {\pi\over{2} }rad = 100 gr}$)
c)Ângulo obtuso: – é todo ângulo que mede mais do que $90^{0}$. (${90^{0}\lt\alpha\lt 180^{0} = {\pi rad} = 200 gr}$)
d)Ângulo raso: – equivale a meia volta. Seriam duas semi-retas colineares ou segmentos colineares.($\alpha = 180^{0} = {\pi rad} = 200 gr$)
e)Ângulos congruentes ou côngruos: – são ângulos que apresentam a mesma medida (abertura). Podem ser sobrepostos, como se fossem um.
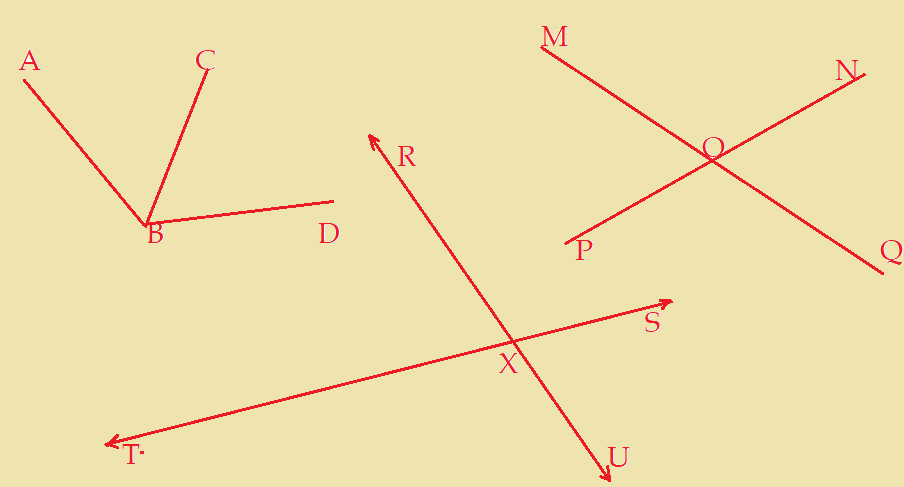
Ângulos em função da posição.
Ângulos adjacentes: – São ângulos que têm um lado comum e o mesmo vértice.
Ângulos opostos pelo vértice: – são ângulos formados por dois pares de segmentos consecutivos ou por duas retas concorrentes. O vértice comum é o ponto de intersecção dos segmentos ou das retas.
Ângulos complementares: – são ângulos que somados completam um ângulo reto, ou seja $90^{0}$.
Ângulos suplementares: – são ângulos que somados totalizam um ângulo raso, isto é, totalizam $180^{0}$.
Ângulos replementares: – são ângulos cuja soma perfaz um ângulo de $270^{0}$. Isso equivale à $\frac{3}{4}$ da circunferência.
Ângulos implementares: – os ângulos que somados completam uma volta, isto é uma circunferência, recebem essa denominação.
Retas paralelas cortadas por uma transversal.
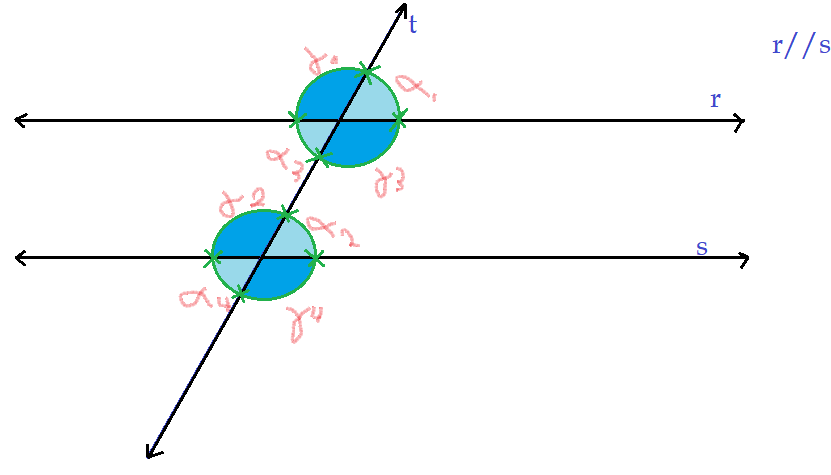
Observando atentamente essa figura, podemos encontrar mais algumas conclusões importantes.
a) Ângulos alternos externos: – são os ângulos externos às retas paralelas e ficam em lados opostos da reta transversal. Assim $\alpha_{1}$ é alterno externo de $\alpha_{4}$; $\gamma_{1}$ é alterno externo de $\gamma_{4}$. Esses ângulos são congruentes entre si.
b)Ângulos alternos internos: – são os ângulos internos às retas paralelas e situados em lados opostos à reta transversal. São alternos externos os ângulos $\alpha_{3}$ e $\alpha_{2}$; $\gamma_{3}$ e $\gamma_{2}$. Também estes são congruentes entre si.
c)Ângulos colaterais externos: – são os ângulos externos às retas paralelas e situados do mesmo lado da reta transversal. Isso nos permite dizer que $\alpha_{1}$ é colateral externo de $\gamma_{4}$ e que $\gamma_{1}$ é colateral externo de $\alpha_{4}$. São ângulos suplementares.
d)Ângulos colaterais internos: – são os ângulos internos às retas paralelas e situados do mesmo lado da reta transversal. Então temos que $\gamma_{3}$ e $\alpha_{2}$, assim como $\alpha_{3}$ e $\gamma_{2}$ são colaterais internos.
Obs.: Facilmente se percebe que os ângulos colaterais, tanto os internos quanto os externos são respectivamente suplementares, isto é, somadas suas medidas resultam 180º.
e)Ângulos correspondentes: – são ângulos que se situam do mesmo lado da reta transversal e estão voltados para o mesmo lado. Se deslizássemos uma das paralelas sobre a outra eles iriam coincidir ou se sobrepor. Em outras palavras, eles são congruentes. Sempre serão um interno e o outro externo.
Feixe de paralelas cortadas por transversais.
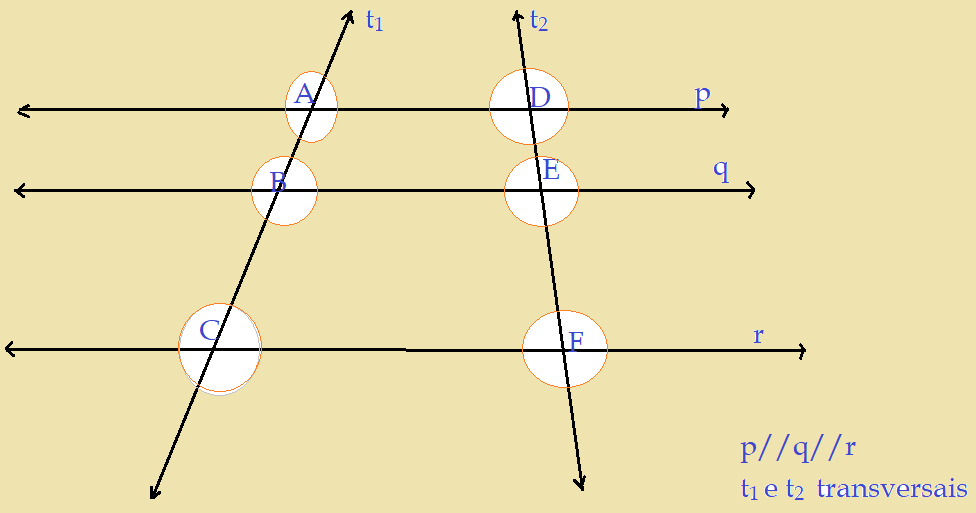
Aqui podemos também identificar todos os ângulos vistos no item anterior. Agora, porém, daremos um passo em frente. Vamos analisar os segmentos de reta determinados pelas paralelas sobre as transversais. Se as transversais também fossem paralelas, haveria a determinação de segmentos congruentes entre as mesmas paralelas. Como não é esse o caso, iremos constatar que existe uma proporcionalidade entre esses segmentos. Quanto mais o ângulo entre as transversais e as paralelas se aproxima de 90º, menor se torna o segmento determinado. Por isso podemos dizer que para ângulos quaisquer, esses mesmos segmentos são proporcionais. Assim:
$\frac{\overline{AB}}{\overline{BC}} = \frac{\overline{DE}}{\overline{EF}}$
Aplicando as propriedades das proporções podemos mudar a ordem dos segmentos e escrever de outra forma.
$\frac{\overline{AB}}{\overline{DE}} = \frac{\overline{BC}}{\overline{EF}}$
Mantendo o mesmo raciocínio também é válido dizer que:
${{\overline{AB}\over\overline{AC}} = {\overline{DE}\over\overline{EF}}}$
Divisão áurea ou extrema razão.
Se um segmento de reta $\overline{AC}$ for dividido em dois segmentos por um ponto $B$, de modo que se tenha:
$\frac{\overline{AC}}{\overline{AB}} = \frac{\overline{AB}}{\overline{BC}}$
Vejamos a figura:
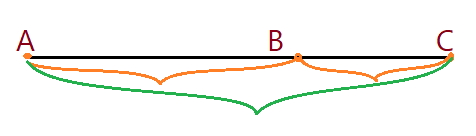
Fazendo: $\Phi = \frac{\overline{AC}}{\overline{AB}} = \frac{\overline{AB}}{\overline{BC}}$
$\Phi = \frac{\overline{BC} + \overline{AB}}{\overline{BC}}$
$\Phi = \frac{\overline{BC}}{\overline{BC}} + \frac{\overline{AB}}{\overline{BC}}$
$\Phi = 1 + \frac{\overline{BC}}{\overline{AB}}$$\Leftrightarrow$$\Phi = 1 + \frac{1}{\Phi}$
${\Phi}^{2} = \Phi + 1$$\Leftrightarrow$${\Phi}^{2} – \Phi – 1 = 0$
Resolvendo a equação do segundo grau:
$\Delta = (-1)^{2} – 4\times 1\times {(-1)} = 5$
$\Phi = \frac{-(-1)\pm\sqrt{5}}{2\times 1}$
$\Phi_{1} = \frac{1 + \sqrt{5}}{2}$
$\Phi_{2} = \frac{1 – \sqrt{5}}{2}$
Desprezamos a raiz que terá valor negativo e ficamos com um valor
$\Phi = \frac{1 + \sqrt{5}}{2}$$\Leftrightarrow$$\color{Navy}{\Phi = 1,618033989…}$
Via de regra usamos até a terceira casa decimal: $\color{Maroon}{1,618}$
Este é o valor da razão áurea ou média e extrema razão.
Que tal um pouco de exercícios!
- Exprimir um ângulo de $135^{0}$ nas unidades radiano e grado.
Sabemos que ; $180^{0} = \pi\,rad$,
Isso nos permite escrever: $\frac{180^{0}}{135^{0}} = \frac{\pi}{x}$$\Leftrightarrow$$x = \frac{135^{0}}{180^{0}}\cdot\pi$
$x = \frac{3}{4}\cdot\pi\, rad$
Se ${360^{0} = 400 gr}$$\Leftrightarrow$$\frac{360^{0}}{135^{0}} = \frac{400}{x}$
$ x = 400\cdot\frac{135^{0}}{360^{0}}$$\Leftrightarrow$
$x = 150\,gr$
Resposta: $135^{0} = 150\,gr = \frac{3}{4}\cdot\pi\,rad$
2. Determinar o complemento, o suplemento, o replemento e o implemento de um ângulo de ${\pi\over{3}}rad$.
a) complemento
$x + \frac{\pi}{3} = \frac{\pi}{2}$
$x = \frac{\pi}{2} – \frac{\pi}{3}$$\Leftrightarrow$$x = \frac{3\pi – 2\pi}{6}$
$x =\frac{\pi}{6}\,rad$
b) suplemento
$ x + \frac{\pi}{3} = \pi$$\Leftrightarrow$$x = \pi – \frac{\pi}{3}$
$x =\frac{3\cdot\pi -\pi}{3}$$\Leftrightarrow$$x = \frac{2\pi}{3}\,rad$
c) replemento
$x + \frac{\pi}{3} = \frac{3\pi}{2}$
$x = \frac{3\pi}{2} – \frac{\pi}{3}$
mmc(3 e 2) = 6
$x =\frac{3\cdot{3\pi} – 2\cdot\pi}{6}$$\Leftrightarrow$$x = \frac{9\pi – 2\pi}{6} = \frac{7\pi}{6}\,rad$
d)implemento
$x +\frac{\pi}{3} = 2\pi$$\Leftrightarrow$$x = 2\pi – \frac{\pi}{3}$
$x = \frac{3\cdot{2\pi} – \pi}{3}$$\Leftrightarrow$$x = \frac{6\pi – \pi}{3}$ $\Leftrightarrow$$x = \frac{5\pi}{3}\,rad$
3. Um ângulo $\alpha = \frac{\pi}{4}\,rad$, é formado por duas retas concorrentes no ponto ${P}$. Pede-se determinar a medida do seu ângulo oposto pelo vértice e as medidas dos dois ângulos adjacentes formados pelas mesmas retas.
O ângulo oposto pelo vértice, como vimos, é congruente ao ângulo dado. Portanto: $\alpha_{1} = \frac{\pi}{4}\,rad$.
Os ângulos adjacentes são os suplementos do ângulo dado e são congruentes entre si, pois também são opostos pelo vértice por sua vez. Então:
$\beta + \frac{\pi}{4} = \pi $$\Leftrightarrow$$\beta = \pi – \frac{\pi}{4}$
$\beta = \frac{4\pi – \pi}{4}$$\Leftrightarrow$$\beta = \frac{3\pi}{4}\,rad$
Os dois ângulos adjacentes são congruentes e portanto têm a mesma medida.
4. Um feixe de três retas paralelas (r//s//p), é cortado por duas retas transversais $t_{1}$ e $t_{2}$, determinando sobre $t_{1}$, os segmentos $\overline{AB} = 5,0\,cm$ e $\overline{AC} =12,0\,cm$. Na reta $t_{2}$ fica determinado o segmento $\overline{DF} = 15,0 \,cm$. Pede-se determinar os segmentos $\overline{BC}$, $\overline{DE}$ e $\overline{EF}$.
Pela lógica do exercício, pode-se escrever:
$\overline{AB} + \overline{BC} = \overline{AC}$
$\overline{BC} = \overline{AC} – \overline{AB}$
$\overline{BC} = \overline{AC} – \overline{AB}$
A proporção fica:
$\frac{\overline{AB}}{\overline{AC}} = \frac{\overline{DE}}{\overline{DF}}$
$\frac{5,0}{12,0} = \frac{\overline{DE}}{15,0}$
$\frac{{5,0}\cdot{15,0}}{12,0} = \overline{DE}$
$\overline{DE} = 6,25\,cm$
Para o segmento $\overline{EF}$
$\overline{DE} + \overline{EF} = \overline{DF}$
$\overline{EF} = \overline{DF} – \overline{DE}$
$\overline{EF} = 15,0 – 6,25 = 8,75\,cm$
5. Determine o segmento que divide o segmento $\overline{AC} = 10\,cm$ em dois segmentos segundo a divisão áurea.
$\Phi = \frac{\overline{AC}}{\overline{AB}}$
$\overline{AB} =\frac{\overline{AC}}{\Phi}$$\Leftrightarrow$$\overline{AB} = \frac{10}{1,618}$
$\overline{AB}\simeq 6,180\,cm$
$\overline{BC} = \overline{AC} – \overline{AB}$$\Leftrightarrow$$\overline{BC} = 10 – 6,180$
$\overline{BC}\simeq 3,82\,cm$
6. Determine a medida dos segmentos que formam os segmentos que estão entre si na razão áurea, maiores que $c = 7,0\,cm$.
$\Phi = \frac{b}{c}$$\Leftrightarrow$$1,618 = \frac{b}{7,0}$
$b = \Phi\times 7$$\Leftrightarrow$$b = 1,618\times 7,0$
$\color{Sepia}{b = 11,326\,cm}$
$\Phi = \frac{a}{11,326}$$\Leftrightarrow$$a = 1,618\times 11,326$
$\color{Sepia}{a = 18,326\,cm}$
Agora é a sua vez.
- Determine os suplementos dos ângulos ${\alpha = 30^{0}}$, ${\beta = 75^{0}}$, ${\theta = 120^{0}}$. Exprima os valores também em radianos.
- Determine os replementos dos ângulos ${\epsilon ={ 2\pi\over{3}}}$, ${\gamma = {3\pi\over{4}}}$, ${\omega = {\pi\over{6}}}$. Exprima os resultados também em graus.
- Determine o implemento dos ângulos ${\alpha = 150^{0}}$, ${\gamma = 225^{0}}$ e ${\beta = 45^{0}}$. dê os resultados também em radianos e grados.
- Dois ângulos adjacentes formam juntos um ângulo raso. Se a medida de um deles é igual a $\frac{1}{3}$ desse ângulo, quanto mede o outro? Exprima os valores em graus, grados e radianos.
- Uma reta transversal intercepta duas paralelas, formando um ângulo obtuso de ${135^{0}}$. Quanto mede o ângulo colateral agudo desse ângulo? Exprima os resultados nas outras unidades.
- Duas retas transversais interceptam um feixe de paralelas, determinando sobre a primeira transversal os segmentos ${\overline{MN} = 7,0cm}$, ${\overline{NO} = 9,0 cm}$ e na outra transversal o segmento ${\overline{PQ} = 6,0 cm}$. Determine os segmentos ${\overline{MO}}$, ${\overline{PR}}$ e ${\overline{QR}}$.
- Um segmento de $15\,cm$ é dividido em dois segmentos que formam com ele uma razão áurea. Determine as medidas desses segmentos.
- Em um conjunto de três segmentos em uma razão áurea o segmento de medida entre o maior e o menor tem $b = 8,0\,cm$. Determine as medidas dos outros dois segmentos.
Havendo dificuldades faça contato comigo para esclarecimentos. Os canais são estes relacionados abaixo.
Curitiba, 24 de outubro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

