Relação de pertinência.
Pertence/não pertence
Para dizer que um determinado elemento faz parte ou não de um conjunto, usamos as palavras pertence e não pertence. Simbolicamente, usamos $\in$ e $\notin$.
Assim, dado o conjunto das vogais:
$V = {a, e, i, o, u}$ podemos dizer que:
- $a\in V$$\Rightarrow$ “a pertence ao conjunto V”;
- $i\in V$$\Rightarrow$ “ i pertence ao conjunto V“;
- $u\in V$$\Rightarrow$”u pertence ao conjunto V”;
- $m\notin V$$\Rightarrow$ “m não pertence ao conjunto V”;
- $r\notin V$$\Rightarrow$ “r não pertence ao conjunto V”;
e assim sucessivamente.
Subconjunto
Tomemos por exemplo o conjunto das vogais.
- $\bbox[4px,border:2px solid Olive]{\color{Navy}{ A = \{a, e, i, o, u\}}} $
Denominamos sub-conjunto de um conjunto dado, a todo conjunto cujos elementos pertençam a este conjunto. No exemplo acima, conjunto das vogais, temos 5 (cinco) elementos. Vimos que existe o conjunto vazio, que não tem nenhum elemento; conjunto unitário com um elemento apenas e assim por diante. Iremos formar um conjunto de subconjuntos do conjunto $\color{Navy}{A}$, também denominado conjunto das partes. Vejamos detalhadamente.
- $\color{Navy}{ A’_{1} = ∅ ou \{ \}} $
- $\color{Navy}{ A’_{2} = \{a\}}$
- $\color{Navy}{ A’_{3} = \{e\}} $
- $\color{Navy}{ A’_{4}= \{i\}} $
- $\color{Navy}{ A’_{5}= \{o\}} $
- $\color{Navy}{ A’_{6}= \{u\}} $
- $\color{Navy}{ A’_{7}= \{a, e\}} $
- $\color{Navy}{ A’_{8}= \{a, i\}} $
- $\color{Navy}{ A’_{9}= \{a, o\}} $
- $\color{Navy}{ A’_{10}= \{a, u\}} $
- $\color{Navy}{ A’_{11}= \{e, i\}} $
- $\color{Navy}{ A’_{12}= \{e, o\}} $
- $\color{Navy}{ A’_{13}= \{e, u\}} $
- $\color{Navy}{ A’_{14}= \{i, o\}} $
- $\color{Navy}{ A’_{15}= \{i, u\}} $
- $\color{Navy}{ A’_{16}= \{o, u\}} $
- $\color{Navy}{ A’_{17}= \{a, e, i\}} $
- $\color{Navy}{ A’_{18}= \{a, e, o\}} $
- $\color{Navy}{ A’_{19}= \{a, e, u\}} $
- $\color{Navy}{ A’_{20}= \{a, i, o\}} $
- $\color{Navy}{ A’_{21}= \{a, i, u\}} $
- $\color{Navy}{ A’_{22}= \{a, o, u\}} $
- $\color{Navy}{ A’_{23}= \{e, i, o\}} $
- $\color{Navy}{ A’_{24}= \{e, i, u\}} $
- $\color{Navy}{ A’_{25}= \{e, o, u\}} $
- $\color{Navy}{ A’_{26}= \{i, o, u\}} $
- $\color{Navy}{ A’_{27}= \{a, e, i, o\}} $
- $\color{Navy}{ A’_{28}= \{a, e, i, u\}} $
- $\color{Navy}{ A’_{29}= \{a, e, o, u\}} $
- $\color{Navy}{ A’_{30}= \{a, i, o, u\}} $
- $\color{Navy}{ A’_{31}= \{e, i, o, u\}} $
- $\color{Navy}{ A’_{32}= \{a, e, i, o, u\}} $
NOTA: Todo conjunto é sub-conjunto de si mesmo.
Para um conjunto $\color{Navy}{A}$, vazio, ou sem nenhum elemento:
- $$\color{Navy}{A =\emptyset}$$
- $$\color{Navy}{A’_{1} = \emptyset}$$
Vejamos um exemplo de um conjunto $\color{Navy}{B}$,com apenas um elemento:
- $$\color{Navy}{B = \{m\}} $$
- $$\color{Brown}{ B’_{1} = Ø = \{ \}} $$
- $$\color{Brown}{ B’_{2} = \{m\}} $$
Um conjunto$\color{Navy}{C}$, com dois elementos:
- $$\color{Navy}{ C = \{ m, n\}} $$
- $$\color{Brown}{ C’_{1} = ∅ = \{ \}} $$
- $$\color{Brown}{ C’_{2} = \{m\}} $$
- $$\color{Brown}{ C’_{3} = \{n\}} $$
- $$\color{Brown}{C’_{4} = \{m, n\}} $$
Um conjunto $\color{Navy}{D}$, com três elementos:
- $$\color{Navy}{D = {\{ i, j, k \}}}$$
- $$\color{Brown}{D’_{1} =\emptyset =\{ \}}$$
- $$\color{Brown}{D’_{2} =\{ i \}} $$
- $$\color{Brown}{D’_{3} = \{ j \}} $$
- $$\color{Brown}{D’_{4} = \{ k \}} $$
- $$\color{Brown}{D’_{5} = \{ i, j \}} $$
- $$\color{Brown}{D’_{6} = \{ i, k \}}$$
- $$\color{Brown}{D’_{7} = \{ j, k \}} $$
- $$\color{Brown}{D’_{8} = \{ i, j, k \}} $$
Conjunto $\color{Navy}{E}$ tem 4 elementos:
- $$\color{Navy}{E = \{ a, b, c, d \}}$$
- $$\color{Maroon} {E’_{1} = ∅ = \{ \}}$$
- $$\color{Maroon} {E’_{2} =\{ a \}}$$
- $$\color{Maroon} {E’_{3} = \{ b \}}$$
- $$\color{Maroon} {E’_{4} = \{ c \}}$$
- $$\color{Maroon} {E’_{5} = \{ d \}}$$
- $$\color{Maroon} {E’_{6} = \{ a, b \}}$$
- $$\color{Maroon} {E’_{7} = \{ a, c \}}$$
- $$\color{Maroon} {E’_{8} = \{ a, d \}}$$
- $$\color{Maroon} {E’_{9} = \{ b, c \}}$$
- $$\color{Maroon} {E’_{10} = \{ b, d \}}$$
- $$\color{Maroon} {E’_{11} = \{ c, d \}} $$
- $$\color{Maroon} {E’_{12}= \{ a, b, c,\}} $$
- $$\color{Maroon} {E’_{13} = \{ a, b, d \}}$$
- $$\color{Maroon} {E’_{14} = \{ b, c, d \}} $$
- $$\color{Maroon} {E’_{15} = \{ a, c, d \}}$$
- $$\color{Maroon} {E’_{16} = \{ a, b, c, d \}}$$
Vejamos agora. O conjunto vazio tem um sub-conjunto. O conjunto de um elemento, tem dois sub-conjuntos. O conjunto com dois elementos, tem quatro sub-conjuntos. O conjunto de 3 elementos, tem 8 sub-conjuntos. O conjunto com 4 elementos, tem 16 sub-conjuntos e o de 5 elementos tem 32 subconjuntos. É notável que, o número de subconjuntos:
n’={ 1, 2, 4, 8, 16, 32,…}
Todos eles são potências de 2. Vejamos:
- $\color{Blue}{2^{0} = 1}$
- $\color{Blue}{2^¹ = 2}$
- $\color{Blue}{2^{2} = 4}$
- $\color{Blue}{2^{3} = 8}$
- $\color{Blue}{2^{4} = 16}$
- $\color{Blue}{ 2^{5} = 32}$
De onde podemos concluir que a quantidade de sub-conjuntos de qualquer conjunto é sempre uma potência de 2, cujo expoente é igual ao número de elementos do conjunto.
Por exemplo, um conjunto de 7 elementos, terá $\color{Blue}{2^{7} = 128}$.
- Podemos concluir que o número de sub-conjuntos de um conjunto com $\color{Navy}{n}$ elementos, é igual potência de base $\color{Navy}{2}$ e expoente $\color{Navy}{n}$.
- $\color{DarkGreen}{n(A) = n }$$\Leftrightarrow$${n'(A’) = 2^n}$
- Todos os sub-conjuntos de um conjunto dado, formam o conjunto das partes do conjunto dado.
Num Diagrama de Venn fica assim:
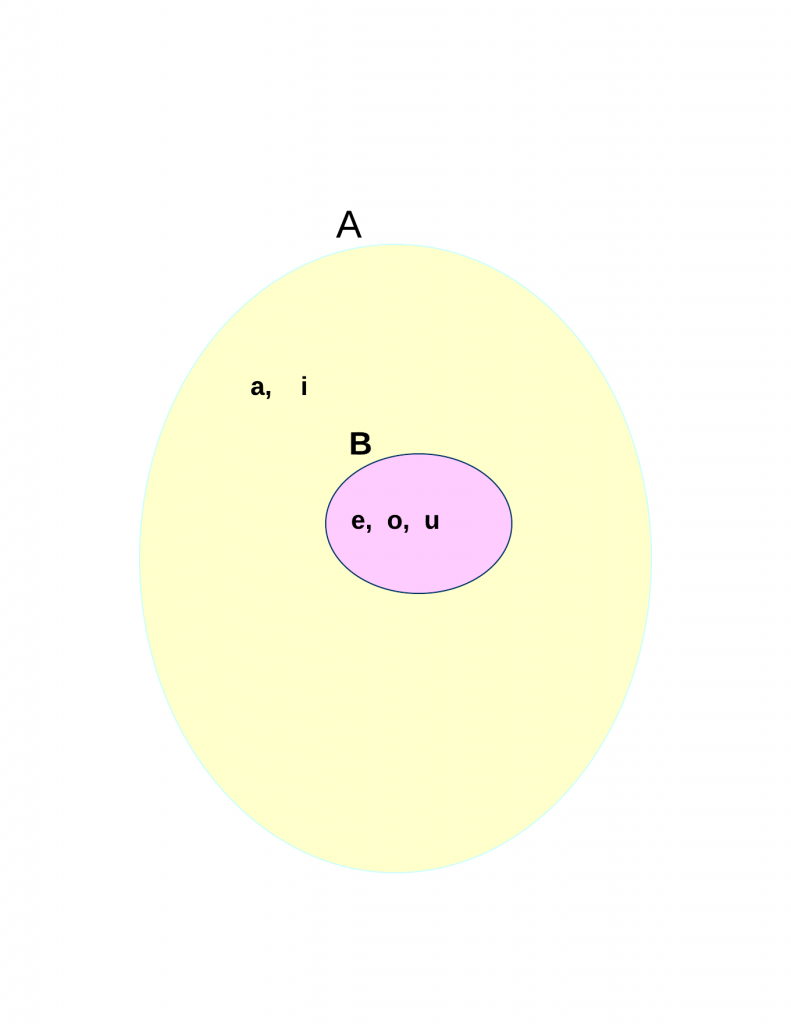
Dizemos que o conjunto contém cada um de seus subconjuntos e cada subconjunto está contido no conjunto de origem.
Está contido: $\mathbf{\color{Sepia}{\subset}}$
Não está contido: $\mathbf{\color{Sepia}{\not\subset}}$
Contém: $\mathbf{\color{Sepia}{\supset}}$
Não contém: $\mathbf{\color{Sepia}{\not\supset}}$
- Vamos ver alguns exemplos.
- $\color{Navy}{\{a, b, c, d, e \} \supset \{a, c, e \}}$
- $\color{Navy}{\{a, b, c \} \subset \{a, b, c, d, e \}}$
- $\color{Navy}{\{ \} \subset \{a, b, c, d, e\}}$
- $\color{Navy}{\{ d \} \subset \{ a, b, c, d, e\}}$
- $\color{Navy}{\{a, b, c, d, e\} \supset\{b, c\}}$
- Escreva o conjunto dos subconjuntos ou conjunto das partes, dos conjuntos abaixo.
- $\color{Navy}{A = \{ 1, 2, 3\}}$
- $\color{Navy}{B = \{ n, p, q, r\}}$
- $\color{Navy}{C = \{ x, y \}}$
- $\color{Navy}{D = \{ t, u, v, x \}}$
- Complete com os símbolos $\color{Navy}{\supset, \not\supset, \subset, \not\subset}$ entre os conjuntos.
- ${\{ \} ……. \{x, y, z \}}$
- ${\{ c, d \} ……..\{ a, b, c, d, e \}}$
- ${\{ m \} …….. \{ l, m, n, o, p\}}$
- ${\{ 1, 3, 5, 7, 9 \} ……. \{ 3, 7 \}}$
- ${\{ garfo, faca, colher, colherinha\} …… \{garfo\}}$
- ${\{ xícara \} ……..\{ prato, xícara, tigela, sopeira \}}$
Curitiba, 06 de julho de 2016 (Revisão e atualização em 04/11/2017).
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

