Operações com conjuntos.
-
União ou reunião de conjuntos.
Sejam:
- $\color{Navy}{A = \{a,e,i,o,u\}}$ $\rightarrow$ conjunto das vogais.
- $\color{Navy}{B = \{a,b,c,d,e,…,x,y,z\}}$$\rightarrow$ alfabeto latino.
A união ou reunião desses dois conjuntos, formará o conjunto das letras do alfabeto. Simbolicamente representamos isso da seguinte maneira:
- $\color{Navy}{A \cup B = U =\{a,b,c,d,e,f,g,…,x,y,z\}}$
- Vemos que ao unir um conjunto a um de seus sub-conjuntos, o resultado é o próprio conjunto.
Num Diagrama de Venn:
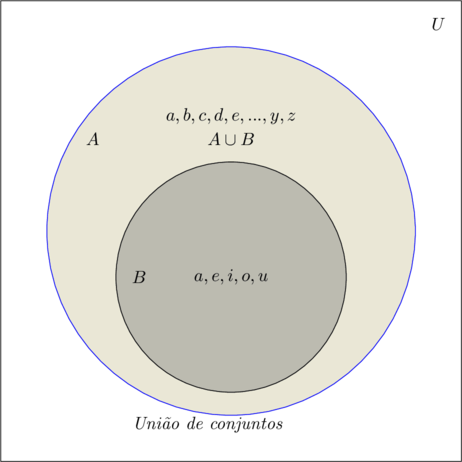
Vejamos outros exemplos:
- $$\color{Maroon}{ M = \{0,1,2,3\}}$$
- $$\color{Maroon}{N = \{3,4,5,6\}}$$
- $$\color{Navy}{M\cup N = \{0,1,2,3,4,5,6,\}}$$
Num Diagrama de Venn
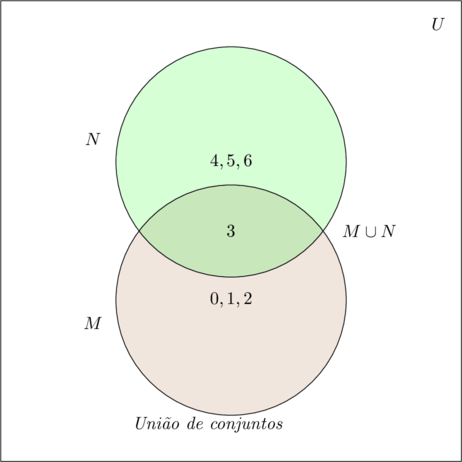
Notamos que o elemento comum aos dois conjuntos, na reunião aparece somente uma vez. No primeiro exemplo, os elementos do conjunto A são todos também elementos do conjunto B e portanto o número de elementos do conjunto união é igual ao número de elementos do conjunto B. No segundo exemplo, temos um elemento comum e assim o conjunto união tem um elemento a menos do que a soma do número de elementos dos conjuntos M e N.
Se os conjuntos a serem unidos, não contiverem elementos comuns, bastará reunir todos os elementos em um único e teremos o conjunto união ou reunião. Vejamos os conjuntos:
- $\color{Navy}{A=\{-4,-2,0,2,4\}}$
- $\color{Navy}{B=\{-3,-1,1,3\}}$
- $\color{Maroon}{A\cup B=\{-4,-3,-2,-1,0,1,2,3,4\}}$
Notamos que o número de elementos $\color{Blue}{n(A\cup B) = n(A) + n(B) = 4 + 5 = 9}$
Num Diagrama de Venn, teremos:
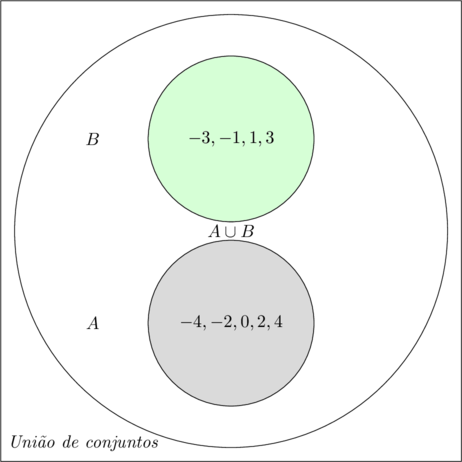
-
Intersecção de conjuntos.
Como vimos nos exemplos anteriores, os conjuntos podem ter elementos comuns entre si. A este conjunto de elementos, que pertencem tanto a um quanto a outro conjunto, denominamos intersecção. Sejam os conjuntos:
- $\color{Brown}{ P = \{a,b,c,d,e\}}$
- $\color{Brown}{ Q = \{a,e,i,o,u\}}$
Entre os dois conjuntos, temos dois elementos comuns. A intersecção é representada simbolicamente pelo símbolo $\color{Navy}{\cap}$. Portanto podemos escrever:
- $$\color{Navy}{P\cap Q = \{a,e\}}$$
Num Diagrama de Venn
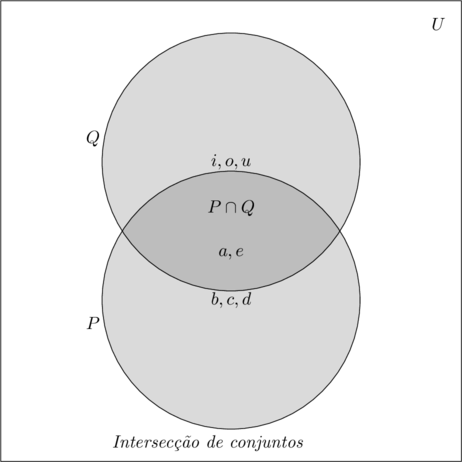
Ou
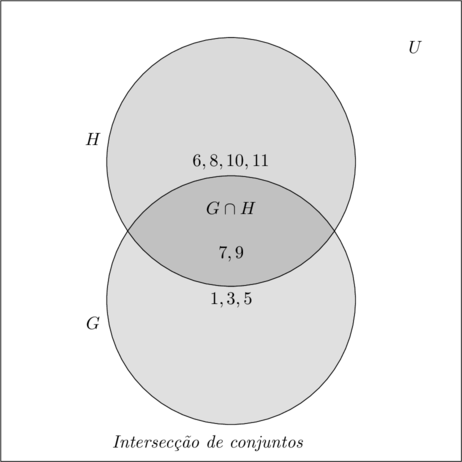
- $\color{Brown}{ G = \{1,3,5,7,9\}}$
- $\color{Brown}{ H = \{6,7,8,9,10,11\}}$
A intersecção fica assim:
- $\color{Navy}{G\cap H = \{7,9\}}$
No Diagrama de Venn
-
Conjuntos disjuntos
O prefixo “dis” indica separação. Desse modo fica fácil compreender que estes conjuntos não tem elementos em comum, isto é, sua intersecção é um conjunto vazio. Podemos retomar o terceiro exemplo da união de conjuntos.
- $\color{Navy}{A = \{-3,-1,1,3\}}$
- $\color{Navy}{B = \{-4,-2, 0, 2,4\}}$
- $\color{Maroon}{A\cap B = \varnothing =\{\}}$

-
Intersecção de mais de dois conjuntos.
- Podemos ter a intersecção entre vários conjuntos, pois um ou mais elementos podem fazer parte de todos eles. Sejam os conjuntos:
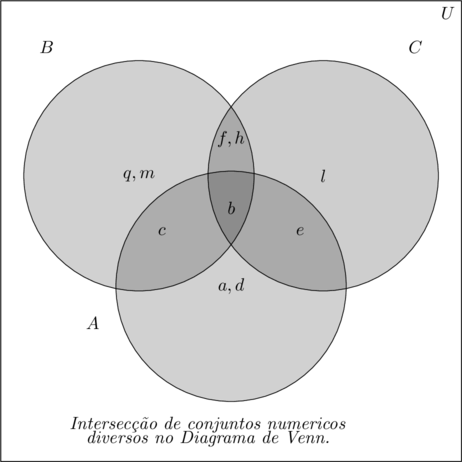
- $\color{Maroon}{A = \{a,b,c,d,e\}}$
- $\color{Maroon}{B = \{b,c,f,g,h,m\}}$
- $\color{Maroon}{C = \{b,e,f,h,l\}}$
- $\color{Navy}{A\cap B = \{b,c\}}$
- $\color{Navy}{B\cap C = \{b,f,h\}}$
- $\color{Navy}{A\cap C = \{b,e\}}$
- $\color{Navy}{A\cap B\cap C = \{b\}}$
Num diagrama de Venn, isso fica assim:
Exercitando um pouco.
- Dados os conjuntos:
- $\color{Navy}{A = \{-10, -5, 0, 5, 10, 15\}}$
- $\color{Navy}{B = \{-2,-1,0,1,2,3\}}$
- $\color{Navy}{C = \{0,2,4,6,8\}}$
- $\color{Navy}{D = \{-1,0,1,3,5,7\}}$
- $\color{Navy}{E = \{2,4,6,8,10,12\}}$
- $\color{Navy}{F = \{1,2,3,4,5\}}$
- $\color{Navy}{G = \{1,5,9,13,17\}}$
- Efetue as operações com os conjuntos e represente-as em Diagrama de Venn.
- $\color{Brown}{A \cup C =\{…\}}$
- $\color{Brown}{B\cap F = \{…\}}$
- $\color{Brown}{C\cup D\cup F =\{…\}}$
- $\color{Brown}{E\cup A\cup D =\{…\}}$
- $\color{Brown}{(A \cup D)\cap (F\cup E) = \{…\}}$
- $\color{Brown}{(B\cap C)\cup (E\cap F) = \{…\}}$
- $\color{Brown}{A\cap (D\cup F) = \{…\}}$
Curitiba, 07 de julho de 2016. Corrigido e atualizado em 04/11/2017 para republicação.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

