fevereiro 2020 – Matemática

15 de fevereiro de 202028 de maio de 2020

Matemática – Geometria. Geometria plana.

Circunferência e círculo

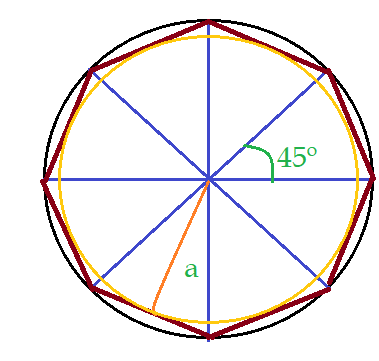
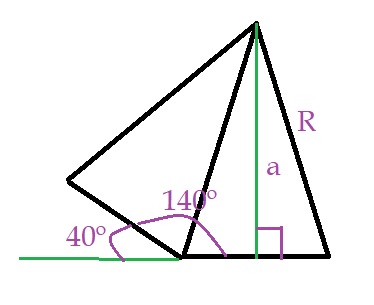
Acabamos de estudar os polígonos regulares e neles foi possível observar que, na medida em que aumenta o número de lados, a forma do polígono torna-se mais arredondada. Inclusive a circunferência inscrita e circunscrita têm a medida de seus raios cada vez mais próximos um do outro. Por essa razão, quando o número de lados tende para o infinito, passamos a ter uma figura denominada circunferência.

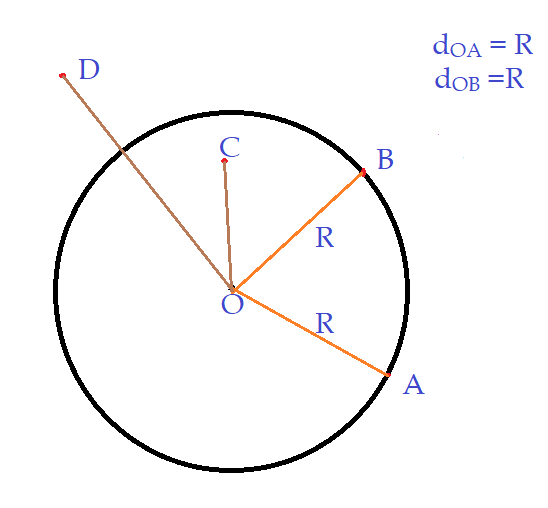
Para simplificar, definimos a circunferência como sendo a figura $\lambda(O,R)$ onde o ponto $O$ é o centro e $R$ é a medida do raio. Dessa forma a circunferência é uma linha poligonal fechada, cujos pontos estão todos a uma distância $R$ do ponto $O$.

Os pontos A e B, estão ambos situados a distância $R$ do centro $O$. Por isso dizemos que eles fazem parte da circunferência.

$d_{OA} = R \land d_{OB} = R$$\Leftrightarrow$$d_{OA} = d_{OB}$

Já os pontos $C \land D$, não pertencem à circunferência, pois:

$d_{OC} \lt R$$\Rightarrow$ ponto interior.

$d_{OD}\gt R$$\Rightarrow$ ponto exterior.

Círculo

É frequente confundirmos círculo e circunferência. Como acabamos de ver, a circunferência é a linha poligonal fechada, ou seja, é o perímetro da figura plana, que denominamos círculo.

Assim podemos afirmar que o círculo é uma área plana, limitada por uma circunferência de mesmo raio.

Observemos a figura ao lado. É um círculo, pois tem o perímetro que é uma circunferência e todos os pontos interiores fazem parte da figura.

Comprimento da circunferência:

Houve muitos matemáticos que se empenharam em determinar uma forma de calcular o comprimento da linha perimetral do círculo, ou seja, a sua circunferência. Após muitas tentativas, chegou-se a uma aproximação aceita universalmente, tendo inclusive determinados os algarismos decimais em muitos milhares. O resultado é um número irracional $\pi$, que resulta da divisão do comprimento da circunferência pela medida do raio. As maiores dificuldades residem na determinação, com o máximo de precisão possível dessas medidas.

$C = 2\cdot\pi\cdot R$

Diâmetro

É o dobro da medida do raio. É em verdade uma corda que passa pelo centro. Por isso:

$D = 2\cdot R$

$C = D\cdot\pi$

Área do círculo

Para determinar a área de um círculo usamos a expressão: $A = \pi\cdot R^2$

Sendo $D = 2R$$\Leftrightarrow$$R = {D\over 2}$

$A = \pi\cdot\left(\frac{D}{2}\right)^{2} = \frac{\pi\cdot D^{2}}{4}$

Semi-círculo e arco de circunferência.

Um diâmetro divide o círculo ao meio. Cada metade denominamos semi-círculo. Veja a parte em verde na figura que segue.

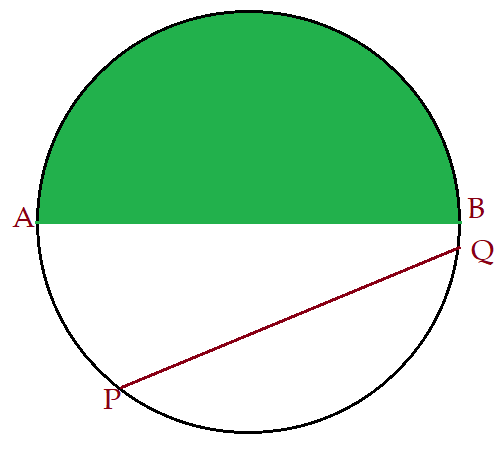
Qualquer segmento de reta traçado entre dois pontos da circunferência, sem passar pelo centro, é uma corda. Como podemos ver na figura ao lado. Os pontos compreendidos entre os pontos $P$ e $Q$ da corda, formam um arco de círculo. Do mesmo modo também os pontos da circunferência que fazem parte do semi-círculo, são um arco de círculo. Neste caso trata-se de meia circunferência.

Setor circular

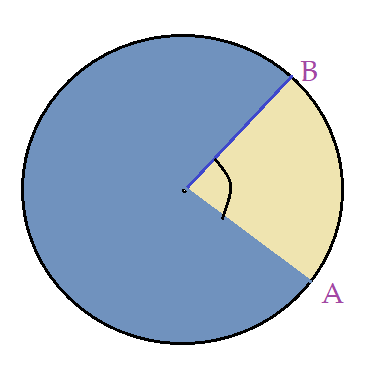
Se você já cortou uma “pizza” circular, retirando uma “fatia”, essa mesma é um exemplo de setor circular. Veja na figura ao lado. Podemos calcular a área do setor circular, bastando que tenhamos a medida do ângulo formado pelos lados do setor.

Digamos que a fatia retirada tenha a medida de um ângulo de $60^{0}$ ou seja $\frac{\pi}{3}$.

Se dividirmos a área do círculo em partes iguais, cada uma a $\pi\, rad$ e multiplicarmos pelo ângulo da fatia, teremos a área da mesma.

$A_{S} = \frac{\pi\cdot R^{2}}{2\pi}\cdot \frac{\pi}{3}$

$A_{S} = \frac{\pi\cdot R^{2}}{6}$

Ficaria faltando apenas a medida do raio do círculo.

Ângulo central é o ângulo de um setor circular. O vértice fica no centro do círculo.

Vale lembrar que o resto do círculo também será um setor circular.

Coroa circular

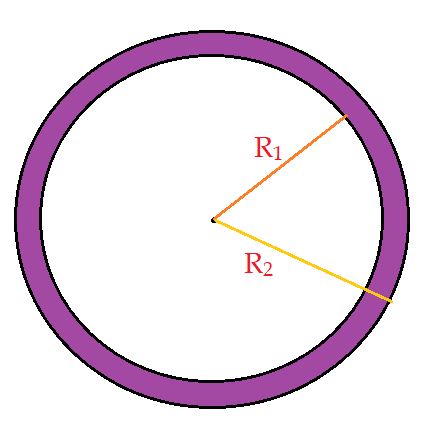
Forma-se uma coroa circular se cobrirmos um círculo maior, por um outro, pouco menor que o primeiro, de modo que os centros fiquem coincidentes. Ficará aparecendo apenas uma estreita faixa do primeiro. É essa faixa que denominamos coroa circular.

A área da coroa circular é a diferença entre as áreas dos dois círculos sobrepostos, o que pode ser resumido assim:

$A_{cor}= {\pi\cdot {R_{2}}^{2} – \pi\cdot{R_{1}^{2}}}$

$A_{cor}= \pi\cdot\left({{R_{2}}^{2}-{R_{1}^{2}}}\right)$

Exercícios

01. A respeito da definição básica das circunferências e de suas propriedades, assinale a alternativa correta.

( )a) uma circunferência é uma região plana limitada por um círculo;

( )b) uma circunferência é um conjunto de pontos cuja distância até o centro é sempre menor do que a constante r;

( )c) uma circunferência possui apenas dois raios e a soma desses dois elementos é igual ao diâmetro;

( )d) uma circunferência de centro O e raio r é um conjunto de todos os pontos cuja distância até O é igual a r;

( )e) círculo é a região do plano limitada por um diâmetro.

02. Dada uma circunferência de centro O e raio r, assinale a alternativa correta:

( )a) dado um ponto A, fora da circunferência, o segmento OA é menor ou igual a r;

( )b) sabendo que $\overline{OA}$ tem comprimento menor do que $r$, pode-se afirmar que A pertence ao círculo limitado por essa circunferência;

( )c) sabendo que $\overline{OA}$ tem comprimento maior do que $r$, pode-se afirmar que A pertence à circunferência;

( )d) o diâmetro do círculo limitado por essa circunferência é igual a $3r$;

( )e) para que o ponto A pertença à circunferência, basta que a distância $\overline{AO}$ seja menor do que $r$.

03. Determinar o diâmetro e a área de um círculo (respectivamente), cujo perímetro mede 36π cm.

( )a) $63,0\, cm \land 300\pi\,cm^{2}$;

( )b) $36,0\, cm \land 324\pi\,cm^{2}$;

( )c) $50,0\, cm \land 324\pi\, cm^{2}$;

( )d) $36,0\, cm \land 300\pi\, cm^{2}$;

( )e) $43,0\, cm \land 324\pi\,cm^{2}$.

04. A roda de um automóvel tem um diâmetro que mede $D =50\, cm$. Determine a distância percorrida por esse veículo após uma de suas rodas completar 1750 voltas. Adotar$\pi = 3,14$ e supor que a roda não deslize durante a rolagem.

( )a) 2,82 km;

( )b) 3 km;

( )c) 3,6 km;

( )d) 2,75 km;

( )e) 2,91 km.

05. Um morador possui em sua casa um espaço, usado para o cultivo de algumas plantas. O formato desse canteiro é de um setor circular de raio $r =10 m$. Sabendo que o ângulo central desse setor circular é de $\alpha = 60^{0}$, qual é a área do espaço usado para plantio na casa desse jardineiro?

( )a) $52,33\, m^{2}$;

( )b) $10,47\, m^{2}$;

( )c) $31,4\, m^{2}$;

( )d) $20,94\, m^{2}$;

( )e) $100\, m^{2}$.

06. Testes efetuados em um pneu de corrida constataram que, a partir de 185 600 voltas, ele passa a se deteriorar, podendo causar riscos à segurança do piloto. Sabendo que o diâmetro do pneu é de$D= 0,5 m$, ele poderá percorrer, sem riscos para o piloto, aproximadamente:

( )a) 93 km;

( )b) 196 km;

( )c) 366 km;

( )d) 592 km;

( )e) 291 km.

07. O ponteiro dos minutos de um relógio mede$r = 4\, cm$. Supondo $\pi = 3$, a distância, em centímetros, que a extremidade desse ponteiro percorre em 25 minutos é:

( )a) 15;

( )b) 12;

( )c) 20;

( )d) 25;

( )e) 10.

08. Em um motor há duas polias ligadas por uma correia, de acordo com o esquema abaixo.

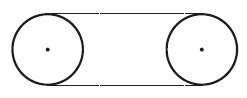
Se cada polia tem raio de 10 cm e a distância entre seus centros é de 30 cm, qual das medidas abaixo mais se aproxima do comprimento da correia?

( )a) 122,8 cm;

( )b) 102,4 cm;

( )c) 92,8 cm;

( )d) 50 cm;

( )e) 32,4 cm.

09. Os raios das rodas traseiras de um trator medem $r=75 cm$ e dão 30 voltas, ao mesmo tempo em que as rodas dianteiras dão 90 voltas. O raio de cada uma das rodas dianteiras mede:

( )a) 20 cm;

( )b) 30 cm;

( )c) 25 cm;

( )d) 18 cm;

( )e) 24 cm.

10. Qual o perímetro de uma circunferência cujo raio mede 3 cm?

Aplicando a fórmula:

$C={2\cdot\pi\cdot r}$

$C={2\cdot{3,14}\cdot 3}

$C=18,84\, cm$

11. (Enem–2010). Uma fábrica de tubos acondiciona tubos cilíndricos menores dentro de outros tubos cilíndricos. A figura mostra uma situação em que quatro tubos cilíndricos estão acondicionados perfeitamente em um tubo com raio maior.

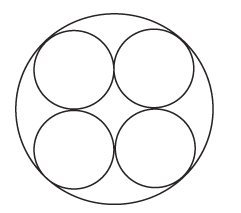
Suponha que você seja o operador da máquina que produzirá os tubos maiores em que serão colocados, sem ajustes ou folgas, quatro tubos cilíndricos internos. Se o raio da base de cada um dos cilindros menores for igual a 6 cm, a máquina por você operada deverá ser ajustada para produzir tubos maiores, com raio da base igual a

( )a) $12\, cm$;

( )b) $12\sqrt{2}\, cm$;

( )c)$24\sqrt{2}\, cm$;

( )d) $6{\left(1 + \sqrt{2}\right)}\, cm$

( )e)$ 12\left({1 +\sqrt{2}}\right)\, cm$

Se ficarem dúvidas, peça ajuda pelos canais abaixo listados. Não guarde suas dificuldades para si. Compartilhe que lhe ajudarei.

Curitiba, 15 de fevereiro de 2020

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

14 de fevereiro de 202023 de novembro de 2020

Matemática – Geometria – Geometria plana.

Polígonos de múltiplos lados.

Em postagens anteriores, abordamos todos os tipos de polígonos, até os de sete lados.

O que notamos é que os polígonos que apresentam cálculos em si mais complexos são os com número ímpar de lados, especialmente os que correspondem aos números primos. Mas podemos notar que há alguns passos que se tornam repetitivos. As dificuldades ficam por conta das aproximações decimais, dos ângulos com medidas não exatas e as razões trigonométricas.

Vejamos o caso do Octógono.

A divisão do círculo em oito partes, resulta em um ângulo central de $\alpha = 45^{0}$. Os lados formarão ângulos internos que suplementam o ângulo central.

$\hat{i}_{8} = 180^{0} – 45^{0} = 135^{0}$

Desse modo: $\hat{S}_{i_{8}}= {8\cdot{135}^{0}} = 1080^{0}$

Da mesma forma podemos calcular o número de diagonais da figura:

$D_{8} ={{\left({n – 3}\right)\cdot n}\over 2}$

$D_{8} ={{\left({8 – 3}\right)\cdot 8}\over 2} = {{5\cdot 8}\over 2} = 20\, diagonais$

O lado dos triângulos, ou seja o raio da circunferência circunscrita, será sempre à distância do centro a qualquer um dos vértices.

O apótema, calcularemos dividindo um dos triângulos centrais em dois triângulos retângulos, como fizemos nos casos anteriores.

Os demais cálculos serão uma repetição da mesma forma.

O eneágono: – polígono de nove lados, nos fornecerá um ângulo central de $\alpha = 40^{0}$

Embora seja um número ímpar de lados, não apresenta ângulos que resultam em divisões aproximadas.

$\hat{i}_{9} = {180}^{0} – 40^{0}= {140}^{0}$.

Soma dos ângulos internos:

$S_{i_{9}}= {{{180}^{0}\cdot 9} – {360}^{0}} = 1260^{0}$

Número de diagonais:

$D_{9} ={{\left({n – 3}\right)\cdot n}\over 2}$

$D_{9} ={{\left({9 – 3}\right)\cdot 9}\over 2} = 27$

E se for um Decágono?

Terá 10(dez) lados. Os ângulos centrais dos triângulos irão medir $\alpha = 36^{0}$

Os ângulos internos medirão:

$\hat{i}_{10} = 180^{0} -36^{0} = 144^{0}$

$S_{i_{10}} = {{{180}^{0}\cdot {10}} – {360}^{0}} = {1440}^{0}$

Número de diagonais:

$D_{10}={{\left({n – 3}\right)\cdot n}\over 2}$

$D_{10}={{\left({10 – 3}\right)\cdot{10}}\over 2}$

$D_{10} ={{7\cdot{10}}\over 2} = 35$

Exercitando

01. Determine o apótema, a área de cada triângulo e a área total de um eneágono regular inscrito em uma circunferência de raio $R = 12,0\, cm$.

Se o polígono inscrito na circunferência é um eneágono, sabemos que ele tem 9(nove) lados e também 9(nove) vértices.

A figura resulta em um total de 9(nove) triângulos isósceles congruentes. O ângulo central de cada um será:

$\hat{c} = {{360^{0}}\over 9} = {40}^{0}$

Cada ângulo interno irá valer:

$\hat{i}_{9}= {180^{0}} – {40}^{0}= {140}^{0}$

O apótema divide cada triângulo em dois triângulos retângulos congruentes.

Ele é calculado a partir da da metade do ângulo interno ${70}^{0}$.

$sen(70^{0}) ={a\over R}$

$a = R\cdot sen(70^{0})$

$a = {12,0}\cdot {0,94}$

$a = 11,28\, cm$

Área de um triângulo

Vamos determinar a medida do lado do eneágono.

$R^2 = a^2 + {l\over2}^2$$\Leftrightarrow$${l^2 \over 4} = {12,0}^2 – {11,28}^2 $

$l^2 = 4\cdot{144,0 – 127,24}$$\Leftrightarrow$$\sqrt{l^2}=\sqrt{4\cdot{16,76}}$

$l = 2\cdot {4,09}$$\Leftrightarrow$$l = 8,18\, cm$

$A_{\Delta_{i}} = {{a\cdot l}\over 2}$$\Leftrightarrow$$A_{\Delta_{i}}= {{11,28}\cdot{8,18}\over 2}$

$A_{\Delta_{i}}=46,14\,cm^2$

No polígono há 9(nove) triângulos desses:

$A_{9} = {{46,14}\cdot 9} = 415,26\, cm^2$

02. Determinar o ângulo central, a medida do lado, do apótema, área de cada triângulo e a área do polígono de 15(quinze) lados inscrito em uma circunferência de raio $R=20,0\, cm$.

Ângulo central:

$\hat{c} = {{360}^{0}}{15} = {24}^{0}$

O ângulo interno:

$\hat{i} = {{180}^{0} – {24}^{0} = {156}^{0}$

Isso indica que o ângulo da base do triângulo será:

$\hat{b} = \frac{{156}^{0}}{ 2} = {78}^{0}$

O apótema será: $sen({78}^{0})= \frac{a}{R}$

$a = R\cdot sen({78}^{0})$$\Leftrightarrow$$a = {20,0}\cdot sen({78}^{0})$

$a = {20,0}\cdot {0,9781} = 19,56\,cm$

O lado do polígono irá medir:

$R^2 = a^2 + {\frac{l}{ 2}}^{2}$$\Leftrightarrow$${\frac{l}{2}}^{2} ={20,0}^{2} – {19,56}^{2}$

$l^2 = 4\cdot{400,0 – 382,7081}$$\Leftrightarrow$$\sqrt{l^2} =\sqrt{4\cdot{17,29}}$

$l = 8,32\, cm$

Área de um triângulo

$A_{Delta_15}={{8,32}\cdot{19,56}\over 2}= 81,37\,cm^2$

O polígono terá ao todo:

$A_{15}= {81,37}\cdot{15}=1220,55\,cm^2$

Vamos treinar por conta?!

01. Um dodecágono está inscrito em uma circunferência, cujo raio mede $R= 16,0\,m$. Determine o apótema, o lado do polígono e as áreas de cada triângulo, bem como do polígono todo.

02. O apótema de um polígono regular de 10 lados mede $a = 25,0\, cm$. Determine a medida do raio da circunferência, o lado do polígono, a área de um triângulo e a area total do polígono.

03. Se um polígono de 18 lados tem o lado medindo $l = 20,0\, cm$. Determine o apótema, o raio da circunferência circunscrita, o ângulo interno, a soma dos ângulos internos, a área do polígono.

04. Uma circunferência tem diâmetro $D=60,0 cm$. Inscrevendo-se nela um polígono de 30(trinta) lados, pede-se: a)a medida do ângulo central; b) a medida dos ângulos internos e a soma dos mesmos; c)o número de diagonais do polígono; d)a medida do apótema e do lado do polígono; e)a área de um triângulo e a área total do polígono.

Havendo dúvidas, peça ajuda por meio de um dos canais que seguem listados abaixo.

Curitiba, 14 de fevereiro de 2020.