Voltemos aos conceitos básicos de geometria ou conceitos primitivos. Aqueles que não têm uma definição, mas servem de base para definir os outros elementos que vem em sua esteira.
Plano

Vimos na geometria plana que um plano é um conjunto infinito de pontos que podemos imaginar ao olhar para uma folha de papel ou o tampo de uma mesa, uma parede e estendendo essa porção de plano até o infinito. Em geral o plano é representado por um quadrilátero, como se fosse uma folha de papel em perspectiva.
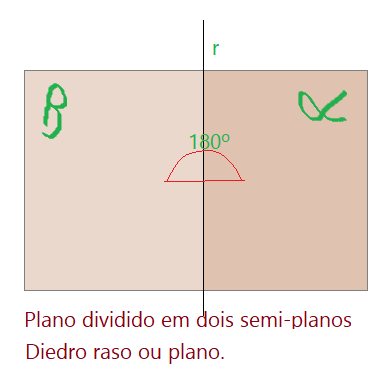
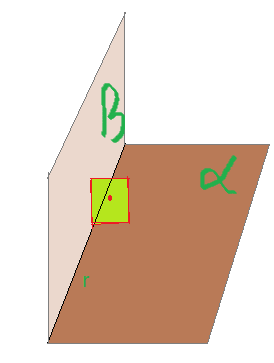
Dividindo um plano por uma reta $r$, obtemos dois semiplanos, como mostra a figura que segue abaixo.
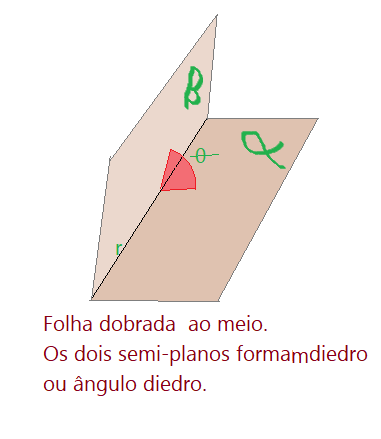
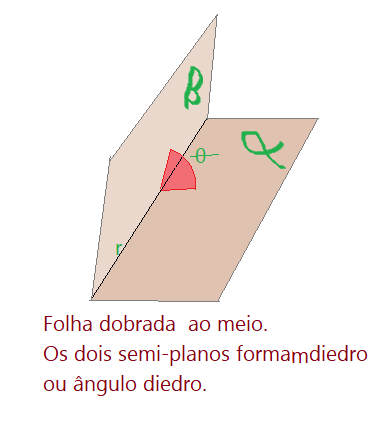
Depois dobramos a folha segundo a reta $r$, obtendo uma figura formada pelos dois semiplanos e uma aresta que é a reta. Esta figura é um diedro.
Os dois semiplanos passaremos a denominar faces do diedro. A reta que é formada pelos pontos de contato das faces denominamos aresta.
Neste diedro temos pois as faces $\alpha \land \beta$, a reta $r$ é a aresta. Entre as faces temos o ângulo $\theta$ que mede a abertura do diedro. É também denominado ângulo diedro.
Classificação dos diedros
a) Diedro nulo: – é o diedro formado por dois semiplanos ou faces sobrepostas.
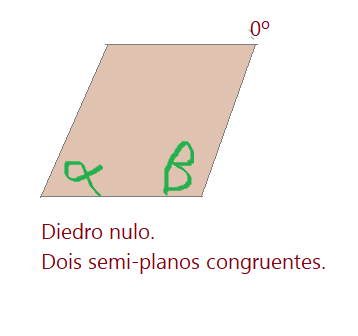
$\theta = 0^0$$\to $ diedro nulo.
b) Diedro raso ou plano: – diedro formado por dois semiplanos opostos, isto é, formados por um plano cortado por uma reta. Podemos visualizar na figura do plano dividido pela reta acima.
$\theta = 180^0$
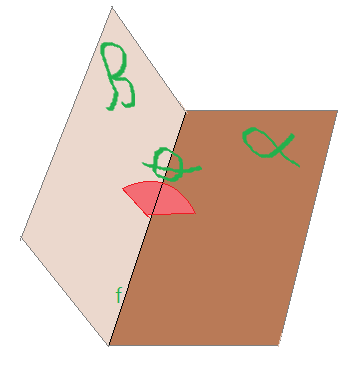
c) Diedro reto: – é o diedro em que as faces formam entre si um ângulo reto.
$\theta = 90^0$
d) Diedro agudo: – o ângulo formado pelas faces do diedro é um ângulo agudo, isto é, menor que $90^0$
$\theta \lt 90^{0}$
e) Diedro obtuso: – o ângulo entre as faces do diedro é maior que $90^0$.
$\theta \gt 90^0$
f) Diedros adjacentes: – são dois diedros que têm uma face comum e a mesma aresta.
g) Diedros complementares: – são diedros cuja soma dos ângulos é igual a $90^{0}$
h) Diedros suplementares: – são diedros cuja soma dos ângulos é igual a $180^{0}$
Diedro cortado por plano secante
Vejamos a figura a seguir, onde aparece um plano $\gamma$ cortando o diedro num ângulo qualquer.
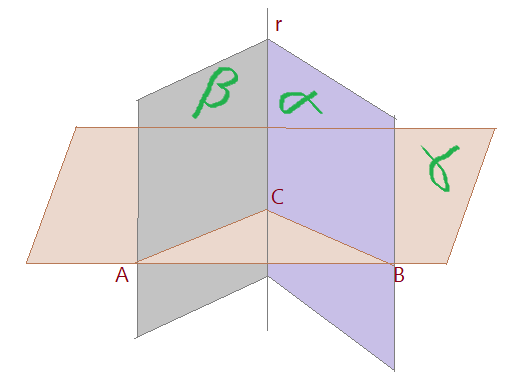
As linhas de intersecção do plano $\gamma$ com as faces do diedro formam o ângulo plano $\widehat{ACB}$.
Intersecção por plano ortogonal.
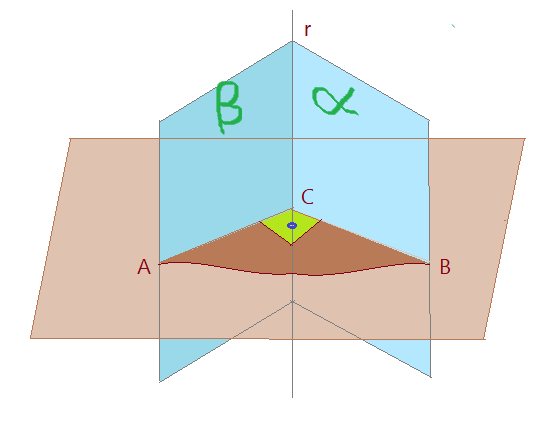
Se o plano secante ao diedro for ortogonal à aresta o ângulo plano $\widehat{ACB}$ formado será igual ao ângulo do diedro, como mostramos na figura a seguir.
Diedros opostos pela aresta.
Imagine dois planos que se interceptam segundo uma linha reta. Mostraremos na figura a seguir como fica, mas certamente, com um pouco de abstração poderá visualizar mentalmente a forma da figura. Cada plano ficará dividido em dois semiplanos, que formarão diedros OPA. Cada semiplano será uma face de dois diedros. Também teremos diedros adjacentes como se pode notar na figura.
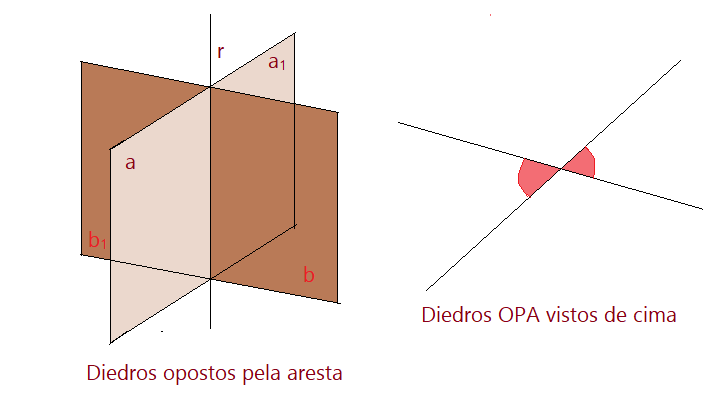
Denominei com as letras $a, a_{1}, b, b_{1}$ os quatro semiplanos. Estes semiplanos são as faces de quatro diedros. Podemos afirmar que os diedros:
$\widehat{arb} \land \widehat{a_{1}rb_{1}}$$\to$ são OPA
$\widehat{arb_{1}} \land \widehat{bra_{1}}$$\to$ são OPA
Os diedros adjacentes tem uma face comum. Assim podemos afirmar que:
$\widehat{arb}\land \widehat{bra_{1}}$$\to$ são adjacentes.
$\widehat{arb}\land\widehat{arb_{1}}$$\to$ são adjacentes.
$\widehat{arb_{1}}\land\widehat{b_{1}ra_{1}}$$\to$ são adjacentes.
$\widehat{bra_{1}}\land\widehat{a_{1}rb_{1}}$$\to$ são adjacentes.
Obs.: Cada um dos diedros da figura é adjacente ao diedro cuja medida é a soma dos outros três diedros determinados e que completa a volta.
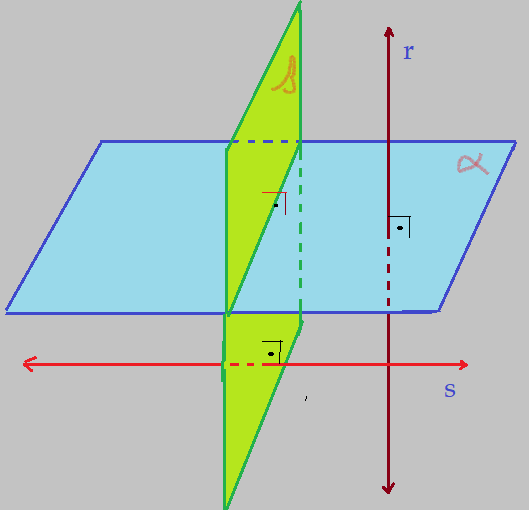
Se a interseção dos planos for ortogonal, teremos quatro diedros retos.
Bissetor de um diedro.
Inserindo em um diedro de medida $\theta = x^0$, de modo a dividí-lo em dois diedros iguais, teremos traçado um bissetor.
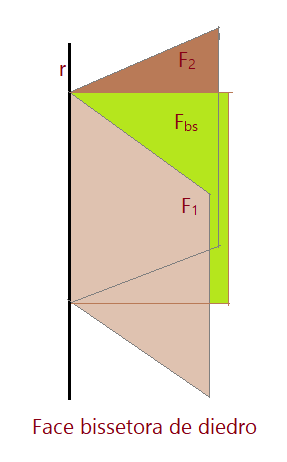
A partir desse ponto denominaremos as faces de um diedro pela letra maiúscula $F$. Para distingui-las entre si usaremos um índice numérico $1,2,3,…$.
Isso posto temos na figura o diedro formado pelas faces $F_{1}\land F_{2}$. A face bissetora é $F_{bs}$. É fácil observar que $F_{bs}$ é comum aos dois diedros resultantes e adjacentes pela aresta.
$\widehat{F_{1}rF_{bs}}\land\widehat{F_{bs}rF_{2}}$$to$ são adjacentes e sua medida é igual à metade de $\widehat{F_{1}rF_{2}}$
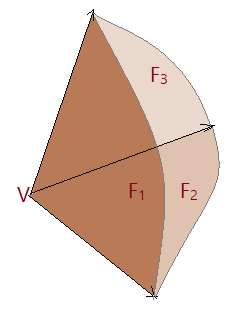
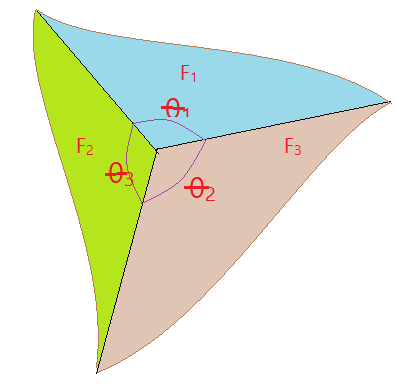
Triedro
A secção de um diedro por um plano secante determina determina um ângulo e as linhas de intersecção serão as arestas de dois novos diedros, o que resulta em uma figura denominada triedro. Vejamos a figura ao lado.

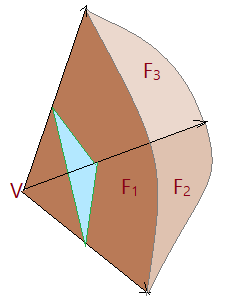
Seccionando um triedro por um plano oblíquo aos lados, as linhas de intersecção formarão um triângulo, que nos é útil para entender os próximos teoremas.

Teorema da relação entre as faces do triedro.
“Em todo triedro a medida de uma face é menor que a soma das medidas das outras duas”.
$F_{1} \lt F_{2} + F_{3}$
$F_{2} \lt F_{1} + F_{3}$
$F_{3} \lt F_{1} + F_{2}$
Obs.: Este teorema pode ser comprovado pela soma dos lados do triângulo de secção.

Teorema do módulo das faces
“Toda face de um triedro é maior que o módulo da diferença entre as outras faces.“
$F_{1}\gt |F_{2} – F_{3}|$
$F_{2}\gt|F_{1} – F_{3}|$
$F_{3}\gt |F_{2} – F_{1}|$
Teorema da soma das medidas das faces
“A soma das medidas das faces expressas em graus é menor que $360^{0}$.
$F_{1} + F_{2} + F_{3} \lt 360^{0}$
Classificação dos triedros
a) Triedro agudo: – as faces do triedro medem menos que $90^0$.
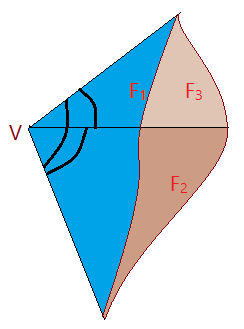
A soma das medidas das faces é menor do que $270^{0}$
b) Triedro reto: – as faces medem todas $90^{0}$.
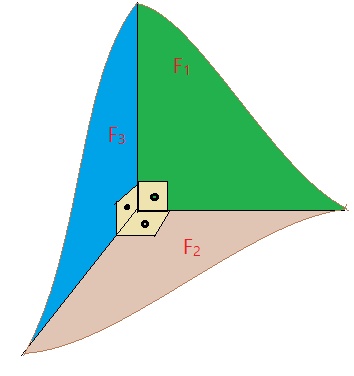
A soma das medidas das faces é igual a $270^{0}$
c) Triedro obtuso: – as faces medem acima de $90^{0}$ e sua soma é menor do que $360^{0}$
d) Triedros adjacentes: – são dois triedros que possuem uma face comum aos dois.
Teorema da soma dos diedros que formam o triedro
Se observarmos um triedro perceberemos que cada duas faces formam um diedro. Denominando-os $D_{1}, D_{2} e D_{3}$, temos que: “ A soma dos diedros formadores do triedro é maior que $180^{0}$ e menor que $540^{0}$”
$180^{0}\lt D_{1} + D_{2} + D_{3} \lt 540^{0}$
Para compreender esse teorema, temos que lembrar que cada diedro tem sua medida compreendida no intervalo entre $0^{0}$ e $180^{0}$. Isso nos leva a entender o limite superior da soma dos três diedros. Se são três, teremos $3\times D \lt 540^{0}$. Um plano secionando o triedro, forma um triângulo, cuja soma dos ângulos internos será sempre igual a $180^{0}$. Dessa forma a soma dos ângulos diedros será sempre maior do que esse valor.
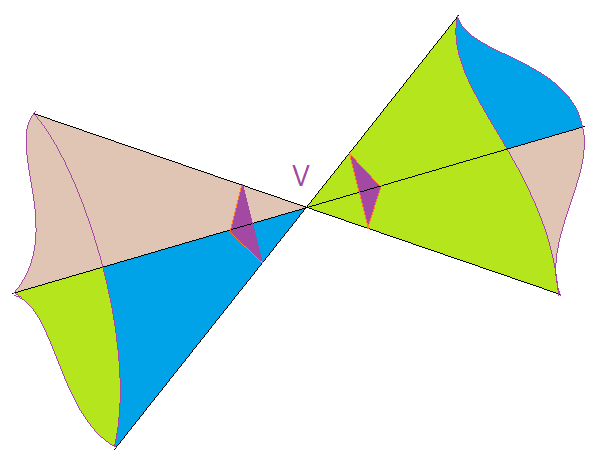
Triedros opostos pelo vértice
São dois triedros cujas arestas são concorrentes no mesmo ponto e estão contidas em semi retas colineares, com origem no ponto de intersecção, que é o vértice.
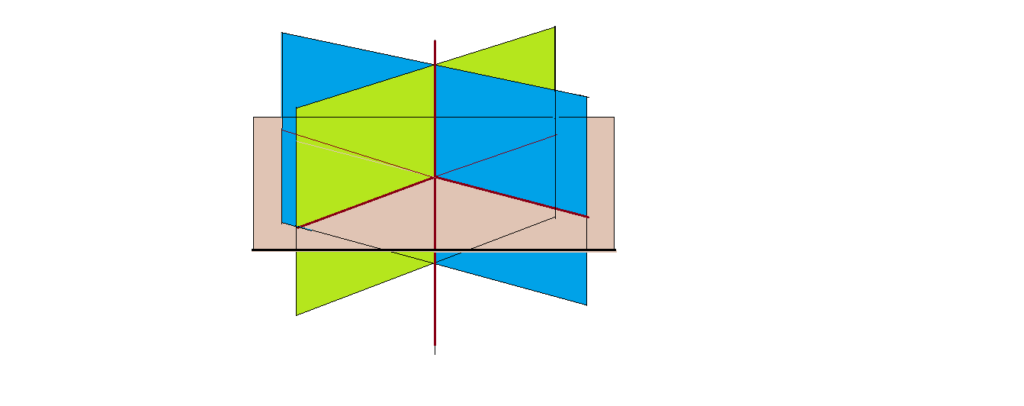
Traçando um par de planos ortogonais, seccionados por um terceiro plano, ortogonal à intercessão dos dois primeiros, formaremos um conjunto de oito triedros retos, opostos pelo vértice dois a dois e adjacentes dois a dois. Veja a figura.
Exercitemos um pouco.
01. Se em um triedro houver dois diedros medindo respectivamente $60^{0}$ e $110^{0}$. Qual é o intervalo em que estará compreendida a medida do terceiro diedro?
Vimos que em qualquer triedro há três faces, cujas medidas seguem a regra:
$180^{0}\lt F_{1} + F_{2} + F_{3}\lt 540^{0}$
$180^{0}\lt 60^{0} + 110^{0} + F_{3}\lt 540^{0}$
$180^{0} – 170^{0}\lt F_{3} \lt 540^{0} – 170^{0}$
$10^{0}\lt F_{3}\lt 370^{0}$
Também vimos que:
$F_{3}\lt F_{1} + F_{2}$$\Leftrightarrow$$F_{3}\lt 60^{0} + 110^{0}$
$F_{3}\lt 170^{0}$
A intercessão dos dois intervalos nos dará o intervalos que responde à nossa questão:
$F_{3} = \{X| 10^{0} \lt X \lt 170^{0}\}$
02. Em um triedro duas faces medem $100^{0}$ e $150^{0}$. Quais são os possíveis valores da terceira face?
$F_{1} + F_{2} + F_{3}\lt 360^{0}$$\Leftrightarrow$$100^{0} +150^{0} + X \lt 360^{0}$
$X\lt 360^{0} – 250^{0}$$\Leftrightarrow$$X\lt 110^{0}$
Temos também:
$F_{3}\gt |F_{2} – F_{1}$$\Leftrightarrow$$ X\gt|150 – 100|$
$X \gt 50^{0}$
Fazendo a intercessão dos dois intervalos teremos
$F_{3} = \{X| 50\lt X \lt 110^{0}\}$
03. Se em um triedro dois diedros são retos, o terceiro diedro necessariamente estará compreendido em qual intervalo?
$180^{0}\lt 90^{0} + 90^{0} + X \lt 540^{0}$
$180^{0} – 180^{0} \lt X \lt 540^{0} – 180^{0}$
$0^{0}\lt X \lt 360^{0}$
$D_{3} = \{X| 0^{0}\lt X \lt360^{0}\}$
04. Responder se está certa ou errada a afirmação e justifique sua resposta.
4.1. O ângulo de um diedro é ângulo de secção reta.
4.2. Se duas secções de um diedro são congruentes, então elas são paralelas.
4.3. Não existe o triedro cujas faces medem $120^{0}, 75^{0} e 45^{0}$
4.4. A terceira face do triedro, cujas duas outras medem $50^{0} e 130^{0}$ devem ser maior que $60^{0}$ e menor que $160^{0}$
4.5. O terceiro diedro do triedro, cujos outros dois medem $70^{0} e 130^{0}$ só pode ser $20^{0}\lt X \lt 120^{0}$
05. Dois diedros retos adjacentes são também:
( )a) coincidentes;
( )b) suplementares;
( )c) complementares;
( )d) implementares;
( )e) replementares.
06. Dois triedros adjacentes:
( )a) têm uma face comum;
( )b) têm as mesmas medidas das faces;
( )c) são opostos pelo vértice;
( )d) são complementares;
( )e) são suplementares.
07. Um plano secante a um diedro determina sobre suas faces um:
( )a) triângulo retângulo;
( )b) quadrado;
( )c) um losango;
( )d) triângulo;
( )e) N.d.a.
08. Dois diedros opostos pela aresta determinam também um par de ângulos:
( )a) complementares;
( )b) replementares;
( )c) OPA e suplementares dos dois outros;
( )d) implementares;
( )e) suplementares entre si.
09. Se as medidas das faces de um triedro são $60^{0}$, o triângulo formado por um plano secante ortogonal a linha de intercessão dos bissetores dos diedros será:
( )a) escaleno;
( )b) equilátero e equiângulo;
( )c) retângulo;
( )d) obtusângulo;
( )e) N.d.a.
10. O triângulo que pode funcionar como quarta face para a figura do triedro, transforma o mesmo em um:
( )a) tetraedro;
( )b) cubo;
( )c) pirâmide quadrangular;
( )d) prisma triangular;
( )e) tronco de pirâmide.
Se houver dúvida, use um dos canais abaixo listados para se comunicar e expor suas dificuldades. Estou sempre à disposição para ajudar.
Curitiba, 26 de novembro de 2020
Décio Adams, IWA
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760 Celular e WhatsApp: (41) 99805-0732