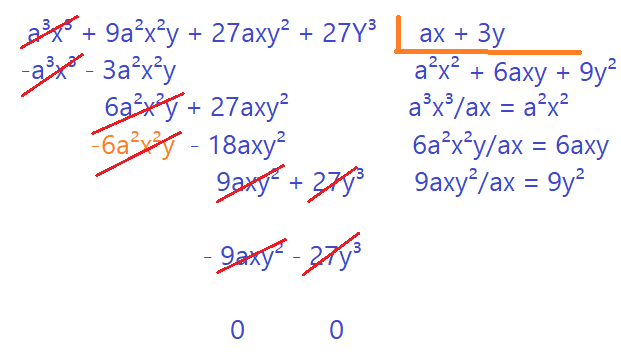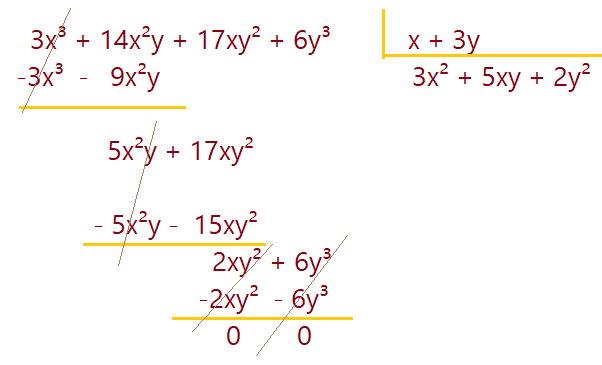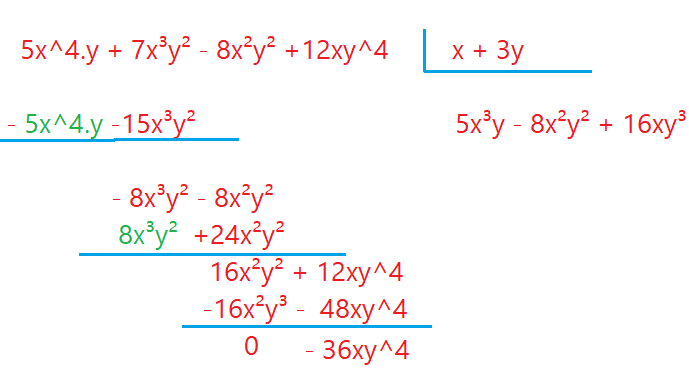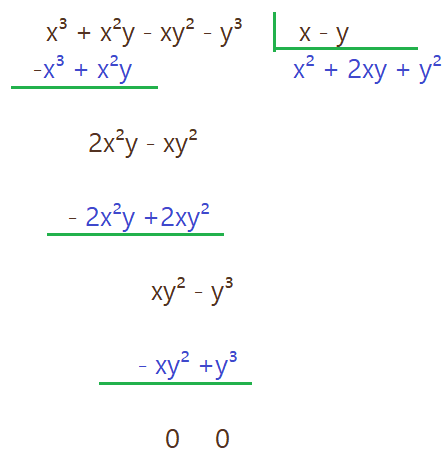junho 2020 – Matemática

29 de junho de 202030 de junho de 2020

01.047-02 – Matemática. Álgebra. – Fatoração de expressões algébricas.

Até aqui fizemos multiplicação, adição, subtração e divisão de polinômios. O que faremos agora é transformar um polinômio numa multiplicação de um termo algébrico por um polinômio, ou um polinômio por outro.

Começaremos pelo caso mais simples. Um polinômio em que todos os termos possuem um fator comum. Colocaremos este fator em “evidência” e multiplicado pelo que resta do polinômio.

Vejamos um exemplo:

\begin{align}\color{Red}{3ax^5 – 6a^2x^3y^2 + 15a^3x^2}\end{align}

Analisando os três termos do polinômio, observamos que todos eles tem em comum:

O fator numérico $3$.
Os fatores literais $ax^2$.

Para obtermos a fatoração do polinômio, iremos multiplicar o mesmo pelos fatores comuns $3ax^2$ e dividir todos os termos pelos mesmos. Vejamos como fica isso;

\begin{align}{3ax^2}\times\frac{3ax^5 – 6a^2x^3y^2 + 15ax^3}{3ax^3}\end{align}

\begin{align}{3ax^2}\times\left({\frac{3ax^5}{3ax^2} – \frac{6a^2x^3y^2}{3ax^2} +\frac{15ax^3}{3ax^2}}\right)\end{align}

\begin{align}\color{NavyBlue}{{3ax^2}\times\left({x^3 – 2axy^2 + 5x}\right)}\end{align}

Vejamos outro exemplo:

\begin{align}{6x^3 + 9x^2y}\end{align}

Fator comum: $3x^2$

Colocando em evidência: \begin{align}{3x^2}\times\left(\frac{6x^3 + 9x^2y}{3x^2}\right)\end{align}

\begin{align}{3x^2}\times\left({\frac{6x^3}{3x^2} + \frac{9x^2y}{3x^2}}\right)\end{align}

\begin{align}\color{NavyBlue}{{3x^2}\left({2x + 3y}\right)}\end{align}

Exercícios de aprendizagem

Fatore as expressões abaixo, colocando em evidência o fator comum a todos os termos.

a)${8m^2 – 10mn^21 + 2m^3}$

b)${7x^3y + 21x^2y^3}$

c)${a^2bx^3 – a^2x^2 + ab^2x}$

d)${6u^5v^3 – 15u^3v^2 – 3u^4v}$

e)${15p^2 + 10p^3r + 5pr^2}$

f)${\frac{10}{3}q^3 – \frac{7}{3}p^2q + 3pq^2}$

g)${16a^2 – 24ab}$

h)${13m^4 – 39m^2n + 26mn^2}$

Fatorando polinômios em produtos notáveis

Vejamos o exemplo.

\begin{align}\color{Sepia}{16 + 8x + x^2}\end{align}

Note que se trata de um trinômio onde há dois termos que são quadrados: $16 $ e $x^2$. O termo do meio é igual ao produto das raízes dos outros dois termos, multiplicado por $2$. Então podemos fatorar esse trinômio em um produto notável que é o quadrado da soma das raízes dos dois termos quadrados.

$\sqrt{16} = 4$ e $\sqrt{x^2} = x$

$$\color{NavyBlue}{{16 + 8x + x^2} = {(4 + x)}^2}$$

Vejamos outro exemplo:

\begin{align}\color{Sepia}{9x^2 – 30xy + 25y^2}\end{align}

Temos o primeiro termo $9x^2$ e o terceiro $25y^2$. O termo do meio é o dobro do produto das raízes quadradas dos outros dois termos, precedido do sinal (-). Logo, a expressão dada pode ser fatorada no quadrado da diferença entre essas raízes. Fica assim:

\begin{align}\color{NavyBlue}{{9x^2 – 30xy + 25y^2} = {(3x – 5y)}^2}\end{align}

Antes de fazer exercícios, vejamos mais um exemplo.

\begin{align}\color{Sepia}{4x^2 – 9}\end{align}

Temos um binômio que representa a diferença entre dois quadrados. Como vimos isso permite que podemos fazer o caminho inverso e escrever na forma de um produto da soma pela diferença.

\begin{align}\color{NavyBlue}{{(2x + 3)}\times{(2x – 3)}}\end{align}

Fatorar em produtos notáveis os trinômios e binômios que seguem.

a)${36 – 36x + 9x^2}$

b)${1 + 10y + 25y^2}$

c)${49z^2 – 64x^2}$

d)${9m^2 – 30m + 25}$

e)${4u^2 + 4\sqrt{5}uv + 5v^2}$

f)${81 – 9v^2}$

g)${3x^2 + 2\sqrt{3}xy + y^2}$

h)${25p^2 + 30pq + 9q^2}$

i}${144 – 24r + r^2}$

j)${121y^2 – 88yz + 16z^2}$

k)${256 – 169w^2}$

Fatoração de polinômios cubos perfeitos.

Vejamos esse exemplo:

\begin{align}\color{Sepia}{27x^3 + 27x^2y + 9xy^2 + y^3}\end{align}

Podemos observar dois termos com expoente $3$. Extraindo a raiz cúbica teremos:

$\sqrt[3]{27x^3} = 3x$ e $\sqrt[3]{y^3} = y$

Lembrando do desenvolvimento do cubo da soma e diferença temos:

$3\times{(3x)}^2\times y = 27x^2y$

$3\times{3x}\times y^2 = 9xy^2$

Resultaram os dois termos intermediários do polinômio e podemos fatorar esse no cubo da soma das raízes dos termos extremos.

\begin{align}\color{NavyBlue}{{27x^3 + 27x^2y + 9xy^2 + y^3} = {(3x + y)}^3}\end{align}

Vejamos mais um exemplo na mesma linha.

\begin{align}\color{Sepia}{8a^3 – 36a^2b + 54ab^2 – 27b^3}\end{align}

Novamente temos dois termos que são cubos perfeitos:

$\sqrt[3]{8a^3} = 2a$ e $\sqrt[3]{27b^3} = 3b$

Lembrando do cubo da diferença:

$-3\times{(2a)}^2\times{(3b)} = -36a^2b$

$ 3\times 2a (3b)^2 = 54ab^2$

Obtivemos os termos intermediários do polinômio e podemos fatorar o mesmo em:

\begin{align}\color{NavyBlue}{{8a^3 – 36a2b + 54ab^2 – 27b^3} = {(2a – 3b)}^3}\end{align}

Um polinômio de quatro termos, sendo dois termos cubos perfeitos.

\begin{align}\color{Sepia}{8x^3 – 4x^2y – 2xy^2 + y^3}\end{align}

$\sqrt[3]{8x^3} = 2x$ e $\sqrt[3]{y^3} = y$

Lembrando do produto da soma de dois números pelo quadrado de sua diferença.

${- 1\times {(2x)}^2\times y = -4x^2y}$

${-1\times {2x}\times y^2 = -2xy^2}$

Estes resultados mostram que o polinômio é o produto da soma de dois termos pelo quadrado de sua diferença.

\begin{align}\color{NavyBlue}{{8x^3 – 4x^2y – 2xy^2 + y^3}={(2x + y)}{(2x – y)}^2}\end{align}

Para completar, vejamos mais um exemplo.

\begin{align}\color{Sepia}{27m^3 + 18m^2n – 12mn^2 – 8n^3}\end{align}

Também aqui podemos tirar a raiz cúbica dos dois termos das extremidades.

$\sqrt[3]{27m^3}=3m$

$\sqrt[3]{ 8n^3} = \pm 2n$

${1\times {(3m)}^2\times 2n = 18m^2n}$

${- 1\times 3m\times {(2n)}^2 = – 12mn^2}$

Lembrando dos produtos notáveis, estamos diante do produto da diferença entre dois termos pelo quadrado de sua soma. O que nos dá o que segue:

\begin{align}\color{NavyBlue}{27m^3 + 18m^2n – 12mn^2 – 8n^3 = {(3m – 2n)}{(3m + 2n)}^2}\end{align}

Mais exercícios sobre esse assunto

Fatore os polinômios em cubos da soma e diferença, bem como produto do quadrado da soma pela diferença e quadrado da diferença pela soma.

a)\begin{align}{27x^3 + 135x^2 + 225x + 125}\end{align}

b)\begin{align}{125-35x – 20x^2 + 8x^3}\end{align}

c)\begin{align}{8y^3 + 12y^2 – 6y – 27}\end{align}

d)\begin{align}{27m^3 + 18m^2n – 12m^2n^2 – 8n^3}\end{align}

e)\begin{align}{a^3 + 3a^2bx + 3ab^2x^2 + b^3x^3}\end{align}

f)\begin{align}{27x^3 + 54x^2y + 36xy^2 + 8y^3}\end{align}

g}\begin{align}{8p^3 – 36p^2q + 54pq^2 – 27q3}\end{align}

h) \begin{align}{343a^3 – 294a^2b + 189ab^2 – 27b^3}\end{align}

i)\begin{align}{27a^3x^3 – 54a^2bx^3 + 36ab^2x^3 – 8b^3x^3}\end{align}

Fatoração de polinômios com fatores comuns

Fatoração por agrupamento

É muito utilizada a fatoração de polinômios que contenham fatores comuns em dois fatores, formando um produto de binômios ou binômio por trinômios. É denominada Fatoração por agrupamento. Fatoramos dois termos e depois os outros dois. Se for possível transformar o polinômio em um produto de binômios, deverão surgir dois fatores comuns entre as partes da primeira etapa. Colocamos em evidência e terminamos o processo.

\begin{align}\color{Brown}{10x + 6 – 15xy – 9y}\end{align}

Temos um fator comum entre os termos $10x + 6$, que é $2$. Também entre os termos $-15xy -9y$, o fator comum é $-3y$. Isso nos permite fatorar os termos dois a dois. Vejamos como fica:

\begin{align}{2\left(\frac{10x + 6}{2}\right) – 3y\left(\frac{-15xy – 9y}{-3y}\right)}\end{align}

\begin{align}{2{\left(\frac{10x}{2} + \frac{6}{2}\right)} – 3y{\left(\frac{-15xy}{-3y} +\frac{-9y}{-3y}\right)}}\end{align}

\begin{align}{2(5x + 3) -3y(5x + 3)}\end{align}

Temos agora dois produtos, onde há um fator comum, que é o binômio $5x + 3$. Podemos colocar esse binômio em evidência e teremos:

\begin{align}\color{NavyBlue}{{(5x + 3)}{(2 – 3y)}}\end{align}

Outro exemplo desse mesmo tipo.

\begin{align}{6axy + 10ax + 9bxy + 15bx}\end{align}

Podemos fatorar os termos aos pares novamente

\begin{align}{2ax\left(\frac{6axy + 10ax}{2ax}\right) + 3bx\left(\frac{9bxy + 15bx}{3bx}\right)}\end{align}

\begin{align}{2ax\left({\frac{6axy}{2ax} +\frac{10ax}{2ax}}\right) + 3bx\left({\frac{9bxy}{3bx} + \frac{15bx}{3bx}}\right)}\end{align}

\begin{align}{2ax(3y + 5) + 3bx(3y + 5)}\end{align}

Temos dois binômios comuns como fatores da expressão agora. Colocamos eles em evidência e ficamos com:

\begin{align}\color{NavyBlue}{{(3y + 5)}{(2ax +3bx)}}\end{align}

Vamos exercitar esse tipo de fatoração.

\begin{align}{10y – 2 +35xy – 7x}\end{align}
\begin{align}{15 – 21y – 20y + 28y^2}\end{align}
\begin{align}{ 14m^2 + 35mn – 6mn -15m^2}\end{align}
\begin{align}{3r + 6 + 15pr + 30p}\end{align}
\begin{align}{20 + 35x – 12x – 21x^2}\end{align}
\begin{align}{50x + 30 – 10x^2 – 6x}\end{align}
\begin{align}{60x +84 + 15xy^2 + 21y^2}\end{align}
\begin{align}{30ax – 6ay + 15bx – 3by}\end{align}
\begin{align}{3ax^2 + 2axy^2 + 3bxy + 2by^3}\end{align}
\begin{align}{16m + 14mn – 24n – 21 nr}\end{align}
\begin{align}{27 + 18v + 15u + 10uv}\end{align}
\begin{align}{55y + 22 – 15xy – 6x}\end{align}
\begin{align}{13a – 78ab + 4b – 24b^2}\end{align}
\begin{align}{15 – 9y – 35x + 21xy}\end{align}
\begin{align}{12w + 8wv + 15v + 10v^2}\end{align}

Se surgir qualquer dúvida, entre em contato comigo para escarecer as dificuldades. Os canais estão listados abaixo.

Curitiba, 29 de junho de 2020

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

28 de junho de 202028 de junho de 2020

01.047-01 – Matemática. Álgebra. Divisão de polinômios por polinômios.

Vamos começar com as divisões exatas, onde não sobram restos. Seja dividir as expressões abaixo.

\begin{align}{(a^3x^3 + 9a^2x^2y + 27axy^2 + 27y^3)}\div {(ax + 3y)}\end{align}

Vamos colocar os polinômios numa chave como fazemos na divisão de números com vários algarismos. Antes vamos verificar se os polinômios estão ordenados segundo os expoentes de uma ou mais variáveis.

Observe que começamos dividindo o primeiro termo do dividendo pelo primeiro do divisor. Multiplicamos todos os termos do divisor e subtraímos os resultados dos termos semelhantes do dividendo. Fica evidente que no primeiro termo o resto deve ser zero. Na sequência colocamos o outro termo do dividendo ao lado do resto e seguimos o procedimento, até que tenhamos utilizado todos os termos do dividendo. Se o resto for zero, a divisão é exata. Se houver resto, no momento de efetuar a multiplicação do quociente pelo divisor, será necessário adicionar esse resto. No exemplo mostrado, a divisão foi exata.

Podemos então escrever o resultado desse modo:

\begin{align}{(a^3x^3 + 9a^2x^2y + 27axy^2 + 27y^3)}\div{(ax + 3y)}\\= {(a^2x^3 + 6axy + 9y^2)}\end{align}

Vejamos mais um exemplo.

\begin{align}{(3x^3 + 14x^2y + 17xy^2 + 6y^3)}\div{(x + 3y)}\end{align}

Mais um exemplo de divisão exata entre dois polinômios. Um detalhe a ser sempre levado em consideração é o grau dos polinômios. O divisor nunca poderá ter grau mais elevado do que o dividendo. Isso nos levaria a uma situação impossível de realizar no campo de álgebra.

\begin{align}{(3x^3 +14x^2y + 17xy^2 + 6y^3)}\div{(x + 3y)} \\= {(3x^2 + 5xy + 2y^2)}\end{align}

Vamos ver um exemplo em que a divisão não seja exata.

\begin{align}{(5x^4y + 7x^3y^2 – 8x^2y^3 + 12xy^4)}\div{(x + 3y)}\end{align}

Para fazer o caminho de retorno, teremos que multiplicar o quociente, pelo divisor e adicionar o resto que ficou ao final do processo. Veja como fica:

\begin{align}{(5x^3y – 8x^2y^2 + 16xy^2)}\times{(x + 3y)} + {-36xy^4}\end{align}

Mais um exemplo para confirmar e tirar as dúvidas.

\begin{align}{(x^2 + x^2y – xy^2 – y^3)}\div{(x – y)}\end{align}

Podemos notar que o quociente e o divisor são fatores que formam um produto notável, que é conhecido como quadrado da soma multiplicado pela diferença. Ele nos ajuda a entender qualquer outra divisão de polinômios entre si.

Chegou a hora de deixar um trabalho para você fazer.

\begin{align}{(x^3 +x^2y – sy^2 – y^3)}\div{(x – y)}\\ = {(x^2 + 2xy + y^2)}\end{align}

Efetue a divisão dos polinômios listados a seguir.

a) \begin{align}{(x^3 – x^2y + xy^2 – y^3)}\div {(x + y)}\end{align}

b)\begin{align}{(8a^3x^3 + 4a^2x^2y – 2axy^2 – y^3)}\div{(4a^2x^2 + 4axy + y^2)}\end{align}

c)\begin{align}{(8a^3x^3 – 4a^2x^2y + 2axy^2 – y^3)}\div{(2ax + y)}\end{align}

d)\begin{align}{(81x^4 – 108x^3y + 48xy^3 – 16y^4)}\div{(9x^2 – 4y^2)}\end{align}

e)\begin{align}{(2a^3 – 11a^2b + 12ab^2 + 9b^3)}\div{(2a + b)}\end{align}

f)\begin{align}{(75x^3 – 160x^2z – 68x^2 – 16z^3)}\div{(5x – 2z)}\end{align}

g)\begin{align}{(3u^3v^3 + 5u^2v^2w + uvw^2 -w^3)}\div{(3uv – w)}\end{align}

h)\begin{align}{(10x^3 + 15x^2y -6xy^2 – 2y^3)}\div{(2x – y)}\end{align}

i)\begin{align}{(8a^3x^3 – 4a^2x^2y 6axy^2 – 3y^3)}\div{(2ax + y)}\end{align}

j)\begin{align}{(2a^3 – 11a^2b + 12ab^2 + 13b^3)}\div{(2a + b)}\end{align}

Havendo dúvidas na resolução, faça contato por meio de um dos canais que estão listados abaixo. Estou disponível para ajudar.

Curitiba, 28 de junho de 2020

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

15 de junho de 202021 de junho de 2020

01.035 – Matemática – Aritmética. Razão e proporção. Regra de três composta.

No estudo da regra de três simples, usamos apenas duas grandezas que se relacionam. Sendo um dos valores desconhecido, é possível descobrir seu valor com o uso dos outros três valores conhecidos, formando uma proporção. A aplicação das regras das proporções nos fornece procedimentos para atingir nossa finalidade.

Quando o problema envolve três ou mais grandezas, a regra simples não nos ajuda. Mas podemos recorrer à chamada Regra de Três composta. Para isso é conveniente elaborar uma tabela com tantas colunas quantas forem as grandezas. Haverá grandezas diretamente proporcionais e as inversamente proporcionais, ocasionando a inversão da ordem em que aparecem no cálculo. Vamos tomar um exemplo.

Sabendo que $5$ torneiras iguais, totalmente abertas, enchem um tanque de $6000$ litros de água, em $4$ horas de fluxo. Se colocarmos $8$ torneiras iguais, enchendo um tanque de $10000$ litros, qual será o tempo para conclusão do processo?

Torneiras	Litros	Horas
5	6000	4
8	10000	X

Analisando o problema, notamos que, se o volume de água permanecer o mesmo, o número maior de torneiras tornará o tempo gasto menor. O que nos leva a concluir que o número de torneiras é inversamente proporcional ao tempo.
Se o número de torneiras permanecer constante, haverá uma demora maior do que as 4 horas para encher o tanque de 10000 litros. Volume de água e tempo diretamente proporcionais. Então podemos escrever a proporção da seguinte forma.

$ {4\over X} ={8\over 5}\times{6000\over 10000}$

${4\over X} = {48000\over 50000}$

Multiplicando os extremos e os meios entre si, teremos:

$48000\times X = 4\times 50000$$\Leftrightarrow$$X = {200000\over 48000}$

$$\color{Brown}{X \simeq 4,17 horas}$$

2. Usando um ferro elétrico $1$ hora por dia, durante $20$ dias, o consumo de energia será de $10\, kW/h$. Se o mesmo ferro elétrico for usado $110$ minutos por dia durante $30$ dias, qual será o consumo?

tempo/dia	Dias	Consumo(kW/h)
60	20	10
110	30	x

As grandezas todas são diretamente proporcionais. Usando o ferro por mais dias, aumentará o consumo. Usando o mesmo ferro por mais tempo diariamente o consumo em 20 dias também aumentará. Então a proporção ficará:

${10\over X} = {60\over 110}\times{20\over 30}$$\Leftrightarrow$${10\over X} = {1200\over 3300 }$

$ 1200\times X = 10\times 3300$$\Leftrightarrow$$ X = {10\times 3300\over 1200}$

$$\color{Sepia}{X = 27,5\, kW/h}$$

3. Trabalhando $10$ horas por dia, durante $18$ dias, João recebeu $R\$ 2 100,00$. Se trabalhar $8$ horas por dia, quantos dias ele deverá trabalhar para receber $R\$ 2 700,00$?

Horas/dia	Dias	Remuneração
10	18	2.100,00
8	x	2.700,00

O número de horas diárias é inversamente proporcional ao número de dias. Os dias de trabalho são proporcionais ao valor da remuneração. Então devemos estabelecer a proporção:

${18\over X} = {8\over 10}\times{2100,00\over 2700,00}$$\Leftrightarrow$${18\over X}= {16800,00\over 27000,0}$

${16800\times X} = {27000\times 18}$$\Leftrightarrow$$X ={27000\times 18\over 16800}$

$$\color{Sepia}{x\simeq 29 dias}$$

4. Em uma empresa, $10$ funcionários produzem $3 000$ peças, trabalhando $8$ horas por dia durante $5$ dias. O número de funcionários necessários para que essa empresa produza $7 000$ peças em $15$ dias, trabalhando $4$ horas por dia, será de quanto?

Nº funcionários	Nº peças	h/dia	Dias
10	3000	8	5
X	7000	4	15

O número de peças é proporcional ao número de funcionários. O número de horas dia é inversamente proporcional ao número de funcionários. O número de dias é inversamente proporcional ao número de funcionários. Portanto a proporção fica sendo:

${10\over X} = {3000\over 7000}\times{4\over 8}\times{15\over 5}$

${10\over X} = {3000\times\not{4}\times\not{15}\over 7000\times\not{8}\times\not{5}}$

${10\over X} ={30\times 3\over 70\times 2}$$\Leftrightarrow$${90\times X} = {10\times 140}$

$$\color{Sepia}{X ={1400\over 90}\simeq15,56}$$

Serão 16 funcionários pois não existe fração de funcionário.

Exercitando.

01. (Unifor–CE) Se $6$ impressoras iguais produzem $1000$ panfletos em $40$ minutos, em quanto tempo $3$ dessas impressoras produziriam $2000$ desses panfletos?

02.(UFMG)- Uma empresa tem $750$ empregados e comprou marmitas individuais congeladas suficientes para o almoço deles durante $25$ dias. Se essa empresa tivesse mais $500$ empregados, a quantidade de marmitas adquiridas seria suficiente para quantos dias?

03.(Unifor–CE)Um texto ocupa $6$ páginas de $45$ linhas cada uma, com $80$ letras (ou espaços) em cada linha. Para torná-lo mais legível, diminui-se para $30$ o número de linhas por página e para $40$ o número de letras (ou espaços) por linha. Considerando as novas condições, determine o número de páginas ocupadas.

04.(UFRGS-RS)-Se foram empregados $4\, kg$ de fios para tecer $14$ m de uma maquete de fazenda com $80\,cm$ de largura, quantos quilogramas serão necessários para produzir $350\,m$ de uma maquete de fazenda com $120\,cm$ largura?

05.Em $8 horas$, $20$ caminhões descarregam $160\,m^{3}$ de areia. Em $5 horas$, quantos caminhões serão necessários para descarregar $125\,m^{3}$?

06.Em uma fábrica de brinquedos, $8$ homens montam $20$ carrinhos em $5$ dias. Quantos carrinhos serão montados por $4$ homens em $16$ dias?

07.Dois pedreiros levam $9$ dias para construir um muro com $2\,m$ de altura. Trabalhando $3$ pedreiros e aumentando a altura para $4\,m$, qual será o tempo necessário para completar esse muro?

08. Três torneiras enchem uma piscina em $10$ horas. Quantas horas levarão $10$ torneiras para encher $2$ piscinas?

09.Uma equipe composta de $15$ homens extrai, em $30$ dias, $3,6$ toneladas de carvão. Se a equipe for aumentada para $20$ homens, em quantos dias conseguirão extrair $5,6$ toneladas de carvão?

10.Vinte operários, trabalhando $8$ horas por dia, gastam $18$ dias para construir um muro de $300\,m$. Quanto tempo levará uma turma de $16$ operários, trabalhando $9$ horas por dia, para construir um muro de $225\,m$?

11.Um caminhoneiro entrega uma carga em um mês, viajando $8\, horas$ por dia, a uma velocidade média de $50\,km/h$. Quantas horas por dia ele deveria viajar para entregar essa carga em $20$ dias, a uma velocidade média de $60\,km/h$?

12.Com uma certa quantidade de fio, uma fábrica produz $5400\,m$ de tecido com $90\,cm$ de largura em $50\, minutos$. Quantos metros de tecido, com $1$ metro e $20$ centímetros de largura, seriam produzidos em $25\, minutos$?

Havendo dúvidas na resolução dos exemplos ou sobre o raciocínio a ser desenvolvido de modo geral, use um dos canais abaixo listados para pedir ajuda. Não fique na dúvida. Aproveite para esclarecer tudo sem problema algum.

Curitiba, 15 de junho de 2020

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732