Geometria – Página: 2

Introdução.

O desenvolvimento dos conceitos geométricos foram ocorrendo ao longo da história, especialmente para suprir as necessidades construtivas, demarcações de áreas e outras atividades humanas em sua evolução.

Há evidências do uso de algumas formas geométricas desde a mais remota antiguidade, grandemente nas inscrições denominadas rupestres, nas grutas e cavernas. Eram lugares primitivamente usados para abrigar os seres humanos das intempéries e outros riscos que enfrentavam.

De época mais recente, uma boa parcela de formas geométricas e mesmo alguns cálculos rudimentares, surgiram entre os egípcios para construção de seus sistemas de irrigação agrícola, bem como a demarcação periódica dos lotes destinados ao plantio, após as enchentes benfazejas do Rio Nilo. Foi um filósofo/matemático grego, de nome Euclides, que colocou ordem no caos que era a geometria egípcia. Daí a denominação de Geometria Euclidiana, dada à parte da Geometria que estuda as figuras planas em geral. Ao longo dos séculos foram surgindo novas contribuições de várias origens, até chegarmos aos dias atuais. A Geometria é de grande valia na vida humana, especialmente no desenvolvimento de máquinas e equipamentos, edificações diversas, onde as formas derivam desses conhecimentos.

Conceitos primitivos ou que não se podem definir.

Há alguns conceitos primitivos que podemos apenas descrever, mas não definir ou materializar. Todos os demais conceitos derivam deles, uma vez que os usamos para definir os outros, mais complexos, mais elaborados.

Ponto – Se pegarmos um lápis, muito bem afinado e com ele tocarmos uma folha de papel ou outra superfície, a marca deixada nos dará a ideia de um ponto. Dizemos que nos dá a ideia de ponto, uma vez que este é infinitamente menor, o que equivale a dizer que o ponto não tem dimensão. Os pontos são identificados por meio de letras maiúsculas como A, B, C, D, ou P, Q, R, S e outras.

As marcas feitas na imagem acima, podem servir de uma localização de pontos, mas na realidade não são pontos, são conjuntos de pontos. São pequenas manchas.

Reta – se colocarmos justapostos um número infinito de pontos, sempre na mesma direção, teremos a representação de uma reta. Ela é infinita em ambos os sentidos. Sendo formada por pontos, ela não tem espessura. Um risco com o lápis ou caneta, nos dá uma representação da reta, mas apenas isso. Geralmente usamos uma letra minúscula para identificar uma reta. É comum usar para isso as letras como r, s, t, p, q ou qualquer uma das outras, dependendo das circunstâncias.

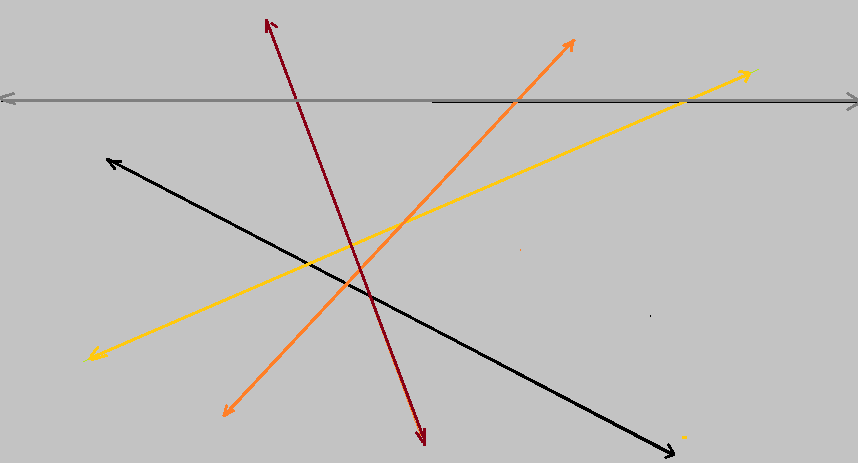
Por um ponto passam infinitas retas. Por dois pontos em um plano, é possível traçar uma e somente uma reta.

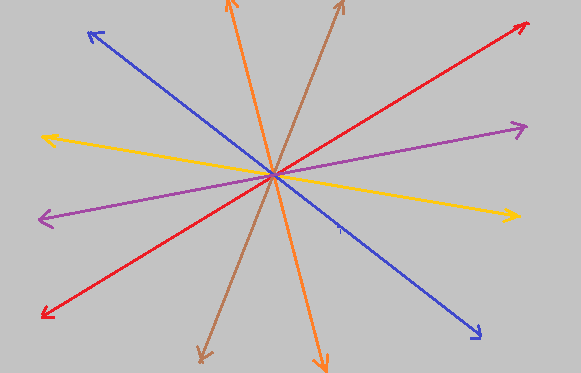
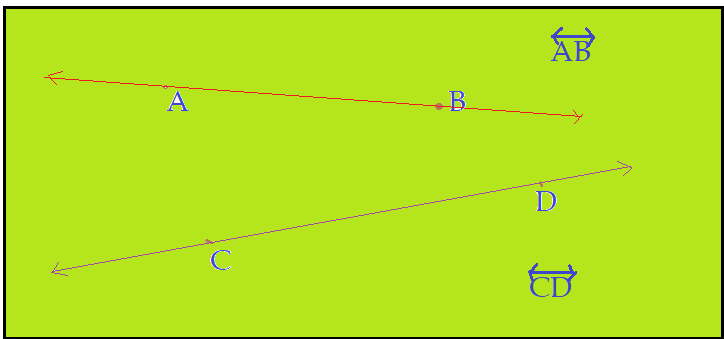
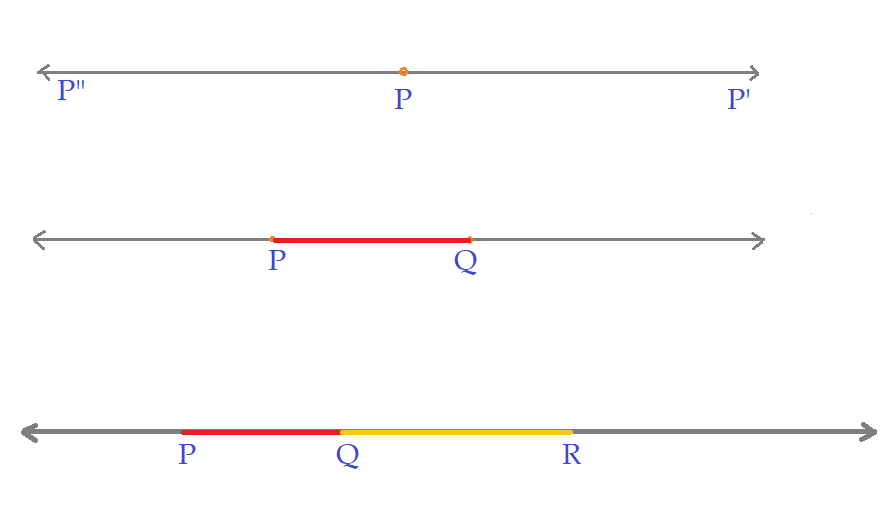
As infinitas retas que podemos traçar pelo ponto, abrangem todo espaço tridimensional.

Pelos pontos ${A}$ e ${B}$, podemos traçar somente a reta ${\overleftrightarrow{AB}}$, assim como pelos pontos ${C}$ e ${D}$, é possível traçar somente a reta ${\overleftrightarrow{CD}}$

Semi-retas: – um ponto sobre uma reta, divide a mesma em duas semi-retas, que têm como origem esse ponto e se prolongam até o infinito na mesma direções e em sentidos opostos. Uma semi-reta é representada pelo ponto de origem e outro ponto identificado, encimados por uma seta partindo da letra origem para a outra letra. Por exemplo ${\overrightarrow{PP’}}$ ou ${\overrightarrow{PP”}}$

Segmentos de reta: – denominamos segmento de reta a parte de uma reta compreendida entre dois pontos identificados sobre ela. Os segmentos de reta são identificados pelas letras associadas as extremidades, encimadas por um traço horizontal. Exemplo ${\overline{PQ}}$

Segmentos consecutivos: – segmentos consecutivos têm uma extremidade comum e fazem parte da mesma reta. Por fazerem parte da mesma reta também são denominados segmentos colineares. Na figura os segmentos ${\overline{PQ} ;\overline{QR}}$

Na primeira reta temos as semi-retas ${\overrightarrow{PP’} e \overrightarrow{PP”}}$. Na segunda reta podemos identificar o segmento de reta ${\overline{PQ}}$ e na terceira reta temos os segmentos consecutivos ${\overline{PQ} e \overline{QR}}$.

Plano: – se olharmos para uma folha de papel sobre uma mesa ou colocada na vertical, podemos imaginar o que é um plano se imaginarmos essa folha se estendendo infinitamente em todas as direções e sentidos imagináveis. O plano é infinito, mas não tem espessura. Um plano geralmente é identificado por uma letra grega, como ${\alpha}$; ${\beta}$; ${\gamma}$.

O plano se estende infinitamente em todas as direções imagináveis prolongando a folha ou a tela do computador.

Classificação de retas

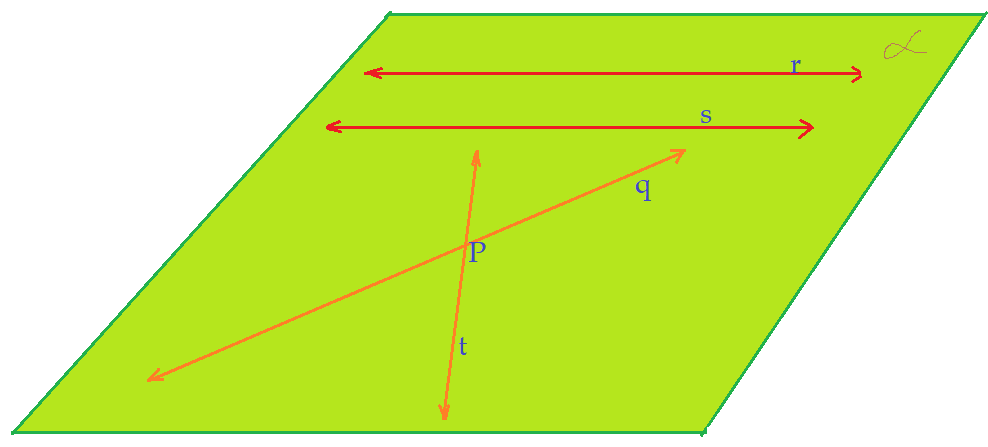
Retas coplanares: – são retas que estão contidas no mesmo plano. Vejamos a figura a seguir.

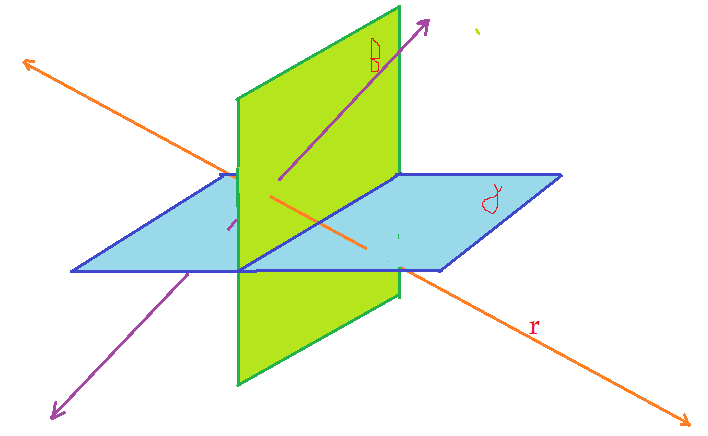
As retas coplanares podem ser paralelas, convergentes ou ortogonais.

Retas de topo: – são retas que perfuram um ou mais planos em qualquer direção, como mostra a figura.

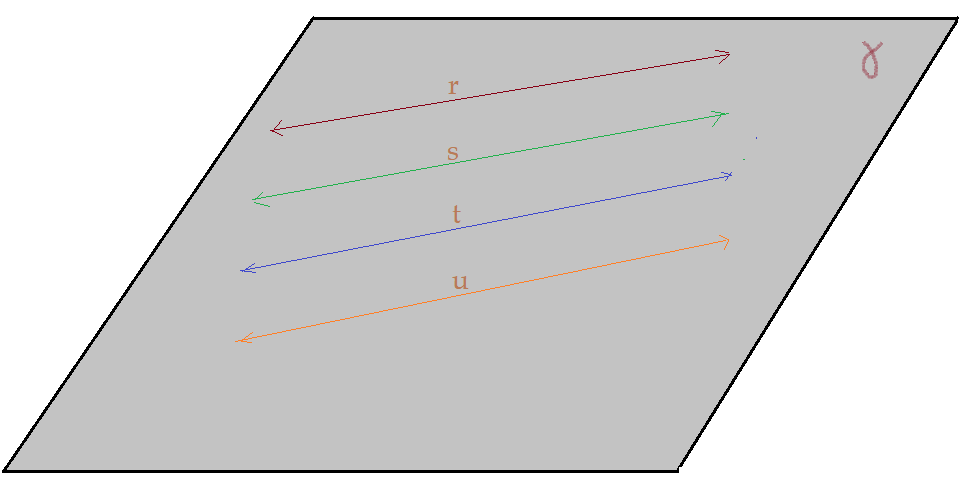
Dois planos ortogonais, são perfurados por retas em diferentes pontos e estas retas são denominadas **retas de topo.**

Retas paralelas: – são retas pertencentes a um mesmo plano e todos os seus pontos sucessivos são equidistantes. Em outras palavras elas se prolongam até o infinito, sem jamais se encontrarem, isto é, não têm nenhum ponto comum.

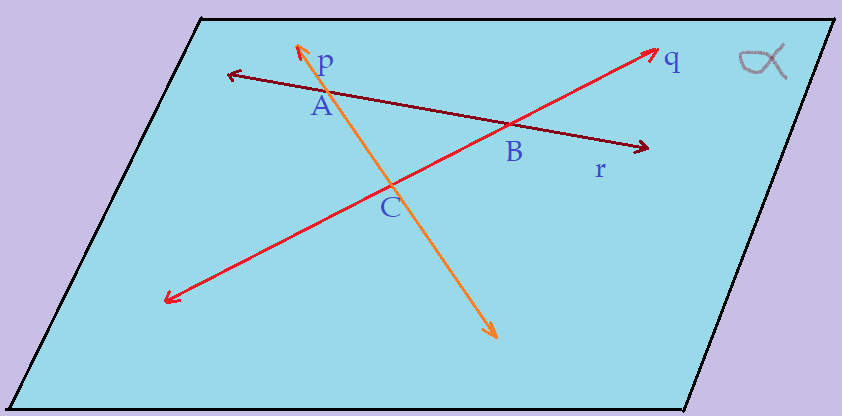
As retas r, s, t, u tem todos seus pontos pertencentes ao plano ${\alpha}$ e no entanto não têm nenhum ponto em comum entre elas.

Retas concorrentes: – são retas que podem pertencer a um mesmo plano e têm um ponto comum. Por um mesmo ponto podemos traçar infinitas retas.

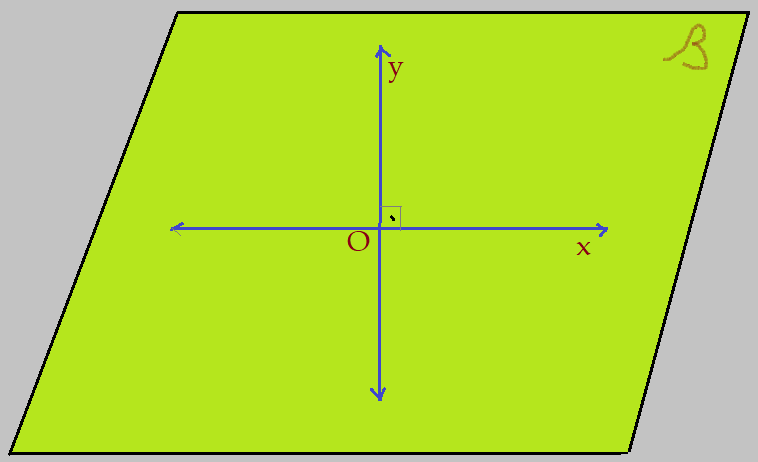
As retas p, q e r pertencem ao mesmo plano ${\alpha}$. As retas p e q, concorrem no ponto C. As retas q e r concorrem no ponto B e as retas p e r convergem ou concorrem no ponto A. Cada uma dessas retas é concorrente de inúmeras retas que passam no mesmo ponto e em pontos diferentes.

Retas ortogonais: – são retas que formam entre elas um ângulo de 90º ou seja um ângulo reto. Elas determinam um plano, como é o caso $\beta$.

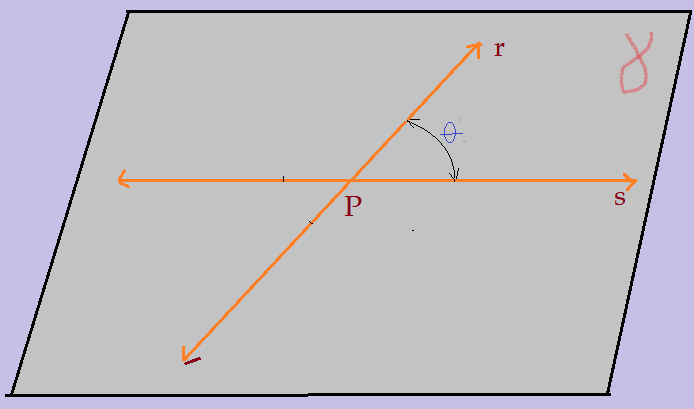
As retas x e y são concorrentes no ponto O e formam um ângulo reto, isto é, os quatro ângulos formados pelas semi-retas são todos iguais a **90º.**

Retas oblíquas: – são retas coplanares que formam ângulos diferentes de 90º. Dois são iguais e menores que 90º e outros dois são iguais e maiores que 90º.

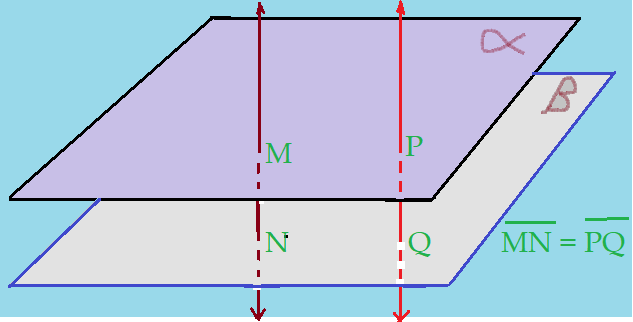
As retas r e s são concorrentes no ponto P e formam dois ângulos ${\theta \lt {90º}}$ e dois ângulos ${\alpha\gt{90º}}$.

Planos paralelos: – são planos cujos pontos determinados por retas ortogonais a eles e paralelas entre si, são sempre equidistantes. Veja ilustração da figura.

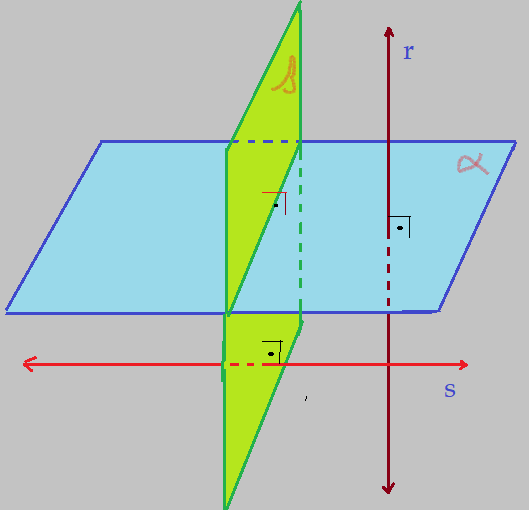
Duas retas paralelas perfuram os planos ${\alpha}$ e ${\beta}$, determinando dois segmentos congruentes (mesma medida) que são ${\overline{MN}}|$ e ${\overline{PQ}}$. Isso demonstra que os planos ${\alpha}$ e ${\beta}$ são paralelos.

Planos ortogonais: – são planos que se interceptam segundo uma linha reta e qualquer reta ortogonal a um deles, será obrigatoriamente paralela ao outro plano.

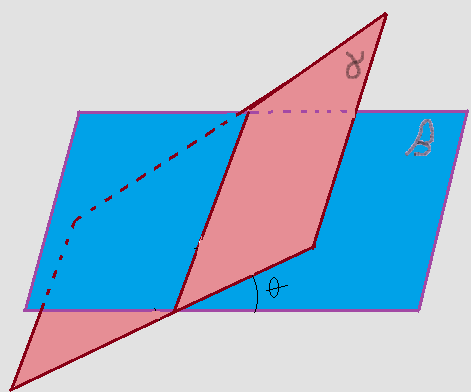
As retas r e s perfuram os planos $\alpha$ e $\beta$ num ângulo que mede $90º$ e são paralelas respectivamente aos dois planos ortogonais. Fica fácil observar que as mesmas retas são também ortogonais entre si.

Planos oblíquos: – são planos que se interceptam segundo uma linha reta, mas formam entre si ângulos $\neq{90º} $. Dois ângulos $\lt{90º}$ e dois angulos $\gt{90º}$.

Os planos oblíquos $\gamma$ e $\beta$ formam dois ângulos $\theta\lt{90º}$ e dois ângulos ${{180º – \theta}\gt{90º}}$.

Já vimos que existem linhas retas, que é o caso mais simples de linha. Agora vejamos os outros tipos de linhas possíveis.

Linhas curvas: – são formadas por um conjunto infinito de pontos, que não estão arrumados na mesma direção. A direção varia em cada ponto da linha.