Vamos “malhar”?
- Determine o conjunto verdade das inequações a seguir.
- $\bbox[5px,border:2px solid brown]{\color{blue}{ 4x – 7 \lt 2x + 1}} $
Observamos que há termos com a variável $x$ tanto no primeiro como no segundo membro da inequação. Igualmente termos independentes da variável. Para obtermos a solução precisamos deixar a variável no primeiro membro e os termos independentes no segundo. Isso fazemos adicionando os simétricos em ambos os lados. Assim:
\[{4x – 7} \lt {2x + 1} \]
\[ \underbrace{\color{blue}{( 4x – 2x)}} +\underbrace{\color{maroon}{ (- 7 + 7) }} \lt \underbrace{\color{blue}{ (2x – 2x)}} + \underbrace{\color{maroon}{( + 1 + 7) }} \]
\[2x + 0 \lt 0 + 8 \] \[{ 2x } \lt { + 8} \]
Para concluir, vamos dividir ambos os membros pelo fator $2$, o que nos deixará a variável $x$ isolada no primeiro membro da inequação. Não há necessidade de mudança de sentido, pois ambos os termos são positivos.
\[ \frac{2x}{2} \lt \frac{+8}{2} \]
\[ x \lt 4 \]
Portanto
\[\bbox[5px,border:2px solid brown]{\color{navy} {V} = \color{navy}{\{ x\in R | x \lt +4 \}}}\]

- $\bbox[5px,border:2px solid brown]{\color{blue}{ 11 + 3x \gt – 8}} $
Vamos isolar $x$ no primeiro membro, adicionando $ – 11$ aos dois membros da inequação.
\[\overbrace{\color{maroon}{ (11 – 11)}} + 3x \gt \overbrace{\color{maroon}{ (-8 -11)}} \] \[ 0 + 3x \gt – 19 \] \[ {3x} \gt {- 19} \]
Dividindo ambos os membros por $3$, iremos isolar $x$ no primeiro membro.
\[ \frac{ (3x) }{ 3 } \gt \frac { (-19) }{ 3 } \] \[x \gt {(-19/3)} \]
\[\bbox[4px,border:2px solid brown]{\color{navy} { V = \left\{ x \in R | x \gt \left(-\frac {19}{3}\right)\right \}}} \]

- $ \bbox[4px,border:2px solid brown]{\color{navy}{- 6 + 2x \ge 3x + 1}}$
Temos que adicionar $\color{brown}{+6}$ e $\color{brown}{-3x}$ a ambos os membros da inequação, para isolar a variável $\color{brown}{x}$ no primeiro membro.
\[ \underbrace{\color{maroon}{ (- 6 + 6)}} +\underbrace{\color{blue}{(2x – 3x)}} \ge \underbrace{\color{blue}{(3x – 3x)}} + \underbrace{\color{maroon}{(1 +6)}}\]
\[ 0 – x \ge 0 + 7 \] \[ {-x} \ge 7 \]
Multiplicamos por $\color{brown}{ -1}$ para deixar $\color{brown}{x}$ com sinal positivo, invertendo dessa maneira a desigualdade.
\[{-x}\cdot {(-1)} \ge {+7}\cdot {(-1)}\] \[ x \le (-7) \]
\[\bbox[4px,border:2px solid brown]{\color{navy}{V = \{ x \in R | x \le (-7) \}}}\]

- $\bbox[5px,border:2px solid brown]{\color{navy}{ 6 \le 5 – 3x}} $
Para trazermos a variável para o primeiro membro, adicionamos seu simétrico $\color{brown}{3x}$, bem como o simétrico $\color{brown}{-6}$ do termo independente. Obtemos assim:
\[ \underbrace{\color{maroon}{(6 – 6)}} + 3x \le \underbrace{\color{maroon}{ (5 – 6)}} + \underbrace{\color{blue}{(-3x + 3x)}} \]
\[ 0 + 3x \le -1 + 0 \] \[ 3x \le -1 \]
Dividindo por $\color{brown}{3}$ ambos os membros, temos:
\[ \frac{3x}{3} \le \frac{(-1)}{3} \]
\[ x \le \left(-{\frac{1}{3}}\right) \]
\[\bbox[5px,border:2px solid brown]{\color{navy}{ V = \left\{ x \in R | x \le \left({-\frac{1}{3}}\right) \right\}}} \]

- $\bbox[5px,border:2px solid brown]{\color{navy}{ 3y + 4 \le 7 – y}} $
Adicionando a ambos os membros da inequação os simétricos $\color{brown}{ -4}$ e $\color{brown}{+y}$, teremos:
\[ \underbrace{\color{blue}{(3y + y) }} + \underbrace{\color{maroon}{(4 – 4)}} \le \underbrace{\color{maroon}{(7 – 4)}} + \underbrace{\color{blue}{(-y + y)}} \]
\[ 4y + 0 \le 3 + 0 \]
\[ 4y \le 3 \]
Dividindo ambos os membros por $\color{brown}{4}$, teremos:
\[ \frac{4y}{4} \le \frac{3}{4} \]
\[ y \le \left(\frac{3}{4}\right) \]
\[\bbox[4px,border:2px solid brown]{\color{navy}{ V = \left\{ x \in R | x \le \left({\frac{3}{4}}\right)\right\}}}\]

- $\bbox[5px,border:2px solid brown]{\color{blue}{ 15 – 4x \lt 11 + x}}$
Começamos por adicionar aos dois membros os simétricos $\color{brown}{-x}$ e $\color{brown}{-15}$.
\[\underbrace{\color{maroon}{(15 – 15)}} + \underbrace{\color{blue}{(-4x – x)}} \lt \underbrace{\color{maroon}{(11 – 15)}} + \underbrace{\color{blue}{(x – x)}} \]
\[ 0 – 5x \lt -4 + 0 \] \[ -5x \lt -4 \]
Dividindo ambos os membros por $\color{brown}{-5}$, isolamos $\color{brown}{x}$ e invertemos a desigualdade de $\color{brown}{\lt}$ para $\color{brown}{\gt}$.
\[\frac{-5x}{-5} \lt \frac{-4}{-5} \] \[ x \gt \left(\frac{4}{5}\right) \]
\[\bbox[5px,border:2px solid brown]{\color{navy}{ V = \left\{ x \in R | x \gt \left(\frac{4}{5}\right) \right\}}}\]

- $\bbox[5px,border:2px solid brown]{\color{blue}{ 6x + 5\gt 4x – 7}}$
Para isolarmos $\color{brown}{x}$ no primeiro membro, temos que adicionar aos dois os simétricos de $\color{brown}{4x}$ e $\color{brown}{5}$, ficando assim:
\[\underbrace{\color{blue}{6x -4x}} + \underbrace{\color{maron}{ 5 – 5}} \gt \underbrace{\color{blue}{4x – 4x}} + \underbrace{\color{maroon}{(-7 – 5)}} \]
\[ 2x + 0 \gt 0 – 12 \] \[ 2x \gt -12 \]
Dividimos por $\color{brown}{2}$ ambos os membros e teremos:
\[ \frac{2x}{2} \gt \frac{-12}{2} \] \[ x \gt -6 \]
\[\bbox[5px,border:2px solid brown]{\color{navy}{ V = \{ x \in R | x \gt – 6 \}}} \]

- $\bbox[5px,border:2px solid brown]{\color{blue}{ 2 + 7x \gt 6x + 4}} $
Adicionando $\color{brown}{-2}$ e $\color{brown}{-6x}$ aos dois membros isolamos $\color{brown}{x}$ no primeiro membro.
\[ \underbrace{\color{maroon}{ 2 – 2}} + \underbrace{\color{blue}{7x – 6x}} \gt \underbrace{\color{blue}{6x – 6x}} + \underbrace{\color{maroon}{4 – 2}} \]
\[ 0 + x \gt 0 + 2 \]
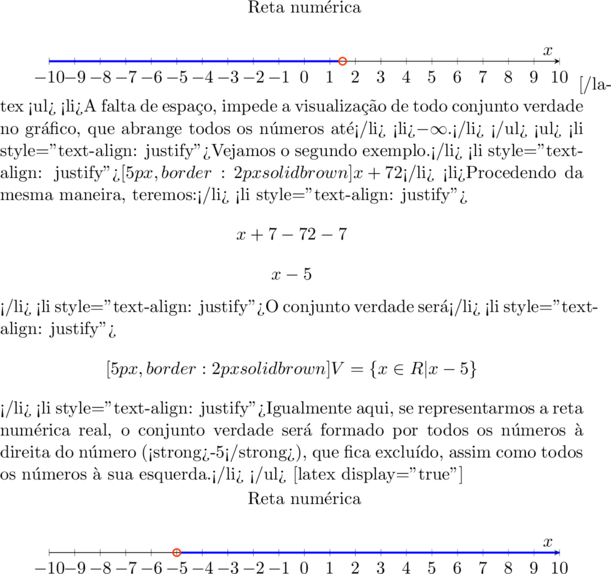
\[ x \gt 2 \]
\[\bbox[5px,border:2px solid brown]{\color{navy}{ V = \{ x \in R| x \gt 2\}}} \]

Curitiba, 02 de junho de 2016
Curitiba, 07 de janeiro de 2018 (Republicação)
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celulares: (41) 99805-0732