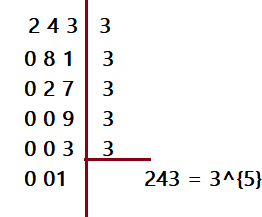Mais umas novidades sobre radiciação.
Multiplicação de radicais de mesmo índice.
- Vamos ver como isso funciona.
- $\color{Blue}{\sqrt[3]{ 5}\times\sqrt [3]{7}\times\sqrt [3]{2} =\sqrt[3]{5\times7\times2} = \sqrt[3]{70}}$
- $\color{Blue}{\sqrt [5]{2^3}\times\sqrt[5]{4^2}\times\sqrt[5]{8} = \sqrt[5]{2^3}\times\sqrt[5]{2^2}^2\times\sqrt[5]{2^3}}$
- $\color{Blue}{ \sqrt[5]{2^3}\times\sqrt[5]{2^4}\times\sqrt[5]{2^3} = \sqrt[5]{2^{3+4+3}}}$
- $\color{Blue}{\sqrt[5]{2^{10}} = 2^{\frac{10}{5}} = 2^2}$
- Podemos notar que é possível resolver uma porção de operações com potências e raízes sem recorrer a nenhum cálculo pesado. Basta aplicar as propriedades que permitem fazer uma variedade de transformações. Dos exemplos deduzimos:
- Uma multiplicação de radicais de mesmo índice é igual a um único radical, com o mesmo índice, cujo radicando é o produto dos radicandos fatores.
Continue lendo “01.014 – Matemática, aritmética, radiciação – propriedades.”