Vamos começar com as divisões exatas, onde não sobram restos. Seja dividir as expressões abaixo.
\begin{align}{(a^3x^3 + 9a^2x^2y + 27axy^2 + 27y^3)}\div {(ax + 3y)}\end{align}
Vamos colocar os polinômios numa chave como fazemos na divisão de números com vários algarismos. Antes vamos verificar se os polinômios estão ordenados segundo os expoentes de uma ou mais variáveis.
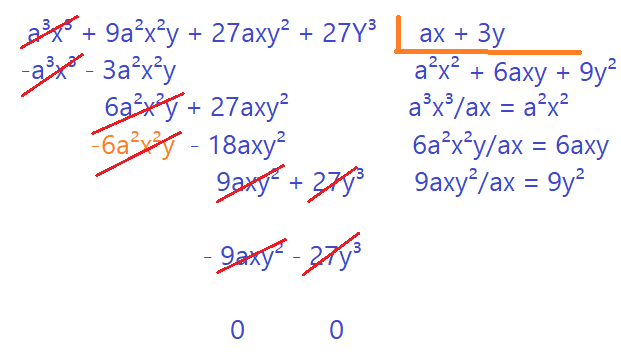
Observe que começamos dividindo o primeiro termo do dividendo pelo primeiro do divisor. Multiplicamos todos os termos do divisor e subtraímos os resultados dos termos semelhantes do dividendo. Fica evidente que no primeiro termo o resto deve ser zero. Na sequência colocamos o outro termo do dividendo ao lado do resto e seguimos o procedimento, até que tenhamos utilizado todos os termos do dividendo. Se o resto for zero, a divisão é exata. Se houver resto, no momento de efetuar a multiplicação do quociente pelo divisor, será necessário adicionar esse resto. No exemplo mostrado, a divisão foi exata.
Podemos então escrever o resultado desse modo:
\begin{align}{(a^3x^3 + 9a^2x^2y + 27axy^2 + 27y^3)}\div{(ax + 3y)}\\= {(a^2x^3 + 6axy + 9y^2)}\end{align}
Vejamos mais um exemplo.
\begin{align}{(3x^3 + 14x^2y + 17xy^2 + 6y^3)}\div{(x + 3y)}\end{align}
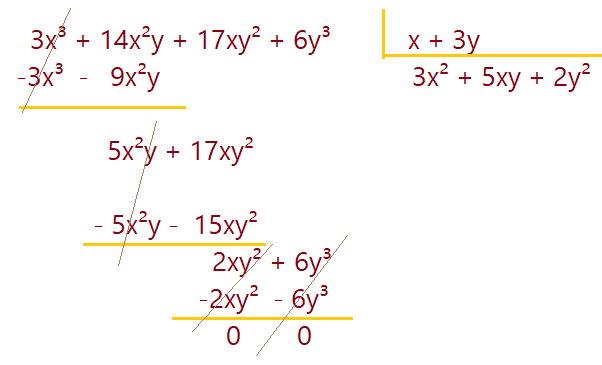
Mais um exemplo de divisão exata entre dois polinômios. Um detalhe a ser sempre levado em consideração é o grau dos polinômios. O divisor nunca poderá ter grau mais elevado do que o dividendo. Isso nos levaria a uma situação impossível de realizar no campo de álgebra.
\begin{align}{(3x^3 +14x^2y + 17xy^2 + 6y^3)}\div{(x + 3y)} \\= {(3x^2 + 5xy + 2y^2)}\end{align}
Vamos ver um exemplo em que a divisão não seja exata.
\begin{align}{(5x^4y + 7x^3y^2 – 8x^2y^3 + 12xy^4)}\div{(x + 3y)}\end{align}
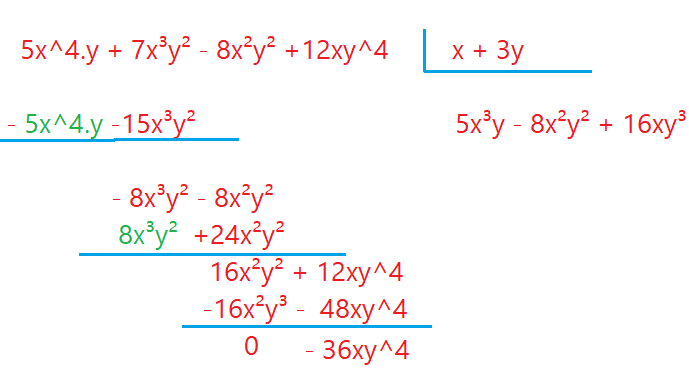
Para fazer o caminho de retorno, teremos que multiplicar o quociente, pelo divisor e adicionar o resto que ficou ao final do processo. Veja como fica:
\begin{align}{(5x^3y – 8x^2y^2 + 16xy^2)}\times{(x + 3y)} + {-36xy^4}\end{align}
Mais um exemplo para confirmar e tirar as dúvidas.
\begin{align}{(x^2 + x^2y – xy^2 – y^3)}\div{(x – y)}\end{align}
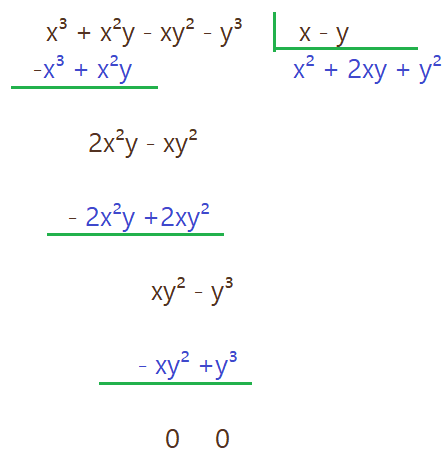
Podemos notar que o quociente e o divisor são fatores que formam um produto notável, que é conhecido como quadrado da soma multiplicado pela diferença. Ele nos ajuda a entender qualquer outra divisão de polinômios entre si.
Chegou a hora de deixar um trabalho para você fazer.
\begin{align}{(x^3 +x^2y – sy^2 – y^3)}\div{(x – y)}\\ = {(x^2 + 2xy + y^2)}\end{align}
Efetue a divisão dos polinômios listados a seguir.
a) \begin{align}{(x^3 – x^2y + xy^2 – y^3)}\div {(x + y)}\end{align}
b)\begin{align}{(8a^3x^3 + 4a^2x^2y – 2axy^2 – y^3)}\div{(4a^2x^2 + 4axy + y^2)}\end{align}
c)\begin{align}{(8a^3x^3 – 4a^2x^2y + 2axy^2 – y^3)}\div{(2ax + y)}\end{align}
d)\begin{align}{(81x^4 – 108x^3y + 48xy^3 – 16y^4)}\div{(9x^2 – 4y^2)}\end{align}
e)\begin{align}{(2a^3 – 11a^2b + 12ab^2 + 9b^3)}\div{(2a + b)}\end{align}
f)\begin{align}{(75x^3 – 160x^2z – 68x^2 – 16z^3)}\div{(5x – 2z)}\end{align}
g)\begin{align}{(3u^3v^3 + 5u^2v^2w + uvw^2 -w^3)}\div{(3uv – w)}\end{align}
h)\begin{align}{(10x^3 + 15x^2y -6xy^2 – 2y^3)}\div{(2x – y)}\end{align}
i)\begin{align}{(8a^3x^3 – 4a^2x^2y 6axy^2 – 3y^3)}\div{(2ax + y)}\end{align}
j)\begin{align}{(2a^3 – 11a^2b + 12ab^2 + 13b^3)}\div{(2a + b)}\end{align}
Havendo dúvidas na resolução, faça contato por meio de um dos canais que estão listados abaixo. Estou disponível para ajudar.
Curitiba, 28 de junho de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

