Buscas na internet.

Pesquisando na internet, descobri que nos últimos dias a procura pelo assunto potenciação, por parte dos internautas, aumentou quase 100%. Isso significa que estou atacando um dos assuntos mais procurados. Vamos seguir mais um pouco. Apresentar mais uns detalhes sobre o assunto.

• Vamos ver como se faz uma multiplicação de potências iguais.
• Assim: $3^2\times 3^2\times 3^2\times 3^2=(3^2{)}^4$
• Temos agora uma potência de potência, isto é, três elevado ao quadrado, elevado a quarta potência.
• Vamos aplicar no começo, a regrinha da multiplicação de potências de mesma base.
• Teremos:$3^{(2+2+2+2)}=3^8$

Se observarmos bem, os expoentes na expressão ${[(3{)}^2]}^4$, vemos que, se multiplicarmos os expoentes $2\times 4=8$ ou seja a soma dos expoentes das potências iguais.

Dessa forma pode-se afirmar que:

• “Para elevar uma potência a outra potência, basta conservar a base e multiplicar os expoentes”.
• Vamos exercitar um pouco?
  • $[(4{)}^2{]}^3=4^{(2\times 3)}=4^6$
  • $[(7{)}^3{]}^3=7^{(3\times 3)}=7^9$
  • $[(11{)}^4{]}^2=(11{)}^{(}4\times 2)=(11{)}^8$
  • $[(5{)}^4{]}^5=5^{(4\times 5)}=5^{20}$

Fica muito simples perceber que a operação potenciação apresenta bem mais possibilidades de aplicações úteis, do que meramente substituir uma multiplicação por uma expressão mais simples, mais curta. Começam a pintar várias novidades. O que vimos até aqui é apenas um pequeno vislumbre do que é possível. Mas vamos devagar. Um degrau de cada vez.

Vamos recordar o que já vimos até aqui?

• Transformar potências em multiplicações de fatores iguais.
  • $7^3=?$
  • $5^2=?$
  • $8^6=?$
  • $3^4=?$
  • $2^5=?$

• Escrever na forma de potências as multiplicações.
  • $3\times 3\times 3\times 3\times 5\times 5\times 5=?$
  • $5\times 5\times 5\times 5\times 5\times 5=?$
  • $4\times 4\times 4\times 4\times 4\times 4\times 4\times 4=?$
  • $11\times 11\times 11\times 11\times 11=?$
  • $7\times 7\times 7\times 7=?$

• Escrever o resultado das potências.
  • $3^3=?$
  • $5^3=?$
  • $2^5=?$
  • $7^1=?$
  • $6^0=?$
  • $(500{)}^0=?$
  • $(50{)}^1=?$

• Efetuar as multiplicações de potências de mesma base.
  • $3^2\times 3^4\times 3^2\times 3^3\times 3^5=?$
  • $5^4\times 5^3=?$
  • $4^0\times 4^3\times 4^5=?$
  • $6^2\times 6^3\times 6^3\times 6^2=?$
  • $7^5\times 7^1\times 7^2=?$

• Efetuar as divisões das potências de mesma base.
  • $(5^8)÷(5^3)=?$
  • $(13{)}^5÷(13{)}^2=?$
  • $(4^7)÷(4^7)=?$
  • $(6^3)÷(6^1)=?$
  • $(8^6)÷(8^5)=?$

• Vamos dar mais um passinho?
  • E se o expoente for uma potência?
  • ${5^3}^2=5^9$
• Trata-se agora de um expoente exponencial. Antes de elevarmos a base ao expoente, precisamos efetuar a potência desse expoente. Ou seja, precisamos efetuar o $3^2=9$ e depois elevar o 5 à nona potência. Teremos então: $5^9$

Note que se multiplicássemos os expoentes ($3\times 2=6$, teríamos $5^{3\times 2}=5^6$, que é totalmente diferente. Notamos que a coisa fica um pouco mais complexa. Portanto cuidado. Potência de potência não é o mesmo que potência com expoente exponencial. Felizmente o uso dessa forma é menos comum, do que a primeira. Um pouco de exercício faz bem, né!

• Efetue as potências indicadas.
  • ${7^5}^2=?$
  • ${5^3}^1=?$
  • ${6^4}^3=?$
  • ${8^3}^4=?$
  • ${9^2}^3=?$
• Transforme os expoentes das potências em exponenciais.
  • $3^{32}=?$
  • $7^{243}=?$
  • $(13{)}^{27}=?$
  • $5^{625}=?$
  • $9^{256}=?$
• Adendo: Um leitor me enviou a seguinte pergunta, ou melhor questão: Realizar a divisão que ele encontrou num livro ou apostila e não entendeu como resolver.

• 

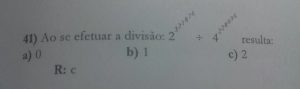
• A divisão apresentada é a divisão de duas potências. Seria assim:
• ${{{{{2^3}^2}^1}^8}^7}^6÷{{{{{4^2}^2}^8}^0}^9}^6$
• Vemos uma sucessão de potências em número de 6 (seis). À primeira vista parece algo difícil de resolver. Se fôssemos desenvolver tudo, iriamos fazer uma montanha de cálculos desnecessários. Não podemos esquecer que a matemática tem alguns atalhos que nos levam à resposta num piscar de olhos. Aquele problema gigante, se resolve num clic.
• Acompanhem o raciocínio. Na potência dividendo, temos no quarto expoente de cima para baixo o número 1(um). Isto significa que iremos elevar 1(um) ao expoente que existir acima dele e o resultado só pode ser 1(um). Continuando vamos ter:
• $2^1=2$
• Para terminar temos $3^2=9$
• Reduzimos o dividendo à potência $2^9$
• No divisor vamos encontrar na terceira posição, do último expoente para baixo. Sabemos que qualquer expoente para 0(zero), resulta igual a 0.
• O próximo expoente é 8, e vamos ter $8^0=1$
• Na sequência temos o expoente 2 e fica $2^1=2$
• Terminamos com $2^2=4$
• Passamos a ter $4^4={(2^2)}^4=2^{2\times 4}=2^8$
• Efetuando a divisão $2^9÷2^8=2^{9-8}=2^1=2$.
• Este resultado comprova que a resposta indicada na figura é a correta.

• Andamos mais um passo. Se você for um dos que procuraram pelo assunto potenciação na internet e tiver interesse em aprofundar o assunto, entre em contato comigo nos endereços que constam abaixo do artigo. Estou a disposição para orientar e tirar suas dúvidas. Legal?

Curitiba, 05 de novembro de 2018.

Décio Adams

decioa@gmail.com

adamsdecio@gmail.com

canalmatfisonline@gmail.com

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celulares: (41) 99805-0732