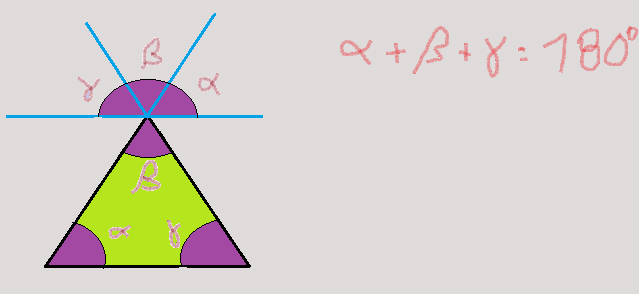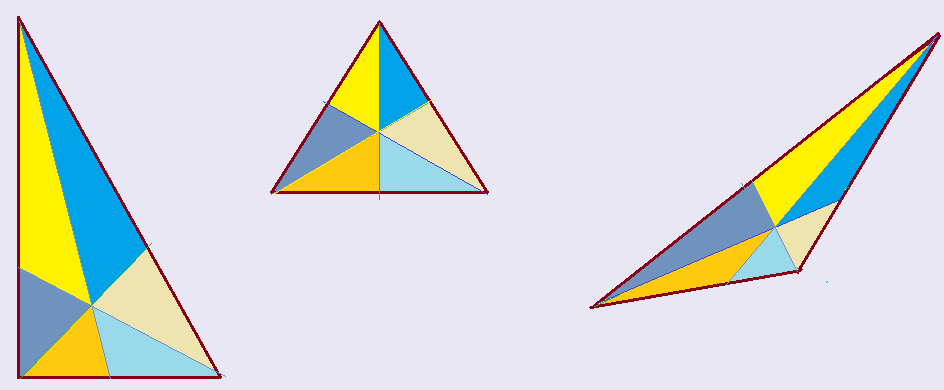Tag: #geometria plana

Publicado em

Matemática – Geometria. Geometria Plana. Polígonos

Hexágono regular

Recapitulando os polígonos regulares vistos até aqui, veremos que em todos eles existe um ponto central, onde ocorre a divisão da circunferência em triângulos congruentes.

No triângulo equilátero temos o baricentro.

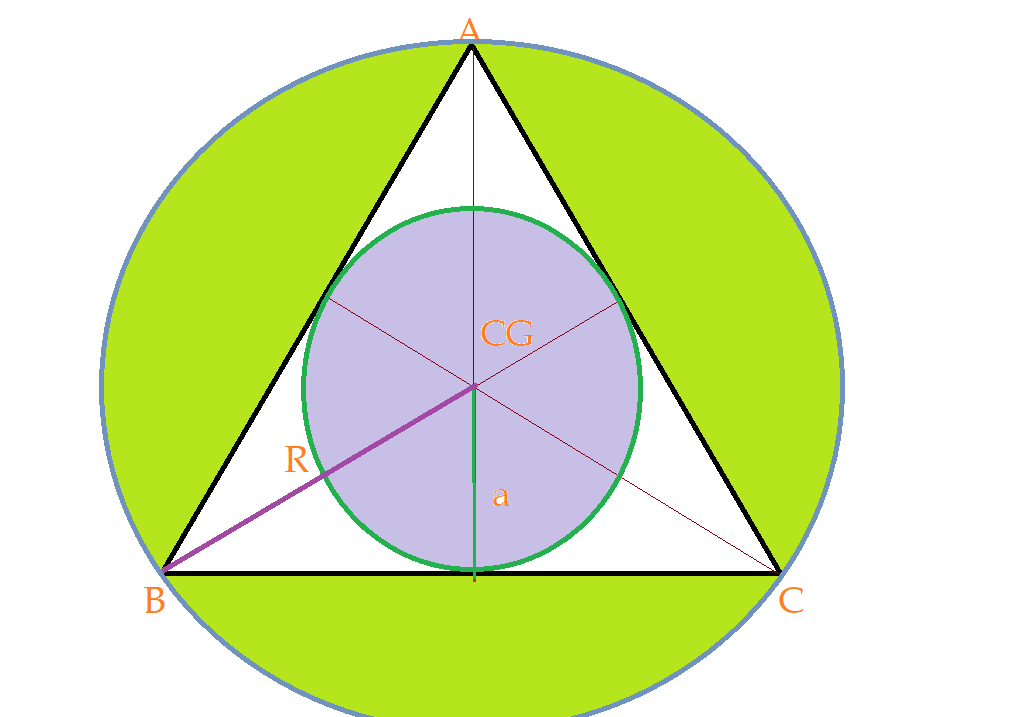
As linhas que unem os vértices ao meio do lado oposto, se interceptam no centro geométrico. Cada lado subtende um ângulo central de 120º, o que perfaz uma volta completa de 360º.

O quadrado tem esse ponto determinado pelas duas diagonais, que são perpendiculares entre si, formando quatro ângulos de 90º.

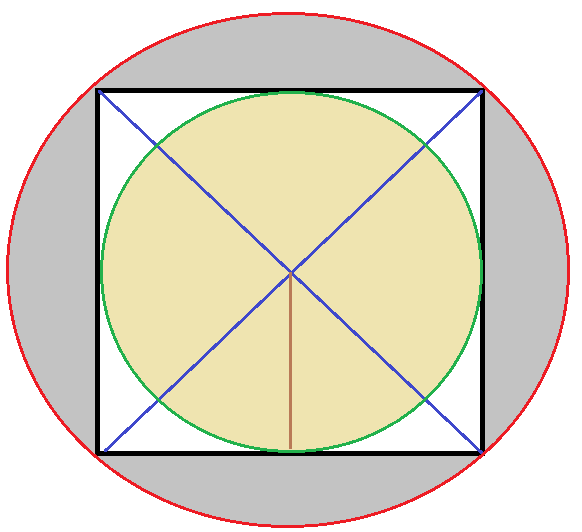
É fácil perceber que as duas diagonais dividem o círculo, tanto inscrito, quanto o circunscrito em quatro partes iguais, cada uma subtendendo um ângulo central de 90º.

O pentágono regular também tem esse ponto. É o centro geométrico do polígono.

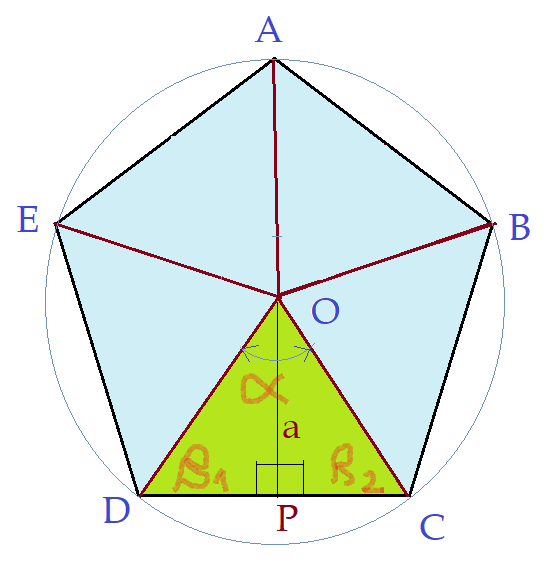
As linhas medianas, que unem os vértices ao meio dos lados opostos, formam cinco triângulos, que têm um vértice comum no ponto de intersecção dessas linhas. Cada um deles mede exatamente 72º.

Hexágono

Seguindo o mesmo critério, as linhas medianas irão dividir o hexágono em seis triângulos equiláteros. Cada um dos ângulos centrais mede então $60^{0}$. Os outros dois ângulos dos triângulos juntos medem $120^{0}$, sendo que são congruentes e portanto medem também $60^{0}$.

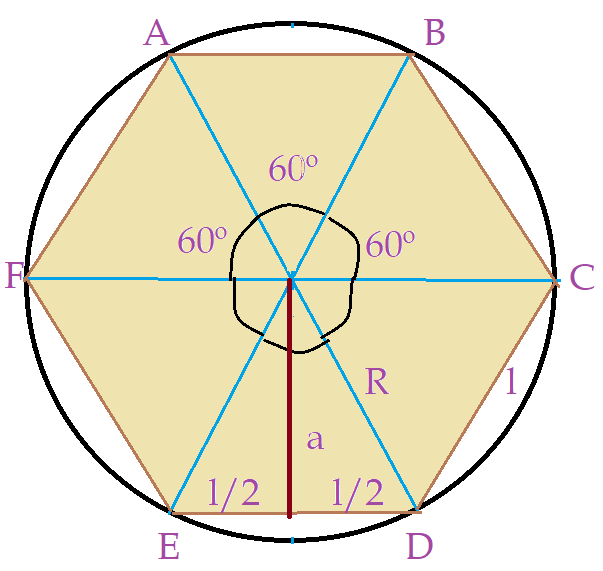
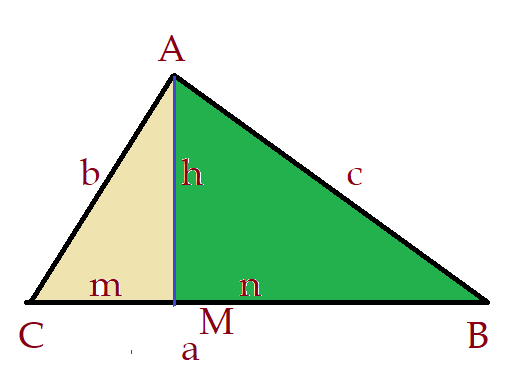
Podemos observar perfeitamente a existência de seis triângulos equiláteros, formando o hexágono regular.

Sendo triângulos equiláteros, sabemos que a altura, neste caso vem a ser o apótema do hexágono; o raio R é congruente ao lado do hexágono. Então podemos determinar o apótema pela expressão:

$ l² = a² + {\left(l\over 2\right)}^{2}$$\Leftrightarrow$$a² = {{4\cdot l² – l²}\over4}$

$\sqrt {a²} = \sqrt{{3\cdot l²}\over4}$

$a = {{l\sqrt{3}}\over 2}$

Área do triângulo e do hexágono.

$S_{\Delta} = {{{{l\cdot l\sqrt{3}}}\over 2}\over 2}$

$S_{\Delta} = {{l²\sqrt{3}}\over4}$

A área do hexágono é a área de um triângulo multiplicado por 6.

$S_{hex} = 6\cdot{l²\sqrt{3}\over4} = 3\cdot{l²\sqrt{3}\over 2}$

Medida dos ângulos internos do hexágono regular.

Cada um dos seis vértices do hexágono é formado por dois ângulos adjacentes de 60^{0}. Isso faz com que cada ângulo interno seja igual a 120^{0}.

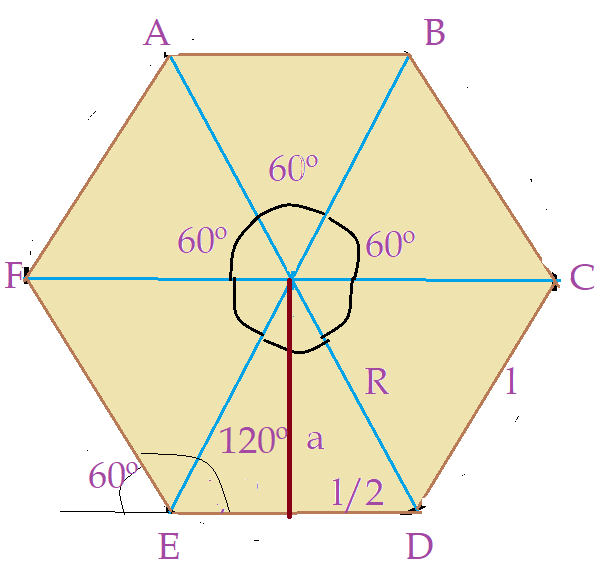
Desta forma a soma dos ângulos internos do hexágono regular é dada por:

$S_{i6} = 6\cdot 120º$

$S_{i6} = 720º$

Círculos inscrito e circunscrito ao hexágono

O lado do hexágono é a medida do raio da circunferência circunscrita e o apótema é a medida do raio da circunferência inscrita. Veja a figura.

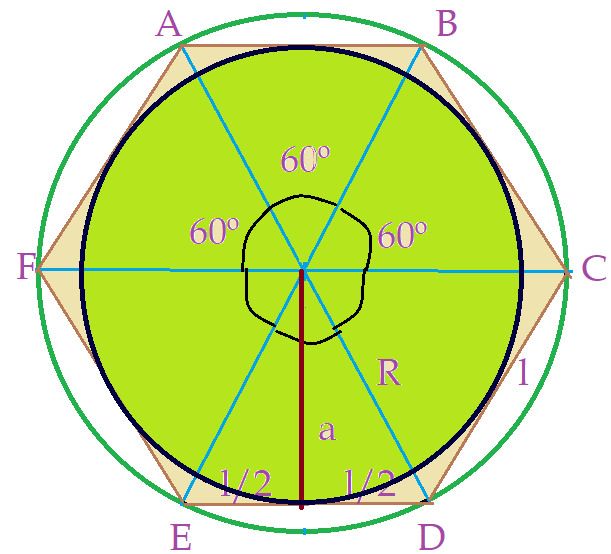
Os dois círculos devidamente traçados, dentro e fora do hexágono.

Exercício 1. Um hexágono tem lado medindo ${l = 2,0 m}$. Determinar: a) o raio da circunferência circunscrita; b) o raio da circunferência inscrita; c) a área de um dos triângulos equiláteros internos; d) a área total do hexágono.

a) o raio da circunferência circunscrita é congruente ao lado do hexágono

${R = 2,0 m}$

b)o raio da circunferência inscrita é o apótema do hexágono.

$a = {{l\sqrt{3}}\over2}$$\Leftrightarrow$$a = {{2\sqrt{3}}\over 2}$

$a = \sqrt{3} m$

c)Temos acima a fórmula da área do triângulo.

$S_{\Delta} = {{l²\sqrt{3}}\over 4}$$\Leftrightarrow$$S_{\Delta}={{2,0}^2\sqrt{3}\over 4}$

$S_{\Delta} = \sqrt{3} m²$

d) a área toda é seis vezes a área do triângulo.

$S_{hex}= {6\cdot{l²\sqrt{3}}\over 4}$

$S_{hex} = {6\cdot\sqrt{3} m²}$

Exercício 2. Um hexágono regular está inscrito em uma circunferência de raio $R = 80,0 cm$. Determinar: a) o lado do hexágono; b) o apótema do hexágono; c) a área de um dos triângulos que formam o hexágono; d) a área total do hexágono;

a)as diagonais que unem os vértices dos ângulos internos opostos, determinam o centro da figura e dividem o hexágono em seis triângulos equiláteros. Assim ficamos com o lado igual ao raio da circunferência.

$l = R$$\Leftrightarrow$$ l = 80,0 cm$

b)o apótema coincide com a altura do triângulo equilátero.

$a = {{l\cdot\sqrt{3}}\over 2}$

$a = {{{80,0}\cdot\sqrt{3}}\over2} = 40,0\sqrt{3}cm$

c)$S_{\Delta} = {{l²\sqrt{3}}\over4}$

$S_{\Delta} = {{{80,0}^{2}\sqrt{3}}\over 4}$$\Leftrightarrow$$ S_{\Delta} = {{{6400,0}\sqrt{3}}\over4} = 1600,0\sqrt{3} cm^2$

d)o hexágono é formado por seis triângulos.

$S_{hex} = 3\cdot{{l^2\sqrt{3}}\over 2}$

$S_{hex} = 3\cdot{{{80,0}^{2}\sqrt{3}}\over2} = {9600,0}\sqrt{3} cm^2$

Heptágono regular

É sem dúvida um dos polígonos com poucos lados que é mais difícil de construir. Isso pelo fato de a divisão dos $360^{0}$ por sete ser um número decimal não exato. Isso torna as medidas dos lados sempre aproximados, bem como os ângulos.

Vejamos

${360 \div 7 = 51,428571…^{0}}$ ou ${51^{0}25’42,857…”}$

Nem mesmo fazendo a divisão em graus, minutos e segundos o resultado é exato, mas difere muito pouco disso.

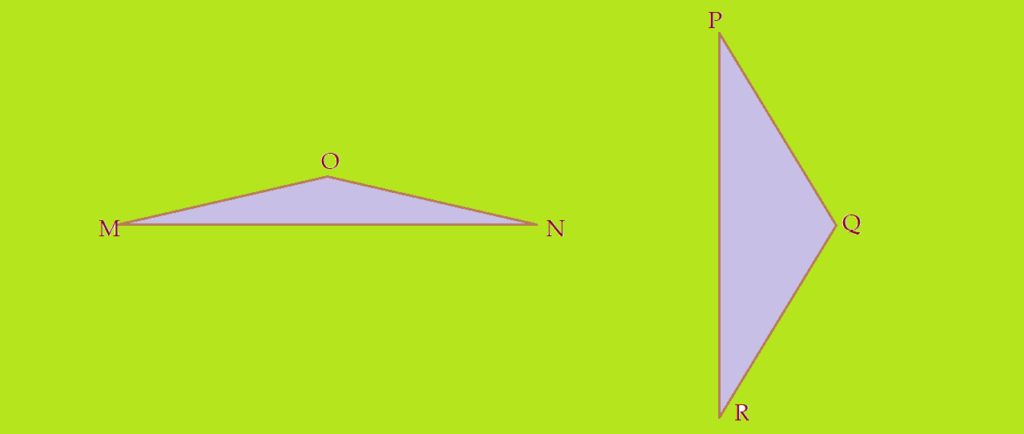
Sabendo que a soma dos ângulos internos de qualquer triângulo é de $180^{0}$, teremos que os dois ângulos restantes de cada triângulo será:

$ {\hat{r} + \hat{s} + \hat{t} = 180^{0}}$

${{(51º25’42,857…”)} + \hat{s} + \hat{t} = 180^{0}}$

Como os dois ângulos são congruentes $\hat{s} = \hat{t}$

${2\cdot\hat{s} = 180º – 51,428571º}$$\Leftrightarrow$${2\cdot\hat{s} = 128,57143º}$

${\hat{s} = 64,28572º}$

Temos aí a dificuldade de construir esse polígono, mesmo usando instrumentos de desenho.

O processo de construção do heptágono regular requer o uso de instrumentos de desenho, como régua, esquadro e principalmente compasso. Usei a ideia aplicando as opções do paint e consegui fazer algo que se aproxima da figura correta.

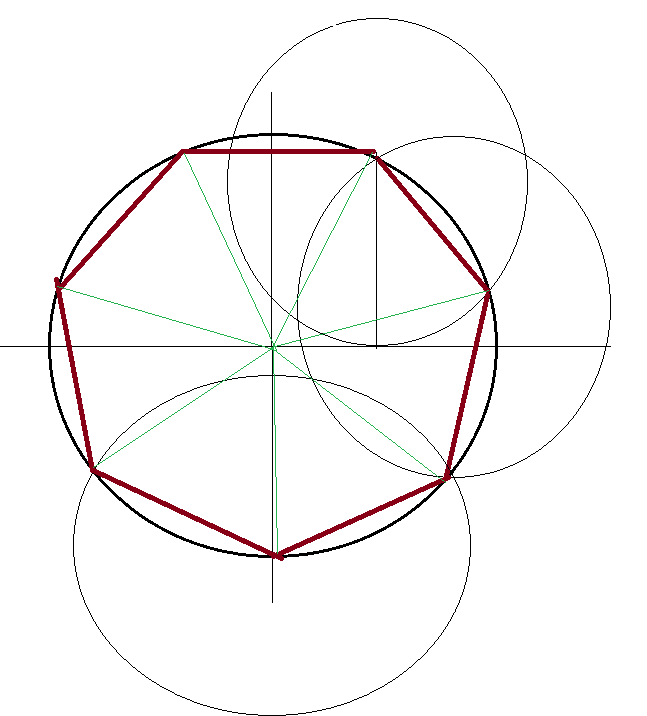
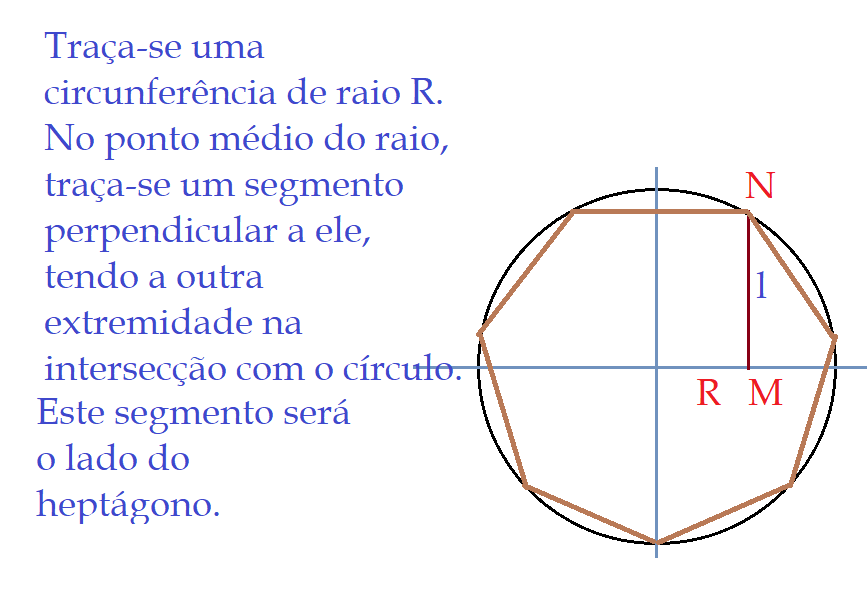
As imprecisões devem-se ao fato de não ser possível manter a exatidão das formas que o programa oferece. Precisamos usar muito de nossa acuidade visual.

O heptágono, traçando-se um segmento que une os vértices ao meio dos lados opostos, fica dividido em sete triângulos isósceles, cujo ângulo central é o determinado acima $51,428571…º$ o que resulta em ângulos de $64,28572…º$ adjacentes aos lados do heptágono. O apótema dividirá esses ângulos internos em dois triângulos retângulos congruentes.

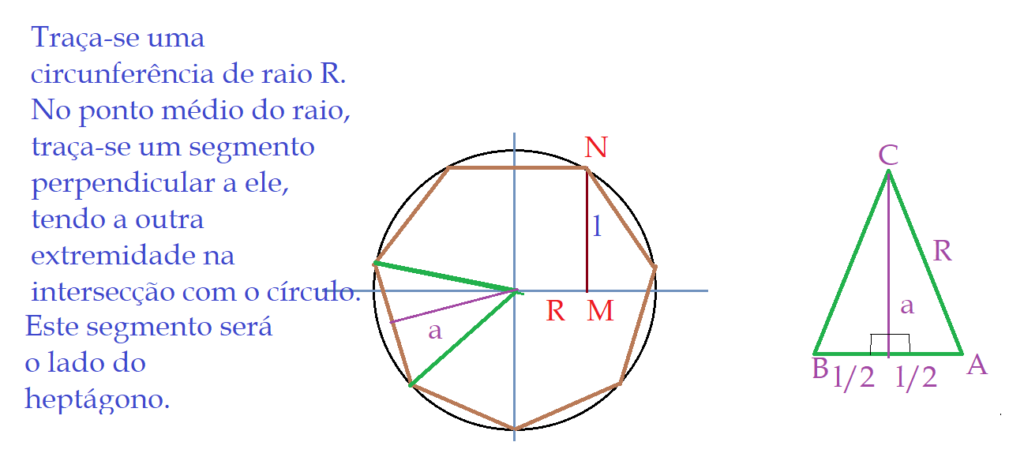
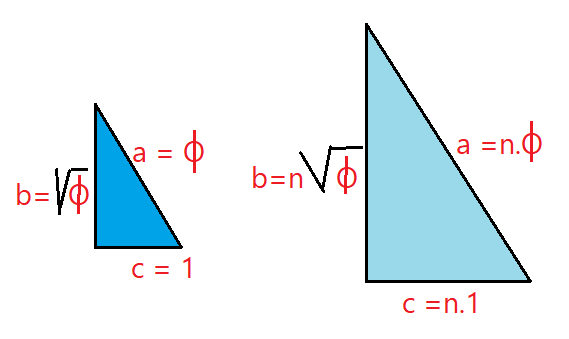
O triângulo ao lado simboliza um dos sete triângulos em que fica dividido o heptágono. Vamos estabelecer a relação entre o lado do polígono e o raio da circunferência, bem como o apótema.

Cada um dos dois triângulos retângulos que obtemos com o traçado do apótema têm como lados o raio R, l/2 e o apótema. R é a hipotenusa. Logo:

${R² = a² +{\left(l\over2\right)}²}$ (I)

${{l\over2} = {R\cdot{cos(64,28572º)}}}$$\Leftrightarrow$${l = 2\cdot{R}\cdot{cos(64,28572º)}}$

${l\simeq {0,868}\cdot{R}}$ (II)

O lado do hexágono é aproximadamente igual a 0,868 R.

Substituindo (II) em (I):

${R^2 = a^2 + \left({{0,868\cdot{R}}\over 2}\right)^{2}}$$\Leftrightarrow$${a^2 = R^2 – {{R^2\cdot{(0,753)}}\over 4}}$

${\sqrt{a^2} = \sqrt{{{4R^2 – 0,753R^2}\over 4}}}$$\Leftrightarrow$$a = \sqrt{{R^2\cdot{(4 – 0,753)}\over 4}}$

$a = R\cdot\sqrt{(3,247)}\over 2 $$\Leftrightarrow$$a = R\cdot{(1,8019)}\over 2$

${a\simeq 0,9R}$

O apótema de um heptágono regular é aproximadamente igual a nove décimos do raio da circunferência circunscrita.

Área de um Heptágono regular

Primeiro vamos estabelecer a área de cada um dos triângulos isósceles que formam um heptágono regular.

A base é o lado: $ l\simeq 0,868 R$

A altura é o apótema: $a\simeq 0,9R$

$S_{\Delta} = {{(0,868)\cdot R}\cdot {(0,9)\cdot R}\over 2}$ $\Leftrightarrow$$S_{\Delta} = {{{0,78}\cdot{R}}\over 2}$

$S_{\Delta} = 0,39R$

Sendo sete triângulos, basta multiplicar o resultado por esse número.

$S_{hep} = 7\cdot{(0,39R)}$$\Leftrightarrow$$S_{hep} \simeq{2,73R}$

Exercício 1. Um heptágono é inscrito num círculo de raio $R = 1,2 m$. Determine: a) o lado do heptágono; b) o apótema do heptágono; c) a área de cada triângulo isósceles que formam o heptágono; d) a área do heptágono.

$R = 1,2 m$

a) $l \simeq 0,868 R$

$l\simeq {0,868}\cdot {1,2}\simeq{1,042} m$

b)$a \simeq {0,9}\cdot {R} $

$a\simeq{0,9}\cdot {1,2}\simeq 1,080 m$

c)$S_{\Delta_{7}}\simeq {0,39}\cdot {R}$

$S_{\Delta_{7}}\simeq {0,39}\cdot{1,2} \simeq{0,468} m²$

d)$S_{hep}\simeq{2,73}\cdot{R}$

$S_{hep}\simeq{2,73}\cdot{1,2}\simeq {3,276} m^2$

Exercício 2. O apótema de um heptágono é igual a $a = 0,50 m$. Determine: a) o lado do apótema; b) a área de um dos triângulos internos; c) o raio do círculo circunscrito ao heptágono; d) a área do heptágono.

$a = {0,50}m$

$a\simeq{0,9}R$$\Leftrightarrow$$ R = {a\over{0,9}}$

a)$l\simeq{0,868}R$$\Leftrightarrow$$l\simeq{0,868}\cdot{{0,50}\over{0,9}}$

$l\simeq {{0,434}\over{0,9}}\simeq{0,482}\, m$

b)$S_{\Delta_{7}} = {0,39}\cdot {a\over{0,9}}$

$S_{\Delta_{7}}= {0,39}\cdot{0,50\over{0,9}}\simeq{0,216} m^2$

c) $a\simeq{0,9}R$

$R \simeq{\left(a\over{0,9}\right)}\simeq\left({0,50}\over{0,9}\right)\simeq{0,556} m$

d)$S_{hep}= {{2,73}\cdot{R}}$$\Leftrightarrow$$S_{hep}\simeq{2,73}\cdot{0,556}$

$S_{hep}\simeq 1,518 m^2$

Diagonais de um polígono

Quantas diagonais podemos traçar em um polígono de n lados?

Vimos que uma diagonal une dois vértices não consecutivos. Assim, tomando um vértice, os dois que lhe ficam consecutivos são excluídos, tal como o próprio vértice. Isso nos permite traçar, a partir de um vértice, tantas diagonais quantos forem os vértices, menos 3:

${D_{v} = n_{v} – 3}$ $\Rightarrow$ diagonais de um vértice.

Cada diagonal une dois vértices, o que nos leva a ter que dividir o número total aparente por dois.

${D_{p} = {{{(n – 3)}\cdot n}\over 2}}$$\Leftrightarrow$$ {D_{p} ={{n² -3n}\over2}}$

Este é o número de diagonais de um polígono. Vamos exercitar!

Exemplo 1. Quantas diagonais tem um pentágono?

${n_{v} = 5}$

${D_{pen} = {{n² – 3\cdot n}\over 2}}$$\Leftrightarrow$${D_{pen}= {{5² -3\cdot5}\over 2}}$

${D_{pen}= {{25 – 15}\over 2}}$$\Leftrightarrow$${D_{pen}= {10\over2} = 5}$

O pentágono tem cinco diagonais.

Exemplo 2. Quantas diagonais tem um quadrado?

${n_{v} = 4}$

${D_{qua}= {{4² – 3\cdot 4}\over 2}}$$\Leftrightarrow$$ {D_{qua}= {{16 – 12}\over 2}}$

${D_{qua} = {4\over 2} = 2}$$\Rightarrow$ quadrado tem duas diagonais.

Exemplo 3. Calcule o número de diagonais de um hexágono.

$ n_{v} = 6 $

${D_{hex}= {{6² – 3\cdot{6}}\over 2}}$$\Leftrightarrow$${D_{hex} = {{36 – 18}\over 2}}$

${D_{hex}= {18\over 2} = 9}$$\Rightarrow$ o hexágono tem 9(nove) diagonais.

Exemplo 4. Quantas diagonais tem um dodecágono?

${n_{v} = {12}}$

${D_{12} = {{(12)^2 – 3\cdot {12}}\over2}}$$\Leftrightarrow$${D_{12}={{144 – 36}\over 2}}$

${D_{12} = {{144 – 36}\over 2}$$\Leftrightarrow$${D_{12} = {{108}\over 2} = 54}$ – O dodecágono tem 54 diagonais.

Exemplo 5. Quantas diagonais possui um polígono de 20 lados?

$n_{v} = 20$

$D_{20}= {{20}^2 – 3\cdot{20}}\over 2}$$\Leftrightarrow$$D_{20} = {{400 – 60}\over 2}$

$D_{20}={{340}\over 2} = 170$

O polígono de 20 lados admite 170 diagonais.

Soma dos ângulos internos de um polígono.

Vimos que as diagonais dividem o polígono em triângulos isósceles, que se inscrevem em um círculo com o qual coincidem os vértices. Dessa forma os ângulos centrais, que tem vértice no centro do círculo, tem a medida obtida pela divisão da volta completa pelo número de lados.

$\hat{a}_{c} = {360\over n}$

Prolongando um lado além do vértice, temos um ângulo externo, que têm a mesma medida do ângulo central dos triângulos. Cada ângulo interno é suplementar do ângulo central dos triângulos.

$\hat{a}_{i} = {180º – \hat{a}_{c}}$$\Leftrightarrow$$\hat{a}_{i} = 180^{0} – {360^{0}\over n}$

$\hat{a}_{i} = {{{180^{0}\cdot n} -360^{0}}\over n}$

A soma dos ângulos internos é igual a medida de um ângulo interno multiplicada pelo número de vértices, que é igual ao número de lados.

$S_{a_{i}} = n\cdot{180^{0} – {360^{0}\over n}}$

$S_{a_{i}}= {180^{0}\cdot n – 360^{0}}$

Exemplo 1. Qual é a soma dos ângulos internos de um polígono de nove lados?

$S_{a_{9}} = {180^{0}\cdot n – 360^{0}}$

$S_{a_{9}} = 180^{0}\cdot 9 – 360^{0}$

$S_{a_{9}}= 1620^{0} – 360^{0} = 1240^{0}$

Exemplo 2. Determine a soma dos ângulos internos de um polígono de 12 lados.

$S_{a_{12}} = 180º\cdot 12 – 360 $

$S_{a_{12}} = 2160º – 360º = 1800º$

Exercícios para resolver.

01. Os hexágonos são polígonos que apresentam seis lados, seis ângulos internos e seis vértices. A respeito dos hexágonos regulares inscritos em uma circunferência, assinale a alternativa correta.

a) Um hexágono é chamado regular quando ele possui ângulos iguais, lados congruentes e não existe a necessidade de que seja convexo para isso.

b) Um hexágono regular inscrito tem a medida do apótema igual à medida do raio do círculo que o circunscreve.

c) Um hexágono regular inscrito tem a medida do lado igual à medida do raio do círculo que o circunscreve.

d) Um hexágono regular é chamado inscrito quando todos os seus lados são tangentes a uma circunferência.

e) Um hexágono regular inscrito possui apótema e lado iguais.

02. Qual é a medida do lado $l$ de um hexágono regular cujo apótema mede$a = 3,0 cm$?

a) $2\sqrt{3} cm$

b) $2 cm$

c) $\sqrt{3} cm$

d) $3\sqrt{3} cm$

e) $6\sqrt{3} cm$

03. Determine a medida do apótema de um hexágono regular, sabendo que a medida de seu lado é igual a $l =2\sqrt{3} cm.

a) $2\sqrt{3} cm$

b)$1 cm$

c) $2 cm$

d) $3 cm$

e) $\sqrt{3} cm$

04. Determine a medida do apótema de um hexágono regular inscrito em uma circunferência de diâmetro igual a $D= 12 cm$.

a) $2\sqrt{3} cm$

b) $3\sqrt{2} cm$

c) $3\sqrt{3} cm$

d) $6\sqrt{2} cm$

e) $6\sqrt{3} cm$

05. (FUVEST-2014). Uma das piscinas do Centro de Práticas Esportivas da USP tem o formato de três hexágonos regulares congruentes, justapostos, de modo que cada par de hexágonos tem um lado em comum, conforme representado na figura abaixo. A distância entre lados paralelos de cada hexágono é de 25 metros.

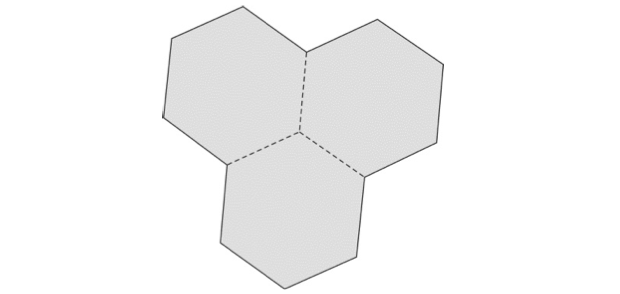
Modelo de piscina (Foto: Reprodução/Fuvest)

Assinale a alternativa que mais se aproxima da área da piscina.

a) $S\simeq1600 m²$;

b)$S\simeq1800 m²$;

c)$S\simeq2000 m²$;

d)$S\simeq2200 m²$

e)$S\simeq2400 m²$

06. Determine o apótema de um hexágono regular cujo lado mede $l = 200\sqrt{3}cm$. Depois calcule a área do hexágono.

07. Determine a área de um hexágono regular cujo lado mede $l = 4,0 cm$. Determine o perímetro desse polígono.

Havendo dúvidas, pergunte. Os canais estão à disposição para quando você precisar.

Curitiba, 15 de novembro de 2019

Décio Adams

[email protected]  

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

Publicado em

Matemática – Geometria plana – Polígonos diversos

Trapézio

É um quadrilátero que tem pelo menos dois lados paralelos, sendo os outros inclinados em relação a eles.

Na figura temos dois trapézios isósceles, onde os lados não paralelos são congruentes e dois que são retângulos em uma extremidade. São dois ângulos retos, um agudo e outro obtuso. Nos primeiros são dois agudos e dois obtusos.

O perímetro é a soma dos quatro lados. Os lados paralelos são geralmente denominados bases, sendo um a base maior e o outro a base menor.

Há também os trapézios escalenos, onde os lados não paralelos não são congruentes e todos os seus ângulos são diferentes entre si.

Diagonais dos trapézios, como nos outros polígonos, unem dois vértices não consecutivos. No caso dos trapézios isósceles elas são congruentes.

Os ângulos adjacentes às bases são congruentes para cada uma das duas bases.

Área do trapézio

É sempre possível determinar uma base média, entre as bases maior e menor. Isso permite formar um retângulo cujo comprimento é a média das bases e o outro lado é a altura do trapézio. Assim:

$S_{t}= {{{B + b}\over2} \cdot h}$

A área do trapézio é igual à média das bases multiplicada pela altura.

  1. Um trapézio isósceles tem os lados paralelos medindo $B= 8,0 cm$ e o outro $b= 4,0 cm$. A altura do polígono é de $h=3,0 cm$. Determine a área deste trapézio.

$S_{t}= {{{B + b}\over2} \cdot h}$

$S_{t}={{{{8,0}+{4,0}}\over{2}}\cdot {3,0}}$

$S_{t}= {6,0}\cdot{3,0} = 18,0 cm²$

2. Um trapézio isósceles, mede em sua base maior $B = 30,0 cm$. Se os ângulos que os lados oblíquos formam com a base são de $\theta = 45º$, quanto medem os ângulos obtusos que eles formam com a base menor? Se a altura é $h=10,0 cm$, quanto medem os lados não paralelos e qual é a área do trapézio?

Os lados não paralelos são duas transversais que interceptam duas retas paralelas. Formam de cada lado um par de ângulos alternos internos. Estes são, como vimos no estudo desse assunto, ângulos suplementares. Portanto: Um trapézio isósceles, mede em sua base maior $B = 30,0 cm$. Se os ângulos que os lados oblíquos formam com a base são de $\theta = 45º$, quanto medem os ângulos obtusos que eles formam com a base menor. Se a altura é $h=10,0 cm$, quanto medem os lados não paralelos e qual é a área do trapézio?

Os lados não paralelos são duas transversais que interceptam duas retas paralelas. Formam de cada lado um par de ângulos alternos internos. Estes são, como vimos no estudo desse assunto, ângulos suplementares. Portanto:

$â + 45º = 180º$ $\Leftrightarrow$$â = 180º – 45º$

$â = 135º$

$\overline{MP} = c$

A base da altura do trapézio determina um cateto do triângulo retângulo. Como a altura é o outro cateto, temos que os dois tem a mesma medida.

$c² = h² + b²$$\Leftrightarrow$$ c² = {10,0}² + {10,0}²$

$c² = 100,0 + 100,0$$\Leftrightarrow$$c = \sqrt{200}$

$c = 10\sqrt{2}cm$

Área: $S= {{30,0 + 10,0}\over2}\cdot 10$

$S = {40,0\over2}\cdot 10$$\Leftrightarrow$$ S = 200,0 cm²$

3. Dada a figura poligonal a seguir:

A figura é composta de dois trapézios retângulos e um triângulo, cuja área é fornecida. Observe e determine o que pede o exercício.

Sendo a área do triângulo $\Delta{(AEDA)}$ igual a $S=800,0cm²$ e é de $3\over 5$ a razão entre as áreas dos triângulos $\Delta{(AMEA)}$ e $\Delta{((DMED)}$ determine:

a)primeiramente a altura $\overline{ME}$ do triângulo;

$S_{\Delta} = {{b\cdot h}\over2}$$\Leftrightarrow$$800,0 = {{80\cdot h}\over2}$

${{{800,0}\cdot{2}}\over{80,0}} = h$$\Leftrightarrow$$ h = 20,0 cm$

b)conhecendo o segmento $\overline{ME}$, podemos determinar o segmento $\overline{EN}$;

$\overline{MN} – \overline{ME} = \overline{EN}$$\Leftrightarrow$$50,0 – 20,0 = \overline{EN}$

$\overline{EN} = 30,0 cm$

c)determine a área do retângulo $S_{ret}{(ABCDA)}$ e depois subtraia dessa área a do triângulo.

$S_{ret} = l\cdot c$$\Leftrightarrow$$S_{ret}= {50,0}\cdot{80,0}$

$S_{ret}= 4000,0 cm^2$

$S = S_{ret} – S_{\Delta}$$\Leftrightarrow$$ S = 4000,0 – 800,0$

$S = 3200,0 cm^2

d)determine os segmentos $\overline{AM} = m$ e $\overline{MD} = n$ que são as alturas dos trapézios ${(ABNEA)}$ e ${(BCNEB)}$.

$S_{\Delta_{1}} = {{m\cdot 20}\over 2}$

$S_{\Delta_{2}} = {{n\cdot20}\over 2}$

${ S_{\Delta_{1}}\over S_{\Delta_{2}}} = {{{{m\cdot 20}\over 2}}\over{{n\cdot20}\over 2}} = {3\over5}$

${ S_{\Delta_{1}}\over S_{\Delta_{2}}} = {{{{m\cdot 20}\over 2}} \cdot{{2\over{n\cdot20}}}} = {3\over 5}$

Simplificando os fatores comuns

${ S_{\Delta_{1}}\over S_{\Delta_{2}}} = {m\over n} = {3\over 5}$

$m = {{3\cdot n}\over5}$ (I)

$m + n = 80$$\Leftrightarrow$$m = 80 – n$ (II)

Substituindo (I) em (II);

$80 – n = {3n\over5}$$\Leftrightarrow$$ 5\cdot{(80 – n)} = 3n$

$400 – 5n = 3n$$\Leftrightarrow$$800 = 3n + 5n$

$8n = 400$$\Leftrightarrow$$n = {400\over8} = 50,0cm$ (III)

Substituindo (III) em (II)

$m = 80 – 50 = 30,0\,cm$

Área do trapézio $S = {{B + b}\over2}\cdot h$

$S_{1} = {{50,0 + 30,0}\over2}\cdot 30$$\Leftrightarrow$$S = 1200,0\, cm^2$

$S_{2}= {{50 + 30}\over 2}\cdot 50$$\Leftrightarrow$$S_{2}= 2000,0\, cm^2$

$S_{1} + S_{2} = 2000,0 + 1200,0 = 3200,0\, cm^2$

Exercícios para resolver

01. Calcule a área de um trapézio de altura 5 cm e bases de 8 cm e 3 cm.

02. Determine a medida da base menor de um trapézio de 100 cm2 de área, 10 cm de altura e base maior de 15 cm.

03. Qual a altura de um trapézio com área de 50 cm2, base maior de 6 cm e menor de 4 cm?

04. Calcule a área de um trapézio de bases medindo 10 cm e 5 cm e altura 6 cm.

05. Determine a medida da base maior de um trapézio com 150 cm2 de área, 10 cm de altura e base menor medindo 12 cm.

06. Num trapézio de 8,0 cm de altura, a base maior é o dobro da base menor. Determine a medida dessas bases sabendo que a área desse trapézio é 180 cm^2.

07. Determine a altura de um trapézio de $45,0\, cm^2$ de área, base maior medindo 11.0 cm e base menor com 7,0 cm de comprimento.

08. Calcule a área colorida em azul da figura abaixo, usando as áreas do retângulo e do trapézio.

A figura é um retângulo do qual foi recortado um trapézio. Basta usar as duas fórmulas de cálculo das áreas e calcular a diferença.

09. Analise a figura poligonal e divida-a em partes das quais seja possível calcular a área e obter o total da área da figura.

É possível dividir a figura de várias formas em polígonos cujas áreas temos capacidade de calcular. A soma dessas áreas será a área da figura.

10. A figura é composta por dois polígonos. Determine as suas áreas e a área total da figura.

Havendo dúvidas, recorra por meio de um dos canais abaixo para esclarecer. Não tenha acanhamento.

Curitiba, 06 de novembro de 2019.

Décio Adams

[email protected]  

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732



Publicado em

Matemática – Geometria – Geometria Plana.

Linhas Poligonais

Linhas poligonais abertas são as linhas em que as extremidades não se tocam. Podem ser curvas, segmentos de reta, um tendo extremidade comum com o seguinte.

A linha não fecha, isto é, não forma uma área delimitada em seu interior.

As linhas poligonais fechadas formam o que denominamos geralmente de figuras geométricas ou polígonos. Esse nome vem do grego: poli = mais de dois e gono = ângulo. Então a figura fechada com mais de dois ângulos é um polígono.

O polígono com menor número de lados é o triângulo, depois vêm os quadriláteros, os pentágonos, hexágonos e assim sucessivamente. O polígono com um número infinito de lados é uma circunferência ou pode ser uma elipse também.

Polígonos regulares e irregulares

Regulares são os polígonos formados por lados iguais. Os lados são os segmentos de reta compreendidos entre dois ângulos consecutivos.

Irregulares são os polígonos formados por lados cujas medidas não são iguais.

Triângulos

Triângulo equilátero, que é também equiângulo é todo triângulo formado por três lados congruentes e em consequência os ângulos internos também são congruentes. Esses ângulos são todos agudos, isto é, medem menos de $90^{0}$.

É o único triângulo que podemos classificar como um polígono regular. Seus lados são congruentes e seus ângulos internos também.

Triângulo isósceles: – é o triângulo que tem dois lados congruentes. A altura, traçada em relação ao lado oposto, divide o triângulo em dois triângulos retângulos congruentes.

O ângulo formado pelos lados congruentes pode ser agudo, reto ou obtuso.

Triângulo escaleno: – é o triângulo que tem os três lados com medidas diferentes. Pode ser retângulo, acutângulo ou obtusângulo.

Triângulo retângulo: – tem necessariamente um ângulo reto, podendo os outros dois ser congruentes ou diferentes, mas sempre menores que$90^{0}$

Os lados do ângulo reto são denominados catetos e o terceiro lado, maior, que é oposto ao ângulo reto, denomina-se hipotenusa.

Triângulo obtusângulo: – tem um ângulo obtuso, sendo os outros dois agudos.

Os triângulos obtusângulos podem ser escalenos ou isósceles. É essencial que um dos três ângulos internos seja maior que $90^{0}$.

Soma dos ângulos internos do triângulo.

Vejamos a figura .

Prolongando dois lados e no vértice traçando uma paralela ao outro lado, formamos dois ângulos correspondentes aos ângulos da base e um que é oposto pelo vértice ao terceiro. Pela figura vemos que esses três ângulos somados totalizam $180^{0}$. Essa soma é sempre a mesma, para qualquer triângulo.

Como podemos observar na figura, os ângulos formados pelos prolongamentos dos dois lados e a paralela ao outro lado, passando pelo vértice oposto a ela, são respectivamente opostos pelo vértice e os outros dois são ângulos correspondentes, formados por uma transversal a retas paralelas. Os três ângulos completam exatamente um ângulo raso, ou seja $180^{0}$. Isso irá ocorrer com qualquer triângulo, não importando as medidas de seus ângulos internos. A soma dos mesmos será sempre a mesma. Dará $180^{0}$.

Podemos estabelecer que:

$\alpha \lt(\beta + \gamma)$

$\beta \lt (\alpha + \gamma)$

$\gamma \lt (\beta + \alpha)$

Também podemos estabelecer que cada ângulo é maior do que o módulo da diferença dos outros dois.

$\alpha \gt |\beta – \gamma|$

$\gamma \gt |\alpha – \beta|$

$\beta \gt |\alpha – \gamma|$

Segmentos notáveis num triângulo

Altura: – é o segmento que une um vértice ao lado oposto formando com ele um ângulo reto. Como mostram as várias figuras, esse segmento pode estar localizado no interior do triângulo, como também pode estar fora, como acontece nos ângulos obtusângulos, quando é traçada em relação a um dos lados menores. Nos triângulos retângulos, as alturas em relação aos catetos, são os próprios. As alturas traçadas em relação aos três lados, se interceptam em um ponto, que pode estar localizado fora da figura. Este ponto é o chamado ortocentro do triângulo

Habitualmente a altura é simbolizada pela letra h, o que não é regra, apenas uma sugestão. A intersecção das alturas é denominada de ortocentro do triângulo.

Bissetriz: – denominamos bissetriz a reta ou segmento de reta que divide um ângulo ao meio. Todo triângulo possui três bissetrizes, que se interceptam em um ponto, no interior do polígono. A intersecção das bissetrizes denomina-se incentro, isto é, centro do compasso nesse ponto e abertura até qualquer um dos lados, pode-se traçar uma circunferência inscrita no interior do triângulo. Ela será tangente aos três lados do triângulo.

As bissetrizes inscrevem uma circunferência no interior do triângulo. Esta circunferência toca os três lados do triângulo.

Obs.: O triângulo equilátero e equiângulo, é o único triângulo que pode ser denominado como figura geométrica regular. Por isso dedicaremos especial atenção a alguns detalhes. (Final.)

Medianas de um triângulo: – denominamos medianas as retas ou segmentos de reta que contém um vértice e o ponto médio do lado oposto a esse vértice, em qualquer triângulo. A intersecção das medianas determina o ponto denominado baricentro. Em outras palavras significa que uma lâmina triangular de material e espessura uniforme fica em equilíbrio se suspensa por esse ponto.

A intersecção das medianas determina o centro de massa de uma lâmina em forma de triângulo, sendo feita de material uniforme e espessura constante.

Mediatrizes de um triângulo: – são segmentos de reta levantados perpendicularmente ($90^{0}$) ao ponto médio de cada um dos lados do triângulo. A intersecção desses segmentos determina o ponto denominado circuncentro. Centrando o compasso nesse ponto e com abertura aos vértices, pode-se traçar uma circunferência circunscrita ao triângulo.

As mediatrizes permitem circunscrever uma circunferência ao triângulo, contendo os três vértices.

Triângulos semelhantes

Dois ou mais triângulos são semelhantes se eles tiverem ao menos dois ângulos congruentes. Como a soma dos ângulos internos de qualquer triângulo é sempre igual a $180^{0}$, a congruência entre dois ângulos, implica necessariamente que o terceiro ângulo também seja congruente.

Os triângulos semelhantes têm uma característica importante. A congruência entre seus ângulos faz com que os lados que formam os respectivos ângulos sejam proporcionais.

Aqui temos dois triângulos equiláteros e portanto são semelhantes. Não são congruentes pois seus lados têm medidas diferentes, porém eles são proporcionais.

Observando os lados correspondentes podemos escrever a proporção:

$ {a\over a’} = {b\over b’} = {c\over c’}$

Agora temos dois triângulos retângulos, onde os ângulos congruentes determinam a proporcionalidade entre os lados correspondentes.

${m\over m’} = {n\over n’} = {p\over p’}$

Temos aqui um triângulo retângulo, onde a altura $h$ divide o ${\Delta}{(ABCA)}$ em dois triângulos semelhantes entre si e ao original.

No triângulo retângulo, temos o angulo reto $\widehat{(BAC)}$, e os ângulos agudos $\widehat{(ABC)}$ e $\widehat{(ACB)}$. Ao traçar a altura $h$ passamos a ter dois triângulos retângulos com os ângulos retos adjacentes $\widehat{(AMB)}$ e $\widehat{(AMC)}$. Tanto o $\Delta{(AMBA)}$ quanto o $\Delta{(AMCA)}$ têm um ângulo comum com o $\Delta{(ABCA)}$. Sendo assim ambos são semelhantes ao triângulo maior e consequentemente são semelhantes entre si. Isso nos permite escrever a proporção:

${m\over h} = {h\over n}$$\Leftrightarrow$$ h² = m\cdot n$

Entre estas expressões a que mais usamos em aplicações variadas é a última, que costuma ser enunciada como:

“Num triângulo retângulo a altura relativamente à hipotenusa é média proporcional entre as projeções dos catetos sobre ela”.

Como demonstramos acima.

Triângulo áureo

O triângulo áureo básico é aquele que tem por hipotenusa um segmento cuja medida é igual à razão áurea $a = \Phi$. Os catetos são $b = \sqrt{\Phi}$ e $c = 1$. Todos os triângulos semelhantes a esse, quer sejam maiores ou menores são triângulos áureos. Seus lados serão respectivamente proporcionais.

Triângulo áureo fundamental e seus semelhantes

Podemos determinar os ângulos internos de qualquer triângulo áureo.

Por definição o ângulo entre os lados menores é reto. Mede $90^{0}$.

Os ângulos agudos são opostos aos catetos. Vejamos:

$sen^{-1}\gamma = \frac{\sqrt{\Phi}}{\Phi} = \frac{\sqrt{1,618}}{1,618}$

$\color{Navy}{sen^{-1}\gamma\simeq 51,828^{0}}$

$sen^{-1}\alpha = \frac{1}{\Phi} = \frac{1}{1,618}$

$\color{Navy}{sen^{-1}\alpha\simeq 38,172}$

Soma dos lados de um triângulo

Perímetro: – é a soma dos três lados do triângulo.

$p_{\Delta} = a + b + c$

Soma de dois lados: – em qualquer triângulo a soma de dois lados será sempre maior do que o terceiro lado.

$a \lt b + c$

$b \lt a + c$

$c \lt a + b$

Diferença entre dois lados: – o módulo da diferença entre dois lados de um triângulo é sempre menor do que o outro lado.

$|a – b| \lt c$

$|a – c| \lt b$

$|b – c| \lt a$

O triângulo retângulo tem uma característica importante, que veremos no próximo post. É uma figura geométrica de grande importância, com inúmeras situações em que se aplicam os conhecimentos a seu respeito.

Algumas perguntas para pensar?

  1. Um triângulo retângulo pode ser equilátero?

( ) sim; ( ) não; Porquê?…………………………………

2. Um triângulo escaleno pode ser retângulo?

( ) sim; ( ) não; Porquê?………………………………

3. Um triângulo equilátero pode ser obtusângulo?

( ) sim; ( ) não; Porquê? ……………………………………

4. Um triângulo isósceles pode ser retângulo?

( ) sim; ( ) nâo; Porquê? …………………………………

5. Um triângulo isósceles pode ser obtusângulo?

( ) sim; ( ) não; Porquê?…………………………………..

06. Um triangulo equilátero e um obtusângulo podem ser semelhantes? ( ) sim; ( )não; Porquê? ……………………………………………………………………………..

07. Se um triângulo deve ser construído com os lados medindo 3,0 cm, 5,0 m e 10,0 cm, é possível essa construção? ( )sim; ( )não; Porquê? Pense bem antes de responder. ………………………………………………………………………………………………..

08. Se a hipotenusa de um triângulo áureo mede $a = 5,0\,cm$, quais são as medidas de seus catetos?

09. O cateto menor de um triângulo áureo mede $c = 3,2\,cm$. Determine a medida do outro cateto e da hipotenusa.

10. A soma dos catetos de um triângulo áureo mede $b + c = 6,0\,cm$. Determine as medidas dos catetos e também da hipotenusa.

11. Um triângulo tem os lados $a = 8,0\, cm$ e $b= 6,0\,cm$. O terceiro lado mede tem sua medida em qual intervalo?

12. Em um triângulo um dos lados mede $15,0\,cm$. Quais os possíveis valores das medidas dos outros dois lados?

13. Se um dos ângulos de um triângulo mede $75^{0}$, quais são os possíveis valores das medidas dos outros dois ângulos?

14. Se um triângulo retângulo tem um ângulo agudo de $52^{0}$, quantos graus mede o outro ângulo agudo?

15. Se dois ângulos em um triângulo medem respectivamente $48^{0}$ e $62^{0}$, qual é a medida do terceiro ângulo?

16. Um triângulo tem dois lados medindo $a = 25,0\,cm$ e $b = 32,0\,cm$. Pergunta-se qual é o valor máximo que o perímetro desse triângulo pode ter?

Se ficaram dúvidas, faça a gentileza de entrar em contato por meio de um dos canais listados abaixo e vamos esclarecer o que não ficou entendido. OK?

Curitiba, 26 de outubro de 2019

Décio Adams

[email protected]  

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e Whatsapp: (41) 99805-0732

Publicado em

Matemática – Geometria

Introdução.

O desenvolvimento dos conceitos geométricos foram ocorrendo ao longo da história, especialmente para suprir as necessidades construtivas, demarcações de áreas e outras atividades humanas em sua evolução.

Há evidências do uso de algumas formas geométricas desde a mais remota antiguidade, grandemente nas inscrições denominadas rupestres, nas grutas e cavernas. Eram lugares primitivamente usados para abrigar os seres humanos das intempéries e outros riscos que enfrentavam.

De época mais recente, uma boa parcela de formas geométricas e mesmo alguns cálculos rudimentares, surgiram entre os egípcios para construção de seus sistemas de irrigação agrícola, bem como a demarcação periódica dos lotes destinados ao plantio, após as enchentes benfazejas do Rio Nilo. Foi um filósofo/matemático grego, de nome Euclides, que colocou ordem no caos que era a geometria egípcia. Daí a denominação de Geometria Euclidiana, dada à parte da Geometria que estuda as figuras planas em geral. Ao longo dos séculos foram surgindo novas contribuições de várias origens, até chegarmos aos dias atuais. A Geometria é de grande valia na vida humana, especialmente no desenvolvimento de máquinas e equipamentos, edificações diversas, onde as formas derivam desses conhecimentos.

Conceitos primitivos ou que não se podem definir.

Há alguns conceitos primitivos que podemos apenas descrever, mas não definir ou materializar. Todos os demais conceitos derivam deles, uma vez que os usamos para definir os outros, mais complexos, mais elaborados.

Ponto – Se pegarmos um lápis, muito bem afinado e com ele tocarmos uma folha de papel ou outra superfície, a marca deixada nos dará a ideia de um ponto. Dizemos que nos dá a ideia de ponto, uma vez que este é infinitamente menor, o que equivale a dizer que o ponto não tem dimensão. Os pontos são identificados por meio de letras maiúsculas como A, B, C, D, ou P, Q, R, S e outras.

As marcas feitas na imagem acima, podem servir de uma localização de pontos, mas na realidade não são pontos, são conjuntos de pontos. São pequenas manchas.

Reta – se colocarmos justapostos um número infinito de pontos, sempre na mesma direção, teremos a representação de uma reta. Ela é infinita em ambos os sentidos. Sendo formada por pontos, ela não tem espessura. Um risco com o lápis ou caneta, nos dá uma representação da reta, mas apenas isso. Geralmente usamos uma letra minúscula para identificar uma reta. É comum usar para isso as letras como r, s, t, p, q ou qualquer uma das outras, dependendo das circunstâncias.

Por um ponto passam infinitas retas. Por dois pontos em um plano, é possível traçar uma e somente uma reta.

As infinitas retas que podemos traçar pelo ponto, abrangem todo espaço tridimensional.
Pelos pontos ${A}$ e ${B}$, podemos traçar somente a reta ${\overleftrightarrow{AB}}$, assim como pelos pontos ${C}$ e ${D}$, é possível traçar somente a reta ${\overleftrightarrow{CD}}$

Semi-retas: – um ponto sobre uma reta, divide a mesma em duas semi-retas, que têm como origem esse ponto e se prolongam até o infinito na mesma direções e em sentidos opostos. Uma semi-reta é representada pelo ponto de origem e outro ponto identificado, encimados por uma seta partindo da letra origem para a outra letra. Por exemplo ${\overrightarrow{PP’}}$ ou ${\overrightarrow{PP”}}$

Segmentos de reta: – denominamos segmento de reta a parte de uma reta compreendida entre dois pontos identificados sobre ela. Os segmentos de reta são identificados pelas letras associadas as extremidades, encimadas por um traço horizontal. Exemplo ${\overline{PQ}}$

Segmentos consecutivos: – segmentos consecutivos têm uma extremidade comum e fazem parte da mesma reta. Por fazerem parte da mesma reta também são denominados segmentos colineares. Na figura os segmentos ${\overline{PQ} ;\overline{QR}}$

Na primeira reta temos as semi-retas ${\overrightarrow{PP’} e \overrightarrow{PP”}}$. Na segunda reta podemos identificar o segmento de reta ${\overline{PQ}}$ e na terceira reta temos os segmentos consecutivos ${\overline{PQ} e \overline{QR}}$.

Plano: – se olharmos para uma folha de papel sobre uma mesa ou colocada na vertical, podemos imaginar o que é um plano se imaginarmos essa folha se estendendo infinitamente em todas as direções e sentidos imagináveis. O plano é infinito, mas não tem espessura. Um plano geralmente é identificado por uma letra grega, como ${\alpha}$; ${\beta}$; ${\gamma}$.

O plano se estende infinitamente em todas as direções imagináveis prolongando a folha ou a tela do computador.

Classificação de retas

Retas coplanares: – são retas que estão contidas no mesmo plano. Vejamos a figura a seguir.

As retas coplanares podem ser paralelas, convergentes ou ortogonais.

Retas de topo: – são retas que perfuram um ou mais planos em qualquer direção, como mostra a figura.

Dois planos ortogonais, são perfurados por retas em diferentes pontos e estas retas são denominadas retas de topo.

Retas paralelas: – são retas pertencentes a um mesmo plano e todos os seus pontos sucessivos são equidistantes. Em outras palavras elas se prolongam até o infinito, sem jamais se encontrarem, isto é, não têm nenhum ponto comum.

As retas r, s, t, u tem todos seus pontos pertencentes ao plano ${\alpha}$ e no entanto não têm nenhum ponto em comum entre elas.

Retas concorrentes: – são retas que podem pertencer a um mesmo plano e têm um ponto comum. Por um mesmo ponto podemos traçar infinitas retas.

As retas p, q e r pertencem ao mesmo plano ${\alpha}$. As retas p e q, concorrem no ponto C. As retas q e r concorrem no ponto B e as retas p e r convergem ou concorrem no ponto A. Cada uma dessas retas é concorrente de inúmeras retas que passam no mesmo ponto e em pontos diferentes.

Retas ortogonais: – são retas que formam entre elas um ângulo de 90º ou seja um ângulo reto. Elas determinam um plano, como é o caso $\beta$.

As retas x e y são concorrentes no ponto O e formam um ângulo reto, isto é, os quatro ângulos formados pelas semi-retas são todos iguais a 90º.

Retas oblíquas: – são retas coplanares que formam ângulos diferentes de 90º. Dois são iguais e menores que 90º e outros dois são iguais e maiores que 90º.

As retas r e s são concorrentes no ponto P e formam dois ângulos ${\theta \lt {90º}}$ e dois ângulos ${\alpha\gt{90º}}$.

Planos paralelos: – são planos cujos pontos determinados por retas ortogonais a eles e paralelas entre si, são sempre equidistantes. Veja ilustração da figura.

Duas retas paralelas perfuram os planos ${\alpha}$ e ${\beta}$, determinando dois segmentos congruentes (mesma medida) que são ${\overline{MN}}|$ e ${\overline{PQ}}$. Isso demonstra que os planos ${\alpha}$ e ${\beta}$ são paralelos.

Planos ortogonais: – são planos que se interceptam segundo uma linha reta e qualquer reta ortogonal a um deles, será obrigatoriamente paralela ao outro plano.

As retas r e s perfuram os planos $\alpha$ e $\beta$ num ângulo que mede $90º$ e são paralelas respectivamente aos dois planos ortogonais. Fica fácil observar que as mesmas retas são também ortogonais entre si.

Planos oblíquos: – são planos que se interceptam segundo uma linha reta, mas formam entre si ângulos $\neq{90º} $. Dois ângulos $\lt{90º}$ e dois angulos $\gt{90º}$.

Os planos oblíquos $\gamma$ e $\beta$ formam dois ângulos $\theta\lt{90º}$ e dois ângulos ${{180º – \theta}\gt{90º}}$.

Já vimos que existem linhas retas, que é o caso mais simples de linha. Agora vejamos os outros tipos de linhas possíveis.

Linhas curvas: – são formadas por um conjunto infinito de pontos, que não estão arrumados na mesma direção. A direção varia em cada ponto da linha.

Linha mista: – linha formada por porções curvas e porções retas, que podem se alternar.

Linha quebrada: – sequência de trechos retos e direções variadas.

Com estas informações teremos condições de desenvolver os próximos tópicos, que iniciaremos no post que virá em seguida.

Havendo dúvidas, não hesite em contactar-me por um dos canais abaixo listados, para esclarecimentos.

Curitiba, 23 de outubro de 2019

Décio Adams

[email protected]  

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhattsApp: (41) 99805-0732