Matemática – Aritmética. Curiosidade sobre divisibilidade por 11.

Curiosidade!

Não sei se é realmente uma curiosidade, ou se estou “redescobrindo” a roda. Mas estava eu às voltas com os critérios de divisibilidade, objeto de um artigo que publiquei em dias passados, quando me ocorreu verificar o caso dos números divisíveis por $\color{Navy}{11}$. Eu estava buscando um número de vários algarismos e que fosse divisível por $\color{Navy}{11}$. Lembrei que basta repetir um número, numa linha abaixo, deslocando o algarismo das unidades para as dezenas e assim até o final. Feito isso efetua-se a soma, resultando um número divisível. Vejamos como isso funciona para não deixar dúvidas.

Na figura está efetuada a multiplicação de $\color{Navy}{475\cdot 11} = \color{Red}{5225}$. No momento de fazer a multiplicação, vemos que multiplicamos o número duas vezes por ${1}$, apenas escrevendo os resultados com as colunas deslocados, uma vez que o segundo representa a multiplicação por $\color{Navy}{10}$ e poderíamos completar a coluna das unidades colocando ali um $\color{navy}{ 0}$. Um detalhe importante a ser notado, é que o último algarismo do produto é sempre igual ao último algarismo do número multiplicado por ${11}$.

A Prova Real da adição é feita subtraindo do total, uma das parcelas. Isso me levou a fazer o que segue. Peguei o número, nesse caso $\color{navy}{5225}$, escrevendo sob o algarismo das unidades o algarismo ${0}$ e subtraindo. Depois escrevi sob o algarismo das dezenas o resto da primeira subtração, ou seja o último algarismo. Efetuei a subtração e repeti o processo, até subtrair o último algarismo que deu ${0}$.

Note que, ao escrever o último resto, como próximo algarismo do subtraendo dessa operação, estava repetindo o resto, tendo o ${0}$ no final. Vejamos como isso terminou, colocando agora o ${7}$, até terminar.

Podemos notar que os mesmos algarismos do resto, estão na posição do subtraendo e o último algarismo da esquerda no resto deu ${0}$.

Pela regra vista nos critérios de divisibilidade em geral, faríamos a adição dos algarismos de ordem ímpar e os de ordem par, subtraindo um do outro. Se o resultado for divisível por ${11}$, o número analisado também é divisível. Vamos ver:

$\color{Navy}{S_{i} = 5 + 2 = 7}$
$\color{Navy}{S_{p} = 2 + 5 = 7}$
$\color{Navy}{S_{i} – S_{p} = 7 – 7 = 0}$
O número ${0}$ é divisível por qualquer número e portanto também por $11$. Logo o número ${5225}$ é divisível por ${11}$.
Vejamos outro exemplo para tirar as dúvidas.

Note que também aqui acontece a mesma coisa. Subtraindo o ${0}$ do último algarismo o resto é o próprio. Subtraindo esse algarismo do algarismo das dezenas, temos o segundo resto. Este subtraído do algarismo das centenas, nos dá o terceiro resto, que subtraído do algarismo dos milhares nos dá o último resto. Subtraímos este do algarismo das dezenas de milhares e teremos resto zero. Isso evidencia que o número ${80212}$ é divisível por${11}$. Para sanar a dúvida, apliquemos também aqui o critério da soma dos algarismos de ordem ímpar e ordem par:
${S_{i} = 8 + 2 + 2 = 12}$
${S_{p}= 0 + 1 = 1}$
${\Delta S=S_{i}- S_{p} = 12 – 1 = 11}$
Comprovamos que é divisível por ${11}$ e também validamos o critério apresentado no primeiro exemplo.

Vamos ver se isso funciona com outro número, que não seja divisível. Por exemplo $\color{Navy}{7439}$. Pelo critério geralmente usado teremos:
$\color{Navy}{S_{i} = 9 + 4 = 13}$
$\color{Navy}{S_{p}=3 + 7 = 10}$
$\color{Olive}{S_{i} – S_{p} = 13 – 10 = 3}$, que não é divisível por ${11}$, indicando que o número $\color{Navy}{7439}$ também não é.
Como fica aplicando o procedimento que eu observei.

Vemos que tudo foi igual ao outro exemplo, menos na última subtração, onde não foi possível fazer $\color{Navy}{6 – 9}$ e não tínhamos vizinho à esquerda para emprestar. Poderia ter ocorrido que a subtração fosse possível, mas desse diferente de ${0}$. Nesse caso, o número $\color{Navy}{7439}$ não é divisível por $\color{Navy}{11}$. Estou apresentando como uma “curiosidade”, para que mais pessoas testem o procedimento e opinem.Talvez até já seja do conhecimento de outras pessoas, mas não seja considerado algo digno de nota. Quem ler e testar, pode me dar sua opinião a respeito. Talvez seja possível desenvolver alguma discussão a respeito. Para colocar em teste, vamos observar mais alguns exemplos.

$\color{Brown}{{34793}\div {11} = ?}$
- Pelo critério geralmente usado
  - $\color{Olive}{S_{i} = 3 + 7 + 3 = 13}$
  - $\color{Olive}{S_{p} = 9 + 4 = 13}$
  - $\color{Navy}{S_{i} – S_{p} = 13 – 13 = 0}$ $\rightarrow$ é divisível por $11$.
- Pelo procedimento por mim apresentado.

A última subtração deu zero e por isso o número $ 34793$ é divisível por$ 11$, o que é confirmado pelo critério da soma dos algarismos de ordem ímpar e ordem par.

Podemos observar nitidamente que o resto e o subtraendo tem os mesmos algarismos, com a exceção do ${0}$, o que indica a multiplicação por ${10}$. Mas o último algarismo da esquerda agora foi igual a ${0}$, indicando divisibilidade por ${11}$. $\color{Olive}{{76549}\div {11} = ?}$

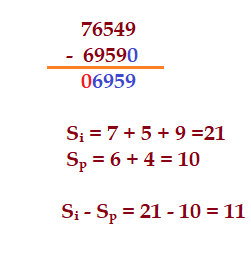
Os dois métodos confirmam o mesmo resultado. Número divisível por 11.

Abaixo do procedimento que identifiquei. O ${0}$ na última posição do resto, indica divisibilidade. Pelo critério geral. $\color{navy}{S_{i} =9 + 5 + 7 = 21}$ $\color{Navy}{S_{p} = 4 + 6 = 10}$ $\color{Navy}{S_{i} – S_{p} = 21-10 =11}$, isto também indica divisibilidade por $11$.

$\color{Olive}{{457963}\div{11} =?}$

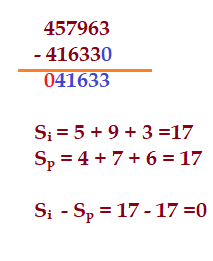
Abaixo está feita a demonstração pela subtração e o resultado indica que o número $\color{Olive}{457963}$ é divisível por $\color{olive}{11}$. Usando o critério comum.

$\color{Navy}{S_{i}=3+9+5 =17}$
$\color{Navy}{S_{p}=6+7+4=17}$
$\color{Olive}{S_{i}-S_{p}=17-17=0}$, indicando divisibilidade.

Podemos observar que nos casos em que o número é divisível, os dois critérios conferem no resultado. Vamos usar números não divisíveis para ver.

$\color{Olive}{{73259}\div{11} =?}$

Os dois critérios indicam que o número não é divisível por 11.

Pela subtração, notamos que não foi possível fazer a última subtração, pois não é possível fazer ${6 – 7}$, nessa forma. Não é divisível por ${11}$. Pela adição das ordens. $\color{Navy}{S_{i}=9+2+7=18}$ $\color{Navy}{S_{p}=5+3=8}$ $\color{Navy}{S_{i}-S_{p}=18-8=10}$, não é divisível por ${11}$.

$\color{Olive}{{827568}\div{11} =?}$

Os dois métodos indicam que o número fornecido não é divisível por 11.

O método da subtração mostra que não é divisível, pois o último algarismo da esquerda deu diferente de ${0}$. Pela adição das ordens.

$\color{Navy}{S_{i[}=8+5+2=15}$
$\color{Navy}{S_{p}=6+7+8=21}$
$\color{Olive}{S_{p}-S_{i}=21-15=6}$, não é divisível por ${11}$.

Os exemplos mostrados{ permitem deduzir que o procedimento é válido e, dependendo da prática, pode ser até mais rápido do que o outro. Vamos ver qual será a opinião dos meus leitores.

Treinar um pouco faz bem. Vamos verificar se os números a seguir são divisíveis por 11 ou não.

a) ${5724}$ ?

b) ${41294}$ ?

c)${7425}$ ?

d)${949007}$ ?

e)${4267}$?

f)${9339}$ ?

Obs.: Se você ler essa matéria, testar e julgar válida minha demonstração, me mande sua opinião. Se julgar inútil, ou sem validade, também me informe, para que possa ter uma ideia da aceitação ou não do procedimento.

Curitiba, 21 de julho de 2016. Revisado, melhorado e republicado em 05 de outubro de 2019.

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

5 de outubro de 201912 de junho de 2020

Matemática – Aritmética. Múltiplos e sub-múltiplos

Múltiplos e sub-múltiplos.

Já estudamos a multiplicação e sua inversa, a divisão.
A tábuada nos mostra o resultado da multiplicação dos números ${le10}$ entre si. O verbo multiplicar nos leva a palavra múltiplo. O resultado da multiplicação nos fornece um múltiplo do número multiplicado. Dessa forma podemos definir uma família de múltiplos para qualquer número. Por exemplo: ${f_{m}(3) =?}$. Essa família será um conjunto de todos os múltiplos do número ${3}$ (tres). Começaremos multiplicando por ${\{0,1,2,3,4,5…\}}$ e assim sucessivamente. Logo essa família é infinita.
$\color{navy}{f_{m}(3) = \{0, 3, 6, 9, 12, 15, 18, …\}}$
$\color{navy}{f_{m}(5) =\{0, 5, 10, 15, 20, 25, 30, …\}}$
Percebemos imediatamente que todas as famílias de múltiplos começam com o número 0 (zero), pois todos serão multiplicados por ele e o resultado só pode ser esse. A multiplicação de cada número por ${1}$ (um), dá o próprio número e assim sucessivamente.
Podemos escrever de modo genérico \[\bbox[5px,border: 2px solid olive]{\color{brown}{f_{m}(n) = \{0\cdot n, 1\cdot n, 2\cdot n, 3\cdot n, …\}}}\]

Continue lendo

5 de outubro de 20195 de outubro de 2019

Matemática – Aritmética. Números primos

Números primos
Oigalê! Números também tem primos e primas, que nem a gente?

Na verdade é a denominação dada a um grupo de números com uma característica bem definida. Se verificarmos sua família de divisores, veremos que ela tem somente dois elementos. O número ${1}$ (um) e o próprio número. São números que não são divisíveis por outros números, além da unidade e de si próprios. Vejamos.

$\color{navy}{ fd(1) = \{1\}}$ $\rightarrow$, é primo.
$\color{navy}{ fd(2) = \{1, 2\}}$ $\rightarrow$, é primo.
$\color{navy}{ fd(3) = \{1,3\}}$ $\rightarrow$, é primo.
$\color{navy}{ fd(4) = \{1,2,4\}}$ $\rightarrow$, não é primo. Tem um terceiro divisor.
$\color{navy}{ fd(5) = \{1,5\}}$ $\rightarrow$, é primo.
$\color{navy}{ fd(6) = \{1,2,3,6\}}$ $\rightarrow$, não é primo. Tem vários divisores
$\color{navy}{ fd(7) = \{1,7\}}$ $\rightarrow$, é primo.
$\color{navy}{ fd(8) = \{1,2,4,8\}}$ $\rightarrow$, não é primo. Tem vários divisores.
$\color{navy}{ fd(9) = \{1,3,9\}}$ $\rightarrow$, não é primo. Tem um terceiro divisor
$\color{navy}{ fd(10)= \{1,2,5,10\}}$ $\rightarrow$, não é primo. Divisores diversos.
$\color{navy}{ fd(11)= \{1,11\}}$ $\rightarrow$, é primo.
$\color{navy}{ fd(12)= \{1, 2, 3, 4, 6, 12\}}$ $\rightarrow$, não é primo.
$\color{navy}{ fd(13)= \{1,13\}}$ $\rightarrow$, é primo.
Notamos que aos poucos os números primos vão ficando mais esparsos no meio dos números divisíveis por outros números. Para saber se um número é primo ou não, existem meios de fazer isso. Quando se trata de um número de valor mais elevado, demoraríamos algum tempo, tentando escrever todos os seus divisores. E daí entramos com um outro recurso.

Continue lendo

4 de outubro de 201913 de junho de 2020

Matemática – Aritmética. Divisibilidade, aplicação dos critérios.

Divisibilidade.

Recordando os critérios de divisibilidade, vamos resolver alguns exercícios sobre o assunto, antes de continuarmos com os outros casos.

Verifique a divisibilidade dos números a seguir.
- $\color{Navy}{1546}$
- O último algarismo é par e portanto é divisível por 2 (dois). $\color{Navy}{1546\div 2= 773}$
- A soma dos algarismos $\color{Navy}{S=1+5+4+6= 16}$. Esse número não é divisível por $\color{Navy}{3}$ e portanto o primitivo também não é.
- termina em $\color{Navy}{6}$ e assim não é divisível por $\color{Navy}{5}$.
- O dobro do último algarismo é $\color{Navy}{2\cdot 6 = 12}$. Subtraindo esse valor do número formado pelos algarismos restantes, temos $\color{Navy}{154 – 12 = 142}$. O número obtido não é divisível por $\color{Navy}{7}$.
- A soma das ordens pares e ímpares $\color{Navy}{S_{i} = 6 + 5 = 11}$ e $\color{Navy}{S_{p}= 4 + 1 = 5}$. A diferença entre essas somas $\color{Navy}{S_{i} – S_{p} = 11 – 5 = 6}$. Como o resultado não é múltiplo de $\color{Navy}{11}$, o número também não é divisível por $\color{Navy}{11}$.

Continue lendo

4 de outubro de 20194 de outubro de 2019

Matemática – Aritmética. Valores absolutos e relativos dos algarismos

Sistema de numeração decimal.

Durante séculos, mais provavelmente milênios, o homem usou vários sistemas para contar suas coisas. As pesquisas arqueológicas e mesmo documentos escritos em diferentes meios e formas, nos trazem notícias de sistemas de numeração com diferentes bases. Provavelmente isso já era uma evolução em relação a uma forma mais rudimentar, onde se tentaria associar um símbolo a cada quantidade, tornando o sistema de qualquer cálculo algo simplesmente impossível.

Quando percebeu que era possível usar uma quantidade limitada de símbolos para escrever números de valores elevados, sem o menor problema, o homem adotou alguns sistemas. Os sumérios e mais tarde os babilônios seguidos pelos assírios, adotaram um sistema de numeração sexagesimal, do qual herdamos a contagem do tempo em horas, minutos e segundos. Os ângulos em graus, minutos e segundos.

Continue lendo

3 de outubro de 201931 de maio de 2020

Matemática – Aritmética. Divisão exata e aproximada de números.

Divisão decimal aproximada.

Quando estudamos a divisão, vimos que grande parte das vezes essa operação não é exata, sobrando ao final do processo, um resto menor que o divisor. Naquele momento deixamos de efetuar esse complemento da operação. Ficamos com o resultado:

$\color{navy}{quociente\cdot divisor + resto = dividendo}$

Agora, vamos determinar o resultado da operação, com uma aproximação na forma de número decimal. Para isso recorremos à colocação de uma vírgula após o último algarismo inteiro obtido no quociente e acrescentamos um zero no resto. A partir daí tentamos continuar a divisão. Se ainda não for possível, acrescentamos um zero ao quociente e mais outro no resto. Podemos continuar assim indefinidamente. Talvez em algum momento ocorra uma divisão exata, ou então teremos uma dízima periódica, quando um ou mais algarismos começam a se repetir no quociente. O melhor de tudo é fazer isso na prática.

Continue lendo

3 de outubro de 201916 de maio de 2020

Matemática – Aritmética

Multiplicar números com vírgulas.

Ao multiplicarmos números contendo vírgula, é quase certo de que o produto também conterá vírgula. Como iremos proceder para fazer essas multiplicações com segurança e sem errar?
Iremos colocar os números como se fossem inteiros e realizar a multiplicação da mesma forma. Feita a operação, iremos contar o número de algarismos existentes após a vírgula, tanto no multiplicando quanto no multiplicador e, contando esse número da direita para esquerda no produto, colocaremos a vírgula.

Continue lendo

2 de outubro de 201916 de maio de 2020

Matemática – Aritmética

Multiplicação de números por dez, seus múltiplos e sub-múltiplos

Vamos multiplicar os decimais por 10!

Anteriormente falamos na multiplicação de números inteiros por ${10}$ e seus múltiplos. Agora que já conhecemos os números com aproximação decimal após a vírgula, vamos ver como ficam eles, quando multiplicados por ${10, 100, 1000 ou 0,1; 0,01; 0,001}$ e assim por diante.

Vamos lembrar, onde foi que colocamos a vírgula, quando fizemos as divisões não exatas. Não foi depois dos algarismos ditos inteiros? Pois é isso mesmo. De forma que um número inteiro, tem, depois de seu último algarismo uma vírgula, que fica subentendida, uma vez que não há parte decimal. Vamos ver o que acontece com a vírgula, nessa multiplicação.

Continue lendo

1 de outubro de 201914 de junho de 2020

Matemática – Aritmética – Notação exponencial ou científica

Epa! Que bicho é esse?

A matemática é aplicada em todos os campos da atividade humana. Não raro temos a necessidade de escrever números extremamente pequenos e outras tantas vezes nos deparamos com outros números imensamente grandes. Tanto em uma situação, quanto em outra, acabamos ficando com dificuldades de exprimir ou mesmo fazer a leitura correta desses números extremos.

Continue lendo

27 de setembro de 201916 de maio de 2020

13.4.1 – Matemática – Aritimética operações com radicais.

Vamos trabalhar mais um pouco com radicais?

Efetue as operações indicadas entre radicais.

a) ${\frac{{\sqrt[3]{2401}}\cdot{(2)}\cdot{\sqrt[3]{7}}}{\sqrt{343}}}$

Fatorando os radicandos e exprimindo na forma exponencial

${\frac{{\sqrt[3]{7^{4}}}\cdot{(2)}\cdot{\sqrt[3]{7}}}{\sqrt{7^{3}}}}$

Simplificando os radicais

${\frac{{\sqrt[3]{7^{3}\cdot {7}}}\cdot{(2)}\cdot{\sqrt[3]{7}}}{\sqrt{7^{2}\cdot{7}}}}$

${\frac{{{7}\cdot\sqrt[3]{7}}\cdot{(2)}\cdot{\sqrt[3]{7}}}{{7}\cdot\sqrt{7}}}$

${\frac{{{14}\cdot{\sqrt[3]{7}}}}{{7}\cdot\sqrt{7}}}$

${\frac{{{2}\cdot{\sqrt[3]{7}}}}{\sqrt{7}}}$

Reduzindo ao mesmo índice: m.m.c (2 e 3) = 6

${\frac{{{2}\cdot\sqrt[6]{7^{2}}}}{\sqrt[6]{7^{3}}}}$

${{2}\cdot\sqrt[6]{\frac{7^{2}}{7^{3}}}}$

${{2}\cdot\sqrt[6]{7^{2 – 3}}}$

${{2}\cdot\sqrt[6]{7^{-1}}}$

b) ${\left[\frac{\left({\sqrt[5]{2048}} : {\sqrt[5]{15625}}\right)\cdot{\sqrt[3]{5^{4}}}}{{3}\cdot\sqrt[3]{5^{2}}}\right]}$

Exprimindo os radicandos na forma de potências por fatoração:

${\left[\frac{\left({\sqrt[5]{2^{11}}}\right) : \left({\sqrt[5]{5^{6}}}\right)\cdot{\sqrt[3]{5^{4}}}}{{3}\cdot\sqrt[3]{5^{2}}}\right]}$

${\left[\frac{\left({\sqrt[5]{2^{10}\cdot{2}}}\right) : \left( {\sqrt[5]{5^{5}\cdot{5}}}\right)\cdot{\sqrt[3]{5^{3}\cdot{5}}}}{{3}\cdot\sqrt[3]{5^{2}}}\right]}$

${\left[\frac{\left({{4}\cdot\sqrt[5]{2}}\over{{5}\cdot\sqrt[5]{5}}\right)\cdot{{5}\cdot\sqrt[3]{5}}}{{3}\cdot\sqrt[3]{5^{2}}}\right]}$

Reduzindo os radicais ao mesmo índice: mmc(3; 5) = 15 e simplificando os fatores comuns.

${\left[\frac{\left({{4}\cdot\sqrt[15]{2^{3}}}\over{{5}\cdot\sqrt[15]{5^{3}}}\right)\cdot{{5}\cdot\sqrt[15]{5^{5}}}}{{3}\cdot\sqrt[15]{5^{10}}}\right]}$

${\left[\frac{\left({{4}\cdot\sqrt[15]{2^{3}}}\over{\sqrt[15]{5^{3}}}\right)\cdot{\sqrt[15]{5^{5}}}}{{3}\cdot\sqrt[15]{5^{10}}}\right]}$

${\left({4\sqrt[15]{{2^{3}}{5^{5}}}}\over\sqrt[15]{5^{3}}\right)}\cdot{\left({1}\over{3}\sqrt[15]{5^{10}}\right)}$

${{4\sqrt[15]{{2^{3}}{5^{5}}}}\over{{3}\sqrt[15]{{5^{3}}\cdot{5^{10}}}}}$

${\left({4}\over{3}\right)\cdot\sqrt[15]{{2^{3}}\over{5^{8}}}}$

c) ${\left({{a^2}\sqrt[3]{{b^5}\cdot{c^4}}}\over{{b^3}\sqrt[3]{{a^4}\cdot{c^5}}}\right)}$

Introduzindo os fatores externos nos radicais teremos:

${\left({\sqrt[3]{{a^6}\cdot{b^5}\cdot{c^4}}}\over{\sqrt[3]{{a^4}\cdot{b^6}\cdot{c^5}}}\right)}$

Simplificando os fatores comuns sobra:

${\left({\sqrt[3]{{a^2}\over{b}\cdot{c}}}\right)}$

d) ${\left[{\left({3{x}\sqrt[3]{x^2 + y}}\right)\cdot\left({2{y}\sqrt{x^2 – y}}\right)}\over{{9}\sqrt[3]{x^4 – y^2}}\right]}$

Cancelando os fatores comuns, fica:

${\left[{\left({{x}\sqrt[3]{x^2 + y}}\right)\cdot\left({2{y}\sqrt{x^2 – y}}\right)}\over{{3}\sqrt[3]{x^4 – y^2}}\right]}$

Introduzindo os fatores externos nos radicais:

${\left[{\left({\sqrt[3] {{x^{3}}\cdot{(x^2 + y)}}}\right)\cdot\left(\sqrt[2]{{2^{2}{y^{2}}\cdot {(x^2 – y)}}}\right)}\over{\sqrt[3] {{3^{3}} {(x^4 – y^2)}}}\right]}$

Reduzindo os radicais ao mesmo índice: mmc(2;3) = 6

${\left[{\left({\sqrt[6] {{x^{6}}\cdot{(x^2 + y)^{2}}}}\right)\cdot\left(\sqrt[6]{{2^{6}{y^{6}}\cdot {(x^2 – y)^{3}}}}\right)}\over{\sqrt[3] {{3^{3}} {(x^4 – y^2)}}}\right]}$

${\sqrt[6]{{{2^{6}\cdot{x^{6}}\cdot{y^{6}}\cdot{(x^{2} +y)}^{2}\cdot{(x^{2} – y)}^{3}}}\over{{3^{6}} {(x^4 – y^2)}^{2}}}}$

${{{2xy}\over{3}}\sqrt[6]{{{(x^{2} +y)}^{2}\cdot{(x^{2} – y)}^{3}}\over{{(x^2 + y)^{2}(x^2 -y)^{2}}}}}$

${{{2xy}\over{3}}\sqrt[6]{x^{2} – y}}$

Agora é sua vez

Efetue as operações com os radicais e simplifique o que for possível.

a) ${\sqrt[3]{4096}\cdot\sqrt[5]{(x + y)}^{10}}$

b)${{{2x}\sqrt[2]{(a^{2} + b)^{3}}\cdot\sqrt[3]{(a^{2} + b)^{2}}}\over\sqrt[3]{(a^{4} – b^{2})}}$

c) ${{\sqrt[3]{(4x^{2} – 12x + 9)}\cdot\sqrt[2]{(x^{2} – 1)}}\over\sqrt[2]{(x + 3)\cdot(x + 1)}}$

d)${{{5x^{2}}\sqrt[3]{(x + y^{2})^{6}}}\over{{6y}\sqrt[2]{(x^{2} – y^{4}}}}$

e)${{{(2x – y)}\cdot\sqrt[3]{2x + y}}\over{\sqrt[2]{(4x^{2} – y^{2})}}}$

f) ${{{3a}\sqrt[2]{2a}} + {{5b}\sqrt[6]{8a^3}} – {{2b}\sqrt[4]{4a^2}}}$

g)${\left[{\sqrt[6]{(x^2 – 1)}^2}\cdot{\sqrt[3]{(x^2 + 1)}^2}\right]\cdot{2y}\sqrt[2]{x^2 – 1}}$

h)${\left[{{\sqrt{(2a + b)}^3}\cdot{\sqrt[5]{(2a + b)}^2}}\over{{3ab}\sqrt[5]{(2a – b)\cdot(4a^2 – b^2)}}\right]}$

Se tiver dificuldades na solução dos exercícios propostos, entre em contato por meio de um dos canais abaixo listados e resolveremos as dificuldades.

Curitiba, 27 de setembro de 2019.

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732