Estudo detalhado do triângulo equilátero.
Depois de termos visto o Teorema de Pitágoras, podemos aplicar esse conhecimento na determinação de elementos notáveis dos triângulos equiláteros.
Como foi visto acima, é o único triângulo classificado como figura geométrica regular. Isso implica em que o traçado de suas alturas, bissetrizes dos ângulos, medianas e mediatrizes sejam coincidentes, interceptando-se em um mesmo ponto que é o centro geométrico do triângulo ou seja é o baricentro, ortocentro, incentro e circuncentro. Iremos estabelecer modos de determinação das medidas da altura, do apótema e do raio da circunferência circunscrita.
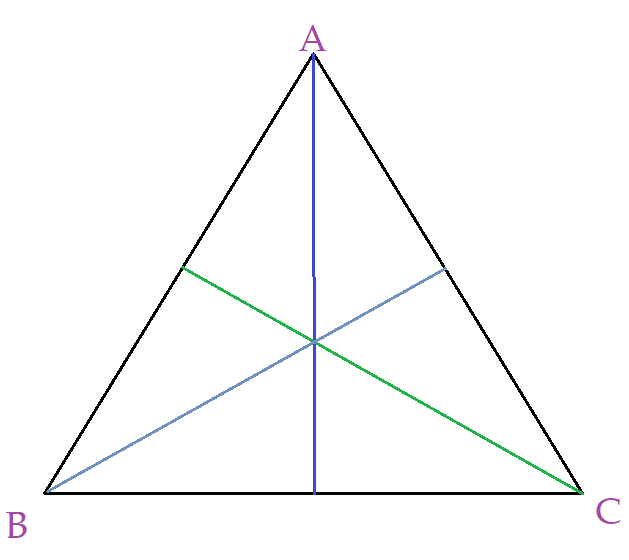
O ponto $M$, divide o lado $\overline{BC}$ em dois segmentos congruentes, equivalentes à metade do lado do triângulo. Portanto $\overline{MC} = {{l}\over{2}}$, determinando assim um triângulo retângulo $\Delta{(AMCA)}$, onde podemos aplicar o Teorema de Pitágoras.
$\overline{AC} = l $ $\Rightarrow$ hipotenusa.
$\overline{AM} = h $ $\Rightarrow$ altura do triângulo e é um dos catetos.
$\overline{MC} = {{l}\over{2}}$ $\Rightarrow$ cateto.
${l}² = h² + ({{l}\over {2}})²$ $\Leftrightarrow$ $h² = l² – {{l²}\over{4}}$
$\sqrt{h²} = {{{{4}\cdot{l²}} – l²}\over{4}}$
$h = {{{3}\cdot{l²}}\over{4}}$ $\Leftrightarrow$ $h = \sqrt {{{3}\cdot{l²}}\over{4}} $
$h = {{{l}\cdot\sqrt{3}}\over{2}}$
O apótema equivale ao segmento que representa o raio da circunferência inscrita no interior do retângulo equilátero.
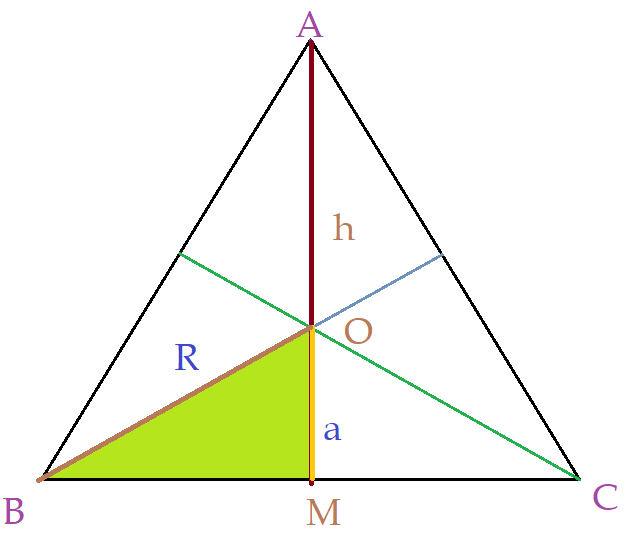
No triângulo destacado, temos:
$\overline{BO}$ $\Rightarrow$ raio da circunferência circunscrita (hipotenusa). Equivale à diferença entre a altura e o apótema.
$R = h – a $
$\overline{BM} ={{l}\over{2}}$ $\Rightarrow$ cateto.
$a$ $\Rightarrow$ apótema que é igual ao raio da circunferência inscrita.
$R² = a² + ({{l}\over{2}})²$ $\Leftrightarrow$ ${h – a}² = a² + {{l²}\over{4}}$
${h² – 2ah + a²} = a² + {{l²}\over{4}}$ $\Leftrightarrow$ $h² – 2ah =a² – a² +{{l²}\over{4}}$
$h² – {{l²}\over{4}} = 2ah$ $\Leftrightarrow$ $a = {{h^2 – {{l^2}\over{4}}}\over{2h}}$
$a = {{\left({{l}\sqrt{3}\over{2}}\right)^2 -{l²}}\over{{2{l}\sqrt{3}}\over{2}}}$$\Leftrightarrow$$a = {{{3{l}² – {l}²}\over{4}}\over{l\sqrt{3}}}$
$a = {{2{l}²\over{4}}\over{l\sqrt{3}}}$ $\Leftrightarrow$ $a = {{l²}\over{2}}\cdot{{1}\over{l\sqrt{3}}}\cdot{\sqrt{3}\over\sqrt{3}}$
$a = {{l\sqrt{3}}\over{6}}$
Estabelecemos acima que ${R = h – a}$ de onde podemos deduzir a expressão de $R$ em função do lado do triângulo.
$R = {{l}\sqrt{3}\over{2}} – {{l}\sqrt{3}\over{6}}$
$R = {{{3\cdot{{l}\sqrt{3}}} – {{l}\sqrt{3}}}\over{6}}$
$R = {{2{l}\sqrt{3}}\over{6}}$
$R = {{l}\sqrt{3}\over{3}}$
Comparando esses três elementos, podemos estabelecer que:
${{{h}\over{a}} = {{{l}\sqrt{3}\over{2}}\over{{l}{\sqrt{3}}\over{6}}}}$ $\Leftrightarrow$ ${{{h}\over{a}} = {{{l}\sqrt{3}\over{2}}\cdot {{6}\over{{l}\sqrt{3}}}}}$
${h\over {a}} = {\not{6}\over\not{2}}$ $\Leftrightarrow$ $ a = {1\over3}\cdot h $
${{{h}\over{R}} = {{{{l}\sqrt{3}}\over{2}}\over{{{l}\sqrt{3}}\over{3}}}}$$\Leftrightarrow$${{{h}\over{R}} = {{{{l}\sqrt{3}}\over{2}}\cdot{{3}\over{l}\sqrt{3}}}}$
${{h}\over{R}} = {3\over2}$
$R = {2\over3}\cdot h$
${{a}\over{R}} = {{{{l}\sqrt{3}}\over{6}}\over{{{l}\sqrt{3}}\over{3}}}$$\Leftrightarrow$$ {{a}\over{R}} = {{{{l}\sqrt{3}}\over{6}}\cdot{{3}\over{{l}\sqrt{3}}}}$
$a = {1\over2}\cdot R$
Vejamos as circunferências inscrita e circunscrita num triângulo equilátero.
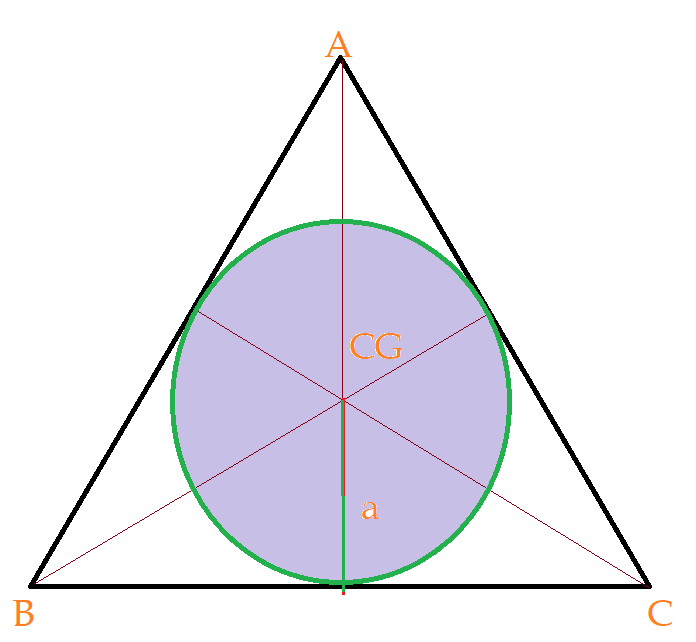
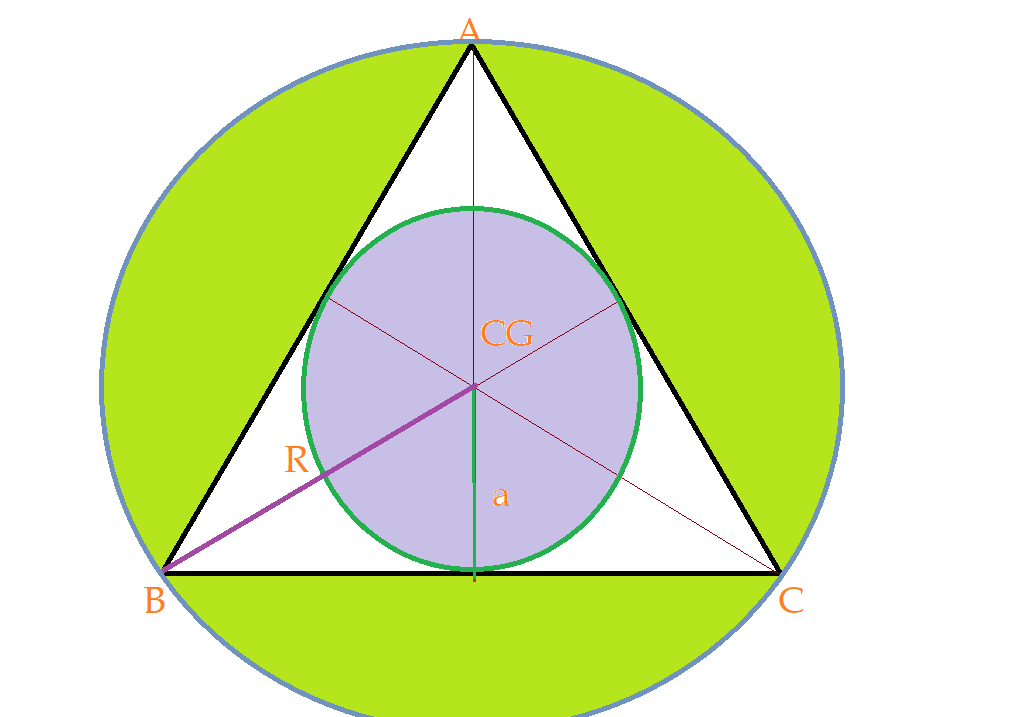
Perímetro
Denominamos perímetro a soma das medidas de todos os lados de um polígono. Se imaginarmos fazer uma cerca ao redor do polígono usando arame, qual seria o comprimento de um fio desse produto para dar uma volta completa? Com certeza todos dirão que é só somar os lados. Pronta a resposta. Por isso dizemos que:
Perímetro de um triângulo equilátero é a soma de seus três lados.
$ p = l + l + l$ $\Leftrightarrow$$ p = 3\cdot l$
Vamos exercitar um bocado.
- Um triângulo equilátero tem uma circunferência inscrita, cujo raio mede $7,0 cm$. Pede-se determinar o raio da circunferência circunscrita, a altura do triângulo e a medida do lado. Calcule também a área do triângulo.
$ r = a = {1\over2}\cdot{R}$ $\Leftrightarrow$$ 7 = {R\over2}$
$R = {7,0}\cdot{2} = 14,0 cm$
$h = a + R$
$h = 7,0 + 14,0 = 21,0 cm$
$h = {{{l}\sqrt{3}}\over{2}}$
$21,0 = {{{l}\sqrt{3}}\over{2}}$$\Leftrightarrow$${(21,0)}\cdot{2} = {l}\sqrt{3}$
${{(42,0)}\over\sqrt{3}} = l $ $\Leftrightarrow$${{{(42,0)}\cdot\sqrt{3}}\over\sqrt{3}} = l$
$l = {{{(42,0)}\cdot\sqrt{3}}\over{3}} = {{(14,0)}\cdot\sqrt{3}} cm$
$S_{3} = {{b\cdot h}\over2}$
$b = l = {(14,0)\cdot\sqrt{3}}$
$h = 21.0 cm$
$S_{3}= {{{(14,0)\cdot\sqrt{3}}\cdot{(21,0)}}\over2}$
$S_{3} = {(147,0)}\sqrt{3} cm$
2. Uma circunferência de raio $R = 30,0 cm$ é circunscrita a um triângulo equilátero. Pede-se determinar o raio da circunferência inscrita, a altura e o lado do triângulo, além de sua área.
$R = 30,0 cm$
$a = {R\over2}$
$a ={{(30,0)}\over{2}} = 15,0 cm$
$r = a = 15,0 cm$
$h = R + a$ $\Leftrightarrow$ $ h = 30,0 + 15,0 = 45,0 cm$
$h = {{{l}\cdot\sqrt{3}}\over{2}}$
$(45,0) = {{{l}\sqrt{3}}\over{2}}$$\Leftrightarrow$${{{(45,0)}\cdot{2}}\over\sqrt{3}} = l$
${{{(90,0)}\sqrt{3}}\over\sqrt{3}} = i$$\Leftrightarrow$$ l = {{(90,0)\sqrt{3}}\over{3}}$$\Leftrightarrow$$l = (30,0)\sqrt{3} cm$
$S_{3}= {{b\cdot h}\over2}$
$S_{3}= {{(30,0)\sqrt{3}\cdot (45,0)}\over2}$
$S_{3}= {(15,0)\cdot(45,0)\sqrt{3}}$$\Leftrightarrow$ $S_{3}= (675,0)\sqrt{3} cm²$
3. Um triângulo equilátero tem o lado medindo $ l = 27,0 m$. Pede-se determinar o raio da circunferência circunscrita, o raio da circunferência inscrita, a altura e a área da figura.
$R = {{l\sqrt{3}}\over 3}$
Sendo $ l = 27,0 m$, ficamos com:
$R = {{(27,0)\sqrt{3}}\over{3}}$$\Leftrightarrow$$R = (9,0)\sqrt{3} m$
$r = a = {{l\sqrt{3}}\over6}$
$r = {{(27,0)\sqrt{3}}\over 6}$$\Leftrightarrow$$ r = {{(9,0)\sqrt{3}}\over 2} m$
$h = {{l\sqrt{3}}\over 2}$
$h = {{(27,0)\sqrt{3}}\over 2}$$\Leftrightarrow$$ h = (13,5)\sqrt{3} m$
$S_{3}= {{b\cdot h}\over2}$
$S_{3} = {{(27,0)\cdot(13,5)\sqrt{3}}\over 2}$
$S_{3} = 182,25\sqrt{3} m²$
4. Um proprietário de terras, deseja cercar uma área em forma de triângulo equilátero, com 5(cinco) fios de arame liso. Se um dos lados da área mede $l = 200,0 m$, quantos metros de fio ele irá gastar para completar a cerca?
Se $p = 3\cdot l$$\Leftrightarrow$$ p = 3\cdot{200,0} = 600,0 m$
Cada fio de arame consumirá $600,0 m$ do material. Se ele quer colocar 5(cinco) fios, irá gastar:
$P = 5\cdot p$ $\Leftrightarrow$$ P = 5\cdot{600,0} = 3000,0 m$
Chegou a sua vez. Mostre do que é capaz.
- Se um círculo de raio $r = 12,0 cm$ está inscrito em um triângulo equilátero, determine: a) o raio do círculo circunscrito; b) a altura do triângulo; c) o lado do triângulo; d) a área do triângulo.
- Um triângulo equilátero está inscrito em uma circunferência de raio $R = 25,0 cm$. Calcule o raio do círculo inscrito nesse triângulo, a altura do triângulo e o seu lado.
- Um triângulo equilátero tem altura de $h = 18,0 cm$. Quer-se saber quanto mede o raio da circunferência inscrita, o lado do triângulo e a sua área. É possível circunscrever um círculo perfeito a esse triângulo? Se for, qual é seu raio.
- O perímetro de um triângulo equilátero (soma dos lados) é $p = 54,0 cm$. Determine sua altura, o apótema, o raio da circunferência circunscrita e a área do triângulo.
- Um triângulo equilátero, justapõe-se a outro igual a ele, formando um losango. Sendo as diagonais desse losango de medidas $d = 12,0 cm$ e $D ={(8,0)\sqrt{3}}cm$, determine sua área, a medida dos lados, o raio da circunferência inscrita e o raio da circunferência circunscrita aos vértices mais distantes.
- Um homem possui no terreno de sua casa uma sobra onde pretende colocar cerca murada. A forma é de um triângulo equilátero e vai precisar de 24 unidades de tijolos de 25,0cm, para cada fileira de um lado. Se quer fazer o muro com 8 (oito) fileiras de tijolos, quantos tijolos irá precisar para completar a obra?
- Dois irmãos são sócios em 50% para cada um de um terreno em forma de triângulo equilátero. Eles querem construir suas casas e para isso precisam demarcar as parcelas que cabem a cada um. Visando proteger o terreno de intrusos, quando ali forem colocar o material para a construção, querem construir muros de todos os lados e também na divisória. Se o lado do terreno mede $l = 50,0 m$, quantos metros de muros terão que construir? Se o código de edificações em área residencial da prefeitura permite ocupar 40% da área, qual é a área máxima que cada um deles poderá ocupar com a sua moradia?
- A diagonal menor de um losango, divide a figura em dois triângulos equiláteros. Se $d = 15,0 m$, determine a área de cada triângulo e a área do losango. Determine a diagonal maior da figura resultante. Determine o raio da circunferência que poderá ser inscrita na figura completa.
No caso de haver dificuldades, não hesite. Peça ajuda por meio de qualquer um dos canais abaixo.
Curitiba, 30 de outubro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

