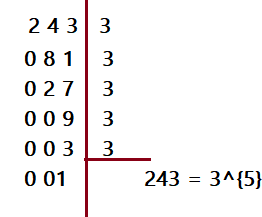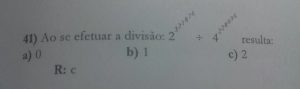Divisão – Propriedades
A divisão, de modo semelhante à multiplicação, da qual é a operação inversa, poderia ser representada como uma subtração sucessiva de termos. Por exemplo:
- $\color{navy}{30 : 6 = 5}$
- $\color{navy}{30 – 6 – 6 – 6 – 6 – 6 = 0}$
Subtraímos do dividendo $\color{navy}{30}$(trinta) cinco vezes o divisor $\color{navy}{6}$ e sobrou $0$(zero). Isso por ser uma divisão exata. O número de subtrações sucessivas é igual ao quociente. Se a divisão não for exata, iremos ter no final um resto menor que o divisor. Vejamos.
- $\color{navy}{47 : 7 = 6}$, sobrando resto $\color{navy}{5}$.
- $\color{navy}{47 – 7 – 7 – 7 – 7 – 7 – 7 = 5}$ $\Leftrightarrow$ $\color{navy}{(7 + 7 + 7 + 7 + 7 + 7 + 5 = 47})$
Subtraímos seis vezes o divisor $\color{navy}{7}$ do dividendo $\color{navy}{47}$ e na última subtração, ficou sobrando o resto $\color{navy}{5}$. Para obter novamente o dividendo, somamos seis parcelas iguais a $\color{navy}{7}$ e no final também o resto $\color{navy}{5}$.
Podemos facilmente deduzir que a divisão não goza de todas as propriedades da multiplicação, assim como a subtração não goza das propriedades da adição. O que foi dito acima, vale para as divisões exatas, como vimos. Se sobrar resto, não obtemos um resultado inteiro. Esse assunto será estudado ao abordar o conjunto dos números racionais (fracionários).
- Propriedade distributiva: Vejamos a seguinte situação.
- $\color{navy}{(15 + 18)\div 3 = 33\div 3 = 11}$
- $\color{navy}{(15\div 3) + (18\div 3) = 5 + 6 = 11}$
- Neste caso, fizemos uma distribuição do divisor pelos termos da adição que forma o dividendo.
- $\color{navy}{ (55 – 33)\div 11 = 22\div 11 = 2}$
- $\color{navy}{(55\div 11) – (33\div 11) = 5 – 3 = 2}$
- Fizemos o mesmo com a subtração e podemos dizer que o divisor é distributivo em relação aos termos da soma ou subtração.
- Se colocarmos na ordem inversa, como por exemplo $\color{navy}{64\div (12 + 4) = 64\div 16 = 4}$. Não podemos fazer a distribuição do dividendo pelos dois termos do divisor. $\color{navy}{(64\div 12) + (64\div 4) = \frac{64}{12} + 16 \not= 4}$.
- Isso nos mostra que a propriedade distributiva na divisão, se aplica ao divisor que pode dividir os termos da adição ou subtração, sem alterar o resultado. Já com o dividendo não acontece o mesmo. Por isso não posso afirmar que a divisão goza da propriedade distributiva em relação à adição e subtração, como acontece na multiplicação.
- Elemento neutro – outro dia uma leitora dessa matéria me perguntou por que eu considerei que a divisão não goza do elemento neutro e afirmou que ela o considerava como sendo o número $1$. Analisei e foi preciso dar razão a ela, mas fazendo a ressalva, como aliás já fiz também para a multiplicação, de que isso só vale com o número natural $1$, quando ele é o divisor. O que só vem confirmar a afirmação de que esta propriedade não se aplica na divisão.
Resumo das propriedades:
Adição:
- Comutativa – a ordem das parcelas não altera a soma.
- Associativa – podemos substituir duas ou mais parcelas pela sua soma (associação), sem alterar a soma final.
- Elemento Neutro – adicionar uma parcela igual a zero a uma soma, não altera o resultado. Zero é o Elemento neutro da adição.
- Propriedade do fechamento – a adição sempre é possível no conjunto dos números naturais. A soma de dois números naturais, é igual a outro número natural.
Multiplicação:
- Comutativa – a ordem dos fatores não altera o produto.
- Associativa – podemos substituir dois ou mais fatores pelo seu produto (associação), sem alterar o produto final.
- Elemento Neutro – multiplicar por 1(hum) não altera o produto. O número 1(hum) é o elemento neutro da multiplicação.
- Distributiva em relação a adição e subtração – a multiplicação de um fator por uma soma ou subtração, pode ser feita distribuindo o fator por cada um dos termos e depois realizar a adição ou subtração entre os resultados. O produto final será o mesmo.
- Fechamento: Vimos que a multiplicação de dois números naturais é sempre possível, ou seja, um número natural multiplicado por outro, resulta num produto que é um número natural.
Subtração: Não goza das propriedades comutativa, associativa,elemento neutro e fechamento no conjunto dos números naturais.
Divisão: Não goza das propriedades comutativa, associativa. O elemento neutro é o número natural $1$ quando colocado como divisor, jamais como dividendo. Isso equivale a dizer que a propriedade não se aplica. A propriedade distributiva em relação a adição e subtração, funciona apenas com o divisor. Com o dividendo não funciona. Na prática não devemos usar essa propriedade para a divisão.
Curitiba, 19 de outubro de 2018
Décio Adams
[email protected]
[email protected]
[email protected]
www.facebook.com/livros.decioadams
www.facebook.com/decio.adams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celulares: (41) 99805-0732