Linhas Poligonais
Linhas poligonais abertas são as linhas em que as extremidades não se tocam. Podem ser curvas, segmentos de reta, um tendo extremidade comum com o seguinte.
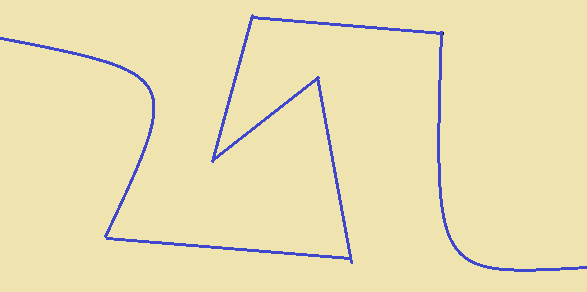
As linhas poligonais fechadas formam o que denominamos geralmente de figuras geométricas ou polígonos. Esse nome vem do grego: poli = mais de dois e gono = ângulo. Então a figura fechada com mais de dois ângulos é um polígono.
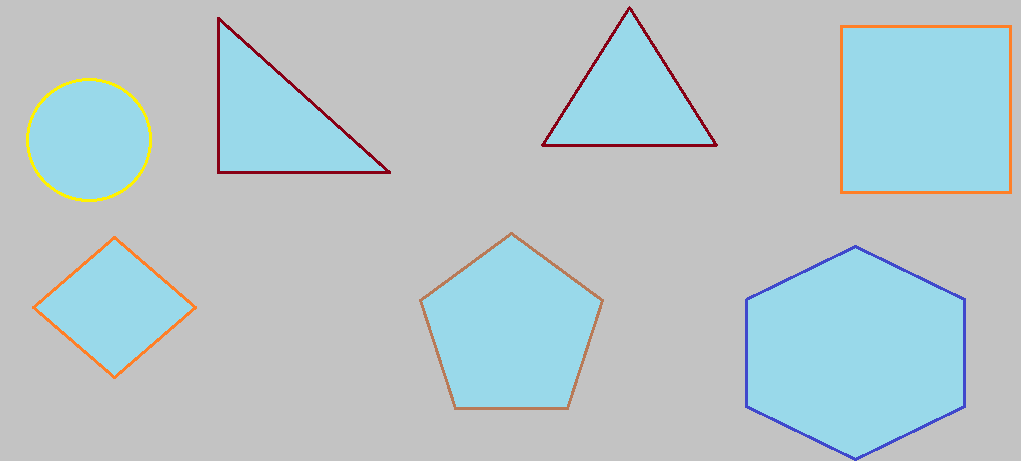
Polígonos regulares e irregulares
Regulares são os polígonos formados por lados iguais. Os lados são os segmentos de reta compreendidos entre dois ângulos consecutivos.
Irregulares são os polígonos formados por lados cujas medidas não são iguais.
Triângulos
Triângulo equilátero, que é também equiângulo é todo triângulo formado por três lados congruentes e em consequência os ângulos internos também são congruentes. Esses ângulos são todos agudos, isto é, medem menos de $90^{0}$.
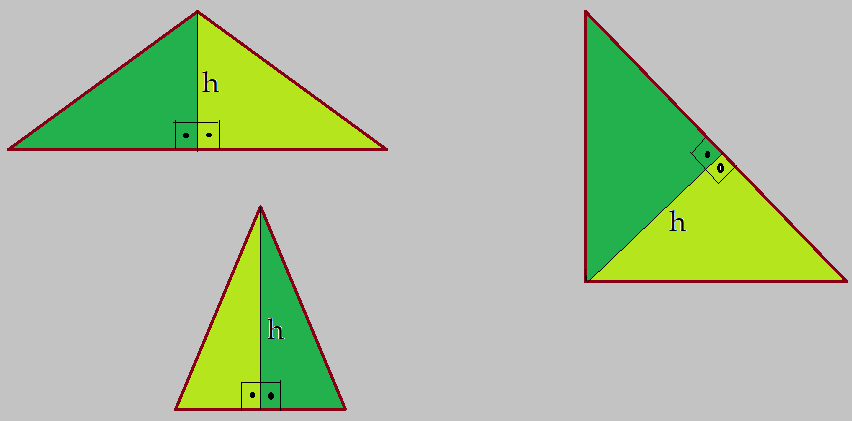
Triângulo isósceles: – é o triângulo que tem dois lados congruentes. A altura, traçada em relação ao lado oposto, divide o triângulo em dois triângulos retângulos congruentes.
Triângulo escaleno: – é o triângulo que tem os três lados com medidas diferentes. Pode ser retângulo, acutângulo ou obtusângulo.
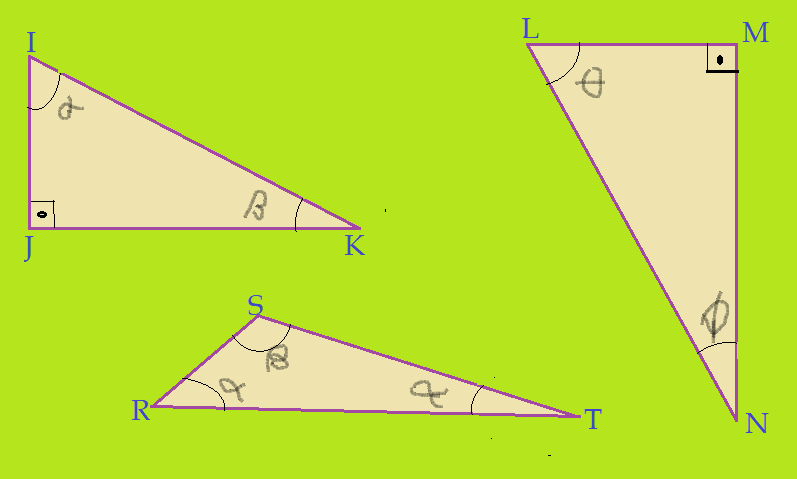
Triângulo retângulo: – tem necessariamente um ângulo reto, podendo os outros dois ser congruentes ou diferentes, mas sempre menores que$90^{0}$
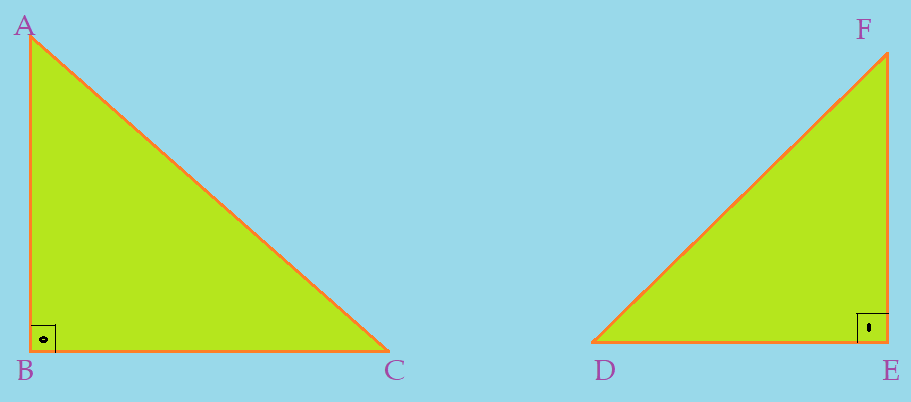
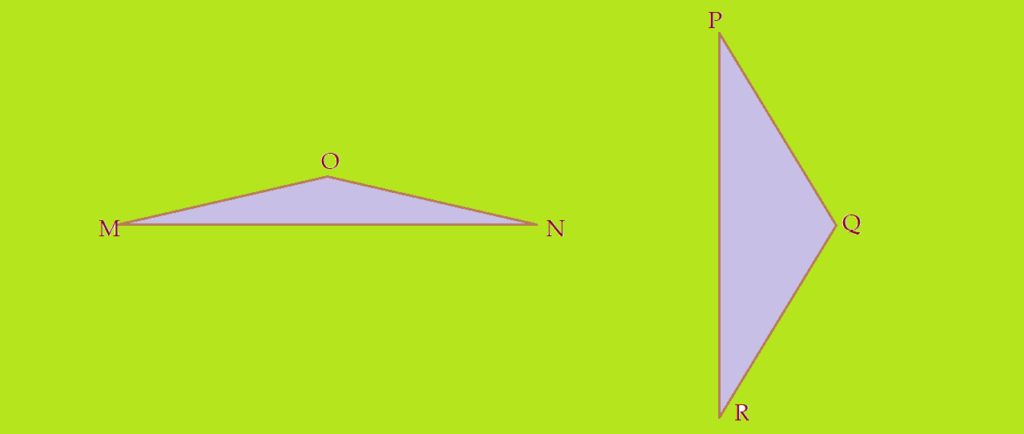
Triângulo obtusângulo: – tem um ângulo obtuso, sendo os outros dois agudos.
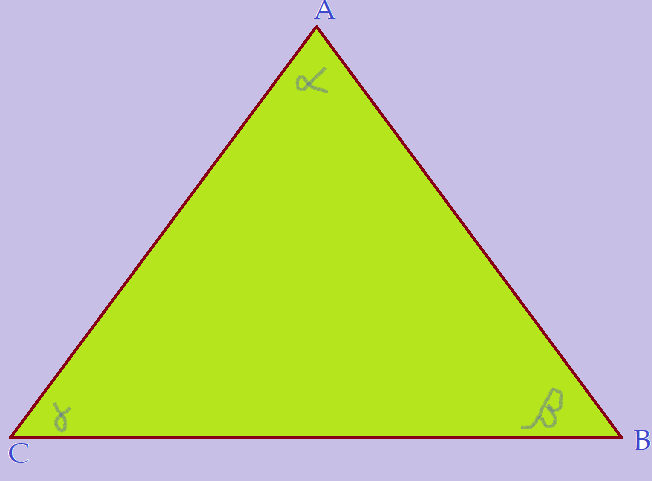
Soma dos ângulos internos do triângulo.
Vejamos a figura .
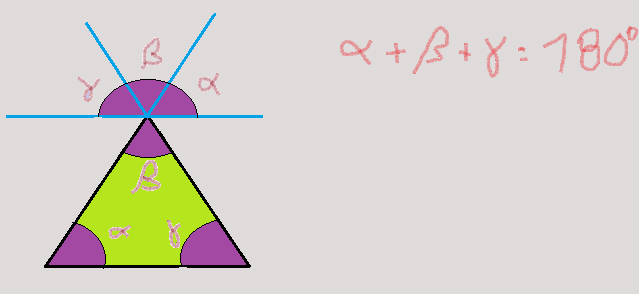
Como podemos observar na figura, os ângulos formados pelos prolongamentos dos dois lados e a paralela ao outro lado, passando pelo vértice oposto a ela, são respectivamente opostos pelo vértice e os outros dois são ângulos correspondentes, formados por uma transversal a retas paralelas. Os três ângulos completam exatamente um ângulo raso, ou seja $180^{0}$. Isso irá ocorrer com qualquer triângulo, não importando as medidas de seus ângulos internos. A soma dos mesmos será sempre a mesma. Dará $180^{0}$.
Podemos estabelecer que:
$\alpha \lt(\beta + \gamma)$
$\beta \lt (\alpha + \gamma)$
$\gamma \lt (\beta + \alpha)$
Também podemos estabelecer que cada ângulo é maior do que o módulo da diferença dos outros dois.
$\alpha \gt |\beta – \gamma|$
$\gamma \gt |\alpha – \beta|$
$\beta \gt |\alpha – \gamma|$
Segmentos notáveis num triângulo
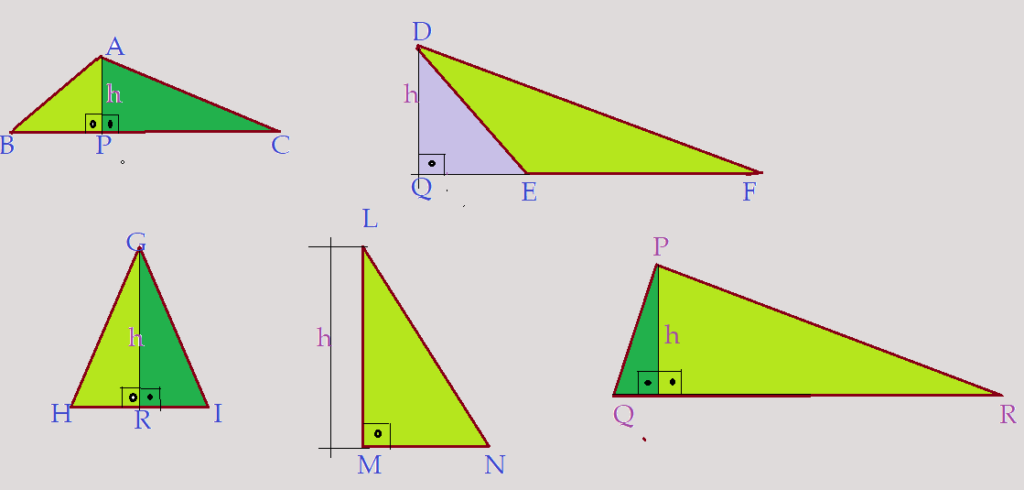
Altura: – é o segmento que une um vértice ao lado oposto formando com ele um ângulo reto. Como mostram as várias figuras, esse segmento pode estar localizado no interior do triângulo, como também pode estar fora, como acontece nos ângulos obtusângulos, quando é traçada em relação a um dos lados menores. Nos triângulos retângulos, as alturas em relação aos catetos, são os próprios. As alturas traçadas em relação aos três lados, se interceptam em um ponto, que pode estar localizado fora da figura. Este ponto é o chamado ortocentro do triângulo
Bissetriz: – denominamos bissetriz a reta ou segmento de reta que divide um ângulo ao meio. Todo triângulo possui três bissetrizes, que se interceptam em um ponto, no interior do polígono. A intersecção das bissetrizes denomina-se incentro, isto é, centro do compasso nesse ponto e abertura até qualquer um dos lados, pode-se traçar uma circunferência inscrita no interior do triângulo. Ela será tangente aos três lados do triângulo.
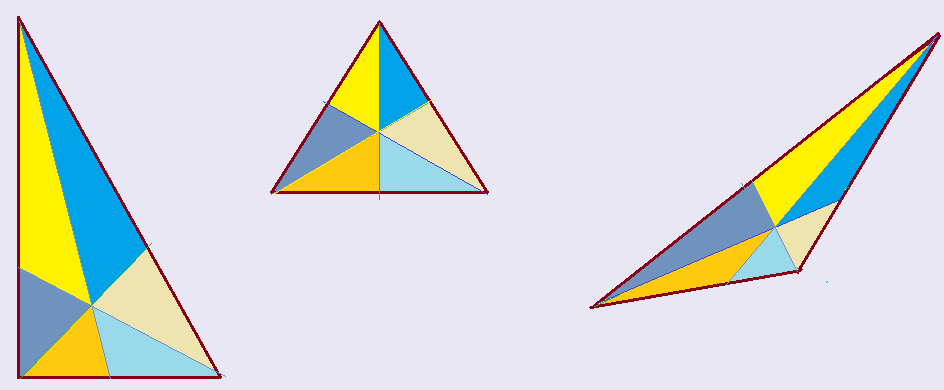
Obs.: O triângulo equilátero e equiângulo, é o único triângulo que pode ser denominado como figura geométrica regular. Por isso dedicaremos especial atenção a alguns detalhes. (Final.)
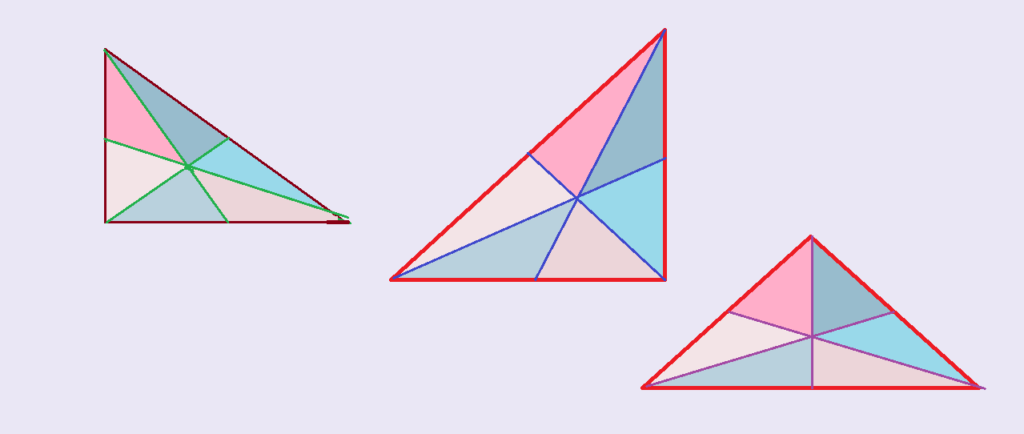
Medianas de um triângulo: – denominamos medianas as retas ou segmentos de reta que contém um vértice e o ponto médio do lado oposto a esse vértice, em qualquer triângulo. A intersecção das medianas determina o ponto denominado baricentro. Em outras palavras significa que uma lâmina triangular de material e espessura uniforme fica em equilíbrio se suspensa por esse ponto.
Mediatrizes de um triângulo: – são segmentos de reta levantados perpendicularmente ($90^{0}$) ao ponto médio de cada um dos lados do triângulo. A intersecção desses segmentos determina o ponto denominado circuncentro. Centrando o compasso nesse ponto e com abertura aos vértices, pode-se traçar uma circunferência circunscrita ao triângulo.
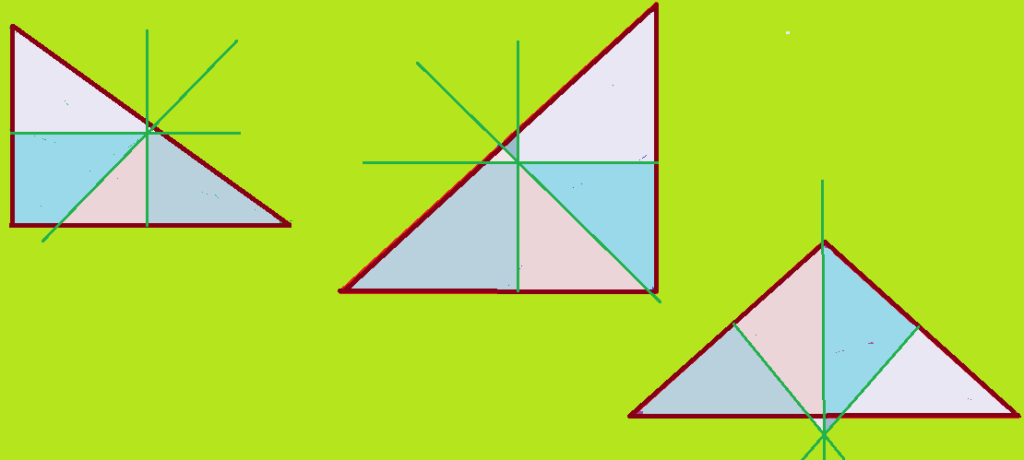
Triângulos semelhantes
Dois ou mais triângulos são semelhantes se eles tiverem ao menos dois ângulos congruentes. Como a soma dos ângulos internos de qualquer triângulo é sempre igual a $180^{0}$, a congruência entre dois ângulos, implica necessariamente que o terceiro ângulo também seja congruente.
Os triângulos semelhantes têm uma característica importante. A congruência entre seus ângulos faz com que os lados que formam os respectivos ângulos sejam proporcionais.
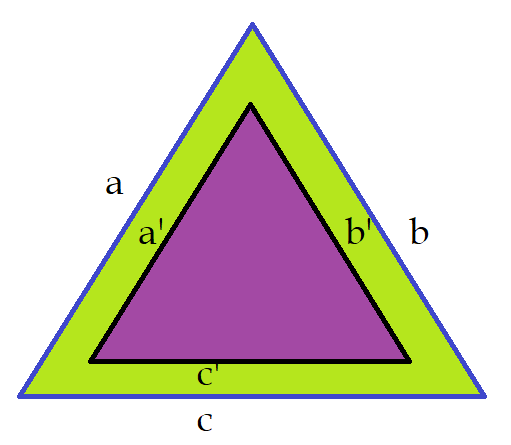
Observando os lados correspondentes podemos escrever a proporção:
$ {a\over a’} = {b\over b’} = {c\over c’}$
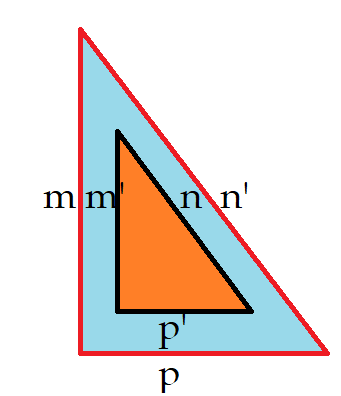
${m\over m’} = {n\over n’} = {p\over p’}$
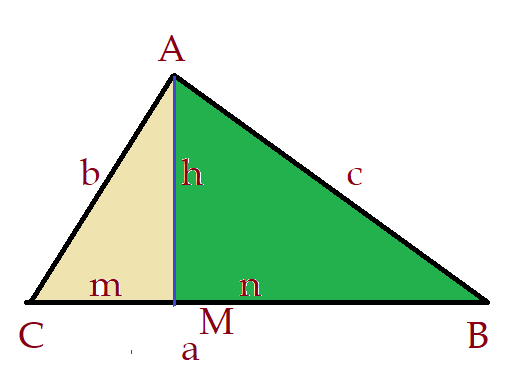
No triângulo retângulo, temos o angulo reto $\widehat{(BAC)}$, e os ângulos agudos $\widehat{(ABC)}$ e $\widehat{(ACB)}$. Ao traçar a altura $h$ passamos a ter dois triângulos retângulos com os ângulos retos adjacentes $\widehat{(AMB)}$ e $\widehat{(AMC)}$. Tanto o $\Delta{(AMBA)}$ quanto o $\Delta{(AMCA)}$ têm um ângulo comum com o $\Delta{(ABCA)}$. Sendo assim ambos são semelhantes ao triângulo maior e consequentemente são semelhantes entre si. Isso nos permite escrever a proporção:
${m\over h} = {h\over n}$$\Leftrightarrow$$ h² = m\cdot n$
Entre estas expressões a que mais usamos em aplicações variadas é a última, que costuma ser enunciada como:
“Num triângulo retângulo a altura relativamente à hipotenusa é média proporcional entre as projeções dos catetos sobre ela”.
Como demonstramos acima.
Triângulo áureo
O triângulo áureo básico é aquele que tem por hipotenusa um segmento cuja medida é igual à razão áurea $a = \Phi$. Os catetos são $b = \sqrt{\Phi}$ e $c = 1$. Todos os triângulos semelhantes a esse, quer sejam maiores ou menores são triângulos áureos. Seus lados serão respectivamente proporcionais.
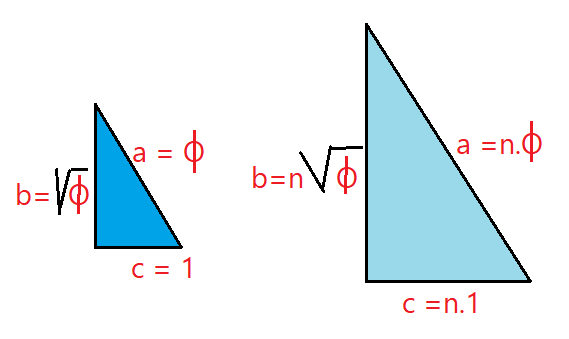
Podemos determinar os ângulos internos de qualquer triângulo áureo.
Por definição o ângulo entre os lados menores é reto. Mede $90^{0}$.
Os ângulos agudos são opostos aos catetos. Vejamos:
$sen^{-1}\gamma = \frac{\sqrt{\Phi}}{\Phi} = \frac{\sqrt{1,618}}{1,618}$
$\color{Navy}{sen^{-1}\gamma\simeq 51,828^{0}}$
$sen^{-1}\alpha = \frac{1}{\Phi} = \frac{1}{1,618}$
$\color{Navy}{sen^{-1}\alpha\simeq 38,172}$
Soma dos lados de um triângulo
Perímetro: – é a soma dos três lados do triângulo.
$p_{\Delta} = a + b + c$
Soma de dois lados: – em qualquer triângulo a soma de dois lados será sempre maior do que o terceiro lado.
$a \lt b + c$
$b \lt a + c$
$c \lt a + b$
Diferença entre dois lados: – o módulo da diferença entre dois lados de um triângulo é sempre menor do que o outro lado.
$|a – b| \lt c$
$|a – c| \lt b$
$|b – c| \lt a$
O triângulo retângulo tem uma característica importante, que veremos no próximo post. É uma figura geométrica de grande importância, com inúmeras situações em que se aplicam os conhecimentos a seu respeito.
Algumas perguntas para pensar?
- Um triângulo retângulo pode ser equilátero?
( ) sim; ( ) não; Porquê?…………………………………
2. Um triângulo escaleno pode ser retângulo?
( ) sim; ( ) não; Porquê?………………………………
3. Um triângulo equilátero pode ser obtusângulo?
( ) sim; ( ) não; Porquê? ……………………………………
4. Um triângulo isósceles pode ser retângulo?
( ) sim; ( ) nâo; Porquê? …………………………………
5. Um triângulo isósceles pode ser obtusângulo?
( ) sim; ( ) não; Porquê?…………………………………..
06. Um triangulo equilátero e um obtusângulo podem ser semelhantes? ( ) sim; ( )não; Porquê? ……………………………………………………………………………..
07. Se um triângulo deve ser construído com os lados medindo 3,0 cm, 5,0 m e 10,0 cm, é possível essa construção? ( )sim; ( )não; Porquê? Pense bem antes de responder. ………………………………………………………………………………………………..
08. Se a hipotenusa de um triângulo áureo mede $a = 5,0\,cm$, quais são as medidas de seus catetos?
09. O cateto menor de um triângulo áureo mede $c = 3,2\,cm$. Determine a medida do outro cateto e da hipotenusa.
10. A soma dos catetos de um triângulo áureo mede $b + c = 6,0\,cm$. Determine as medidas dos catetos e também da hipotenusa.
11. Um triângulo tem os lados $a = 8,0\, cm$ e $b= 6,0\,cm$. O terceiro lado mede tem sua medida em qual intervalo?
12. Em um triângulo um dos lados mede $15,0\,cm$. Quais os possíveis valores das medidas dos outros dois lados?
13. Se um dos ângulos de um triângulo mede $75^{0}$, quais são os possíveis valores das medidas dos outros dois ângulos?
14. Se um triângulo retângulo tem um ângulo agudo de $52^{0}$, quantos graus mede o outro ângulo agudo?
15. Se dois ângulos em um triângulo medem respectivamente $48^{0}$ e $62^{0}$, qual é a medida do terceiro ângulo?
16. Um triângulo tem dois lados medindo $a = 25,0\,cm$ e $b = 32,0\,cm$. Pergunta-se qual é o valor máximo que o perímetro desse triângulo pode ter?
Se ficaram dúvidas, faça a gentileza de entrar em contato por meio de um dos canais listados abaixo e vamos esclarecer o que não ficou entendido. OK?
Curitiba, 26 de outubro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e Whatsapp: (41) 99805-0732

