Multiplicar números com vírgulas.

Ao multiplicarmos números contendo vírgula, é quase certo de que o produto também conterá vírgula. Como iremos proceder para fazer essas multiplicações com segurança e sem errar?
Iremos colocar os números como se fossem inteiros e realizar a multiplicação da mesma forma. Feita a operação, iremos contar o número de algarismos existentes após a vírgula, tanto no multiplicando quanto no multiplicador e, contando esse número da direita para esquerda no produto, colocaremos a vírgula.

A melhor coisa é praticar para entender o assunto. Seja efetuar a multiplicação:
$\color{Blue}{(13,7)\cdot (2,8) = ?}$

Multiplicação de dois números decimais. A vírgula no produto é colocada contando duas casas da direita para esquerda, pois há nos fatores duas casas decimais (após a vírgula).

Fazemos de conta que estamos multiplicando $137$ por $28$. Depois contamos os algarismos após a vírgula e encontramos o resultado $2$. Da esquerda para direita, a vírgula vai se localizar após o algarismo $8$. Logo: $\color{Blue}{(13,7)\cdot (2,8) = 38,36 }$

Vamos a mais um exemplo: $\color{Blue}{(8,75)\cdot (0,42) =?}$
Fazendo a multiplicação em colunas.

Agora temos três algarismos (casas) após a vírgula nos fatores multiplicados e por isso contamos três casas da direita para esquerda onde colocaremos a vírgula no produto.

Como no outro exemplo, multiplicamos ignorando as vírgulas. Somente depois de concluir, contamos as casas decimais. Temos agora dois algarismos após a vírgula no multiplicando e dois no multiplicador. De modo que no produto iremos contar, da esquerda para direita, quatro casas e depois colocar a vírgula. Assim o resultado fica sendo; $\color{Blue}{(8,75)\cdot(0,42)) = 3,6750}$ Outro exemplo. $\color{Blue}{(43,7)\cdot(2,56) =?}$ Procedimento se repete.

Novamente três casas decimais após a vírgula.

Contando os algarismos decimais nos fatores, encontramos o total de três. Partindo da esquerda para direita, contamos três casas e colocamos a vírgula. O resultado fica então: $\color{Blue}{(43,7)\cdot(2,56) = 111,872}$ Para encerrar, mais um exemplo. $\color{Blue}{(7490)\cdot(0,075) =?}$

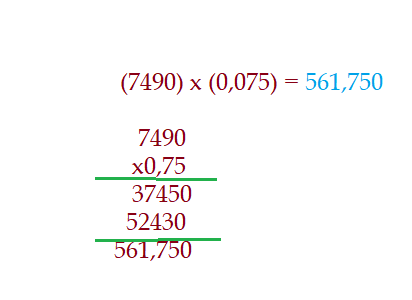
Temos três casas decimais e apenas um dos fatores, mas no outro não há nenhuma, pois é um número inteiro.

Os algarismos decimais agora estão apenas no multiplicador e são três. Isso nos dá como resultado da operação: $\color{navy}{(7490)\cdot(0,075) = 561,750}$ Vamos exercitar esse procedimento, efetuando as multiplicações a seguir.

$\color{Brown}{(82,46)\cdot (3,654) =?}$
$\color{Brown}{(753,4)\cdot(1,43) = ?}$
$\color{Brown}{(7,534)\cdot(14,3) = ?}$
$\color{Brown}{(6719)\cdot(0,0143) = ?}$
$\color{Brown}{(32,6)\cdot(3,49) = ?}$
$\color{Brown}{(8,32)\cdot(5,83) = ?}$
$\color{Brown}{(57,064)\cdot(1,73) = ?}$
$\color{Brown}{(9,452)\cdot(14) = ?}$
$\color{Brown}{(11,845)\cdot(5,753) = ?}$
$\color{Brown}{(96,24)\cdot(1,043) = ?}$
$\color{Brown}{(104,74)\cdot(9,72) = ?}$
$\color{Brown}{(6752)\cdot(32,5) = ?}$
$\color{Brown}{(75,2)\cdot(6,45) = ?}$
$\color{Brown}{(43,751)\cdot(3,75) =?}$
$\color{Brown}{(914,76)\cdot(54,7) =?}$
$\color{Brown}{(1075,2)\cdot(0,0048) +?}$
$\color{Brown}{(8534,9)\cdot(7,25) =?}$

Obs.: Se tiver dúvidas, entre em contato por um dos canais que constam abaixo para resolver qualquer questão. Não fique com dúvidas.

Curitiba, 08 de setembro de 2016. Atualizado e revisado em 03 de outubro de 2019

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732