Tabela resumo das relações trigonométricas
| Lista das principais relações trigonométricas |
| $\color{blue}{sen^2\alpha + cos^2\alpha = 1}$ |
| $\color{blue}{tg\alpha = {{sen\alpha}\over cos\alpha}}$ |
| $\color{blue}{ctg\alpha = {{cos\alpha}\over sen\alpha}}$ |
| $\color{blue}{ctg\alpha = {1\over tg\alpha}}$ |
| $\color{blue}{csc\alpha = {1\over sen\alpha}}$ |
| $\color{blue}{sec\alpha = {1\over cos\alpha}}$ |
| $ \color{blue}{csc\alpha = \sqrt{1 + ctg^2\alpha}}$ |
| $ \color{blue}{sec\alpha = \sqrt{1 + tg^2\alpha}}$ |
| $ \color{blue}{cos\alpha = {(1 + tg^2\alpha)}^{-{1\over2}}}$ |
| $ \color{blue}{sen\alpha = {(1 + ctg²\alpha)}^{-{1\over2}}}$ |
| $ \color{blue}{{a\over sen\alpha} = {b\over sen\beta} = {c\over sen\gamma} = 2r}$ |
| $ \color{blue}{a^2 = b^2 + c^2 – 2bc\cdot cos\alpha}$ |
| $ \color{blue}{b^2 = a^2 + c^2 – 2ac\cdot cos\beta}$ |
| $ \color{blue}{c^2 = a^2 + b^2 – 2ab\cdot cos\gamma}$ |
| $ \color{blue}{sen{(\alpha\pm\beta)} = sen\alpha\cdot cos\beta \pm sen\beta\cdot cos\alpha}$ |
| $ \color{blue}{cos{(\alpha\pm\beta)} = cos\alpha\cdot} cos\beta\mp sen\alpha\cdot sen\beta$ |
| $ \color{blue}{tg{(\alpha\pm\beta)}={{1\pm tg\beta\cdot ctg\alpha}\over{ctg\alpha\mp tg\beta}}}$ |
| $ \color{blue}{ctg{(\alpha\pm\beta)} = {{ctg\alpha\mp tg\beta}\over{1\pm tg\beta\cdot ctg\alpha}}}$ |
| $\color{blue}{sec{(\alpha\pm\beta)} = {1\over{cos\alpha\cdot cos\beta\mp sen\beta\cdot sen\alpha}}}$ |
| $\color{blue}{csc{(\alpha\pm\beta)} = {1\over{sen\alpha\cdot cos\beta\pm sen\beta\cdot cos\alpha}}}$ |
| $ \color{blue}{sen{(2\alpha)} = 2\cdot sen\alpha\cdot cos\alpha}$ |
| $ \color{blue}{cos{(2\alpha)} = cos^2\alpha – sen^2\alpha}$ |
| $ \color{blue}{tg{(2\alpha)} = {2\over{ctg\alpha – tg\alpha}}}$ |
| $ \color{blue}{ctg{(2\alpha)} = {{ctg\alpha – tg\alpha}\over 2}}$ |
| $ \color{blue}{csc{(2\alpha)} = {(2sen\alpha\cdot cos\alpha)}^{-{1\over 2}}}$ |
| $ \color{blue}{sec{(2\alpha)} = {(cos^2\alpha – sen^2\alpha)}^{-{1\over 2}}}$ |
Vamos exercitar.
01. Um dos ângulos agudos de um triângulo tem como $sen\alpha = {\sqrt{5}\over 4}$. Determine: a) o cosseno desse ângulo; b) a tangente e cotangente desse ângulo; c) a secante e cossecante desse ângulo.
a) A relação fundamental nos diz que:
$\color{navy}{sen^2\alpha + cos^2\alpha = 1}$
Se $sen\alpha = {\sqrt{5}\over 4}$, teremos:
${\left(\sqrt{5}\over4\right)}^2 + cos^2\alpha = 1$$\Leftrightarrow$$ {5\over{16}} + cos^2\alpha = 1$
$cos^2\alpha = 1 – {5\over{16}}$$\Leftrightarrow$$cos^2\alpha = {{16 – 5}\over {16}}$
$\sqrt{cos^2\alpha} =\sqrt{{11}\over{16}}$$\Leftrightarrow$$cos\alpha = {\sqrt{11}\over\sqrt{16}}$
$\color{maroon}{cos\alpha = {\sqrt{11}\over 4}}$
b) dispondo do seno e cosseno, podemos facilmente determinar a tangente e cotangente.
$\color{navy}{tg\alpha = {sen\alpha\over cos\alpha}}$
$tg\alpha = \left[\left({\sqrt{5}\over 4}\right)\over\left({\sqrt{11}\over 4}\right)\right]$$\Leftrightarrow$$tg\alpha = {\left(\sqrt{5}\over 4\right)}\cdot{\left(4\over \sqrt{11}\right)}$
$tg\alpha = {{\sqrt{5}}\over{\sqrt{11}}}$$\Leftrightarrow$$tg\alpha = \left({{\sqrt{5}\cdot\sqrt{11}}\over{\sqrt{11}}^2}\right)$
$\color{maroon}{ta\alpha = {\sqrt{55}\over{11}}}$
$\color{navy}{ctg\alpha = {cos\alpha\over sen\alpha}}$
$ctg\alpha = \left[{\left({\sqrt{11}\over 4}\right)\over\left({\sqrt{5}\over 4}\right)}\right]$$\Leftrightarrow$$ctg\alpha = \left[{\left(\sqrt{11}\over 4\right)}\cdot\left({4\over\sqrt{5}}\right)\right]$
$ctg\alpha = \left[{\sqrt{11}\over\sqrt{5}}\right]$$\Leftrightarrow$$ctg\alpha = \left[\left({\sqrt{11}\cdot\sqrt{5}}\right)\over\left({\sqrt{5}}^2\right)\right]$
$\color{maroon}{ctg\alpha = {\sqrt{55}\over 5}}$
c) faltam apenas a secante e cossecante. Isso é fácil.
$\color{navy}{csc\alpha = {1\over sen\alpha}}$
$csc\alpha = \left[{1\over{\left(\sqrt{5}\over 4\right)}}\right]$
$csc\alpha = \left[{\left(4\over\sqrt{5}\right)}\right]$$\Leftrightarrow$$csc\alpha = \left[{\left(4\cdot\sqrt{5}\right)\over{\sqrt{5}^2}}\right]$
$\color{maroon}{csc\alpha = {4\cdot\sqrt{5}\over 5}}$
$\color{navy}{sec\alpha = {1\over cos\alpha}}$
$sec\alpha = \left[{1\over\left({\sqrt{11}\over 4}\right)}\right]$$\Leftrightarrow$$sec\alpha = \left[{\left(4\over\sqrt{11}\right)}\right]$
$sec\alpha = \left[{\left(4\cdot\sqrt{11}\right)\over{\sqrt{11}^2}}\right]$$\Leftrightarrow$$sec\alpha = {4\cdot\sqrt{11}\over 11}$
$\color{maroon}{sec\alpha = {4\cdot\sqrt{11}\over 11}}$
02. Se a $tg\beta = \frac{\sqrt{5}}{5}$, determine a cotangente, a secante e cossecante.
$\color{BlueViolet}{ctg\beta = \frac{1}{tg\beta}}$
$ctg\beta = \left[\frac{1}{\left(\frac{\sqrt{5}}{5}\right)}\right]$$\Leftrightarrow$$ctg\beta = \left[\frac{5}{sqrt{5}}\right]$
$ctg\beta = \left[\left(\frac{5\cdot\sqrt{5}}\right){\sqrt{5}^2}\right]$$\Leftrightarrow$$ctg\beta = \left[\frac{5\cdot \sqrt{5}}{5}\right]$
$\color{Bittersweet}{ctg\beta = \sqrt{5}}$
$\color{navy}{sec\beta = \sqrt{1 + tg^2\beta}}$
$sec\beta =\left[ \sqrt{1 + {\left(\frac{\sqrt{5}}{5}\right)^2}}\right]$$\Leftrightarrow$$sec\beta =\left[\sqrt {1 + \left\(\frac{5}\over{25}\right)}\right]$
$sec\beta = \left[\sqrt{\left({{25} + 5}\right)\over {25}}\right]$$\Leftrightarrow$$sec\beta =\left[\sqrt {{30}\over{25}}\right]$
$\color{Bittersweet}{sec\beta = \frac{\sqrt{30}}{5}}$
$\color{navy}{csc\beta = \sqrt{1 + ctg^2\beta}}$
$csc\beta = \left[\sqrt{1 + \sqrt{5}^2}\right]$$\Leftrightarrow$$csc\beta = \sqrt{1 + 5}$
$\color{Bittersweet}{csc\beta = \sqrt{6}}$
03. Considerando $sen\alpha = {1\over2}$ e $sen\beta = {\sqrt{2}\over2}$, determine: a) $sen{(\alpha + \beta)}$; b) $cos{(\alpha + \beta)}$; c) $tg{(\alpha + \beta)}$; d) $ctg{(\alpha + \beta)}$; e) $sec{(\alpha + \beta)}$; f) $csc{(\alpha + \beta)}$
a) seno de ${(\alpha + \beta)}$
$\color{navy}{sen{(\alpha + \beta)} = {sen\alpha\cdot cos\beta + sen\beta\cdot cos\alpha}}$
Temos que determinar primeiramente o cosseno dos dois ângulos, aplicando a relação fundamental, além da tangente e cotangente.
$\color{navy}{sen^2\alpha + cos^2\alpha = 1}$
$({1\over2})^2 + cos^2\alpha + 1$
${1\over 4} + cos^2\alpha = 1$$\Leftrightarrow$$cos^2\alpha = 1 – {1\over4}$
$cos^2\alpha = {{4 – 1}\over 4}$$\Leftrightarrow$${cos^2\alpha} = {3\over 4}$
$\sqrt{cos^2\alpha} = \sqrt{3\over4}$
$\color{maroon}{cos\alpha = {\sqrt{3}\over 2}}$
$\color{BlueViolet}{sen^2\beta + cos^2\beta = 1}$
$ \left({\sqrt{2}\over 2}\right)^2 + cos^2\beta = 1$$\Leftrightarrow$$ {\not{2}^1\over \not{4}^2} + cos^2\beta = 1$
$cos^2\beta = 1 – {1\over2} = {{2 – 1}\over 2}$
$cos^2\beta = {1\over 2}$$\Leftrightarrow$$\sqrt{cos^2\beta} = \sqrt{1\over{2}}$
$cos\beta = {1\over\sqrt{2}} = {{1\cdot\sqrt{2}}\over{\sqrt{2}}^2}$
$\color{maroon}{cos\beta = {\sqrt{2}\over2}}$
$\color{navy}{tg\alpha = {{sen\alpha}\over{cos\alpha}}}$
$tg\alpha = \left({{1\over 2}\over{\sqrt{3}\over 2}}\right)$$\Leftrightarrow$$tg\alpha = \left({{1\over 2}\cdot{2\over\sqrt{3}}}\right)$=${1\cdot\sqrt{3}\over\sqrt{3}^2}$
$\color{maroon}{tg\alpha = {\sqrt{3}\over 3}}$
$\color{navy}{ctg\alpha = {1\over tg\alpha}}$
$ctg\alpha = \left({1 \over{\sqrt{3}\over 3}}\right)$$\Leftrightarrow$$ctg\alpha = {3\over\sqrt{3}} = {3\sqrt{3}\over{\sqrt{3}^2}}$
$\color{maroon}{ctg\alpha = \sqrt{3}}$
$\color{navy}{tg\beta = {sen\beta\over cos\beta}}$
$tg\beta =\left[{\left({\sqrt{2}\over 2}\right)\over\left({\sqrt{2}\over2}\right)}\right]$
$tg\beta = \left[{\left({\not{\sqrt{2}}^1\over\not{2}^1}\right)\cdot{\left({\not{2}^1\over\not{\sqrt{2}}^1}\right)}}\right]$
$\color{maroon}{tg\beta = 1}$
$\color{navy}{ctg\beta = {1\over tg\beta}}$
$ctg\beta = {1\over 1} = 1$
$\color{maroon}{ctg\beta = 1}$
$\color{blue}{csc\alpha = {1\over sen\alpha}}$
$ csc\alpha = {1\over {1\over 2}}$
$\color{maroon}{csc\alpha = 2}$
$\color{blue}{csc\beta = {1\over{sen\beta}}}$
$ csc\beta = {1 \over{\sqrt{2}\over 2}}$$\Leftrightarrow$$csc\beta = {2\over\sqrt{2}}$
$csc\beta = {2\sqrt{2}\over\sqrt{2}^2}$$\Leftrightarrow$$csc\beta = {2\sqrt{2}\over 2}$
$\color{maroon}{csc\beta = \sqrt{2}}$
$\color{blue}{sec\alpha = {1\over cos\alpha}}$
$sec\alpha = {1\over{\sqrt{3}\over 2}}$$\Leftrightarrow$$sec\alpha = {2\over\sqrt{3}}$
$sec\alpha = {2\cdot\sqrt{3}\over \sqrt{3}^2}$$\Leftrightarrow$$sec\alpha ={2\sqrt{3}\over 3}$
$\color{maroon}{sec\alpha = {2\cdot\sqrt{3}\over 3}}$
$\color{blue}{sec\beta = {1\over cos\beta}}$
$sec\beta = {1\over{\sqrt{2}\over 2}}$$\Leftrightarrow$$sec\beta = {2\over \sqrt{2}}$
$sec\beta = {2\cdot \sqrt{2}\over\sqrt{2}^2}$$\Leftrightarrow$$sec\beta = {2\sqrt{2}\over 2}$
$\color{maroon}{sec\beta = \sqrt{2}}$
$sen{(\alpha + \beta)} = {{1\over2}\cdot{\sqrt{2}\over 2}} + {{\sqrt{2}\over 2}\cdot {\sqrt{3}\over2}}$
$sen{(\alpha + \beta)} = {\sqrt{2}\over 4} + {\sqrt{6}\over 4}$
$\color{maroon}{sen{(\alpha + \beta)} = {{\sqrt{2} + \sqrt{6}}\over 4}}$
b) cosseno de ${(\alpha + \beta)}$
$cos{(\alpha + \beta)} = {{\sqrt{3}\over 2}\cdot {\sqrt{2}\over 2} – {{1\over2}\cdot {\sqrt{2}\over 2}}}$
$cos{(\alpha + \beta)} = {{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}$
$\color{maroon}{cos{(\alpha + \beta)} = {{\sqrt{6} – \sqrt{2}}\over4}}$
c) tangente de ${(\alpha + \beta)}$
$ \color{marine}{tg{(\alpha\pm\beta)}={{1\pm tg\beta\cdot ctg\alpha}\over{ctg\alpha\mp tg\beta}}}$
$tg{(\alpha + \beta)} = {{1 + {1\cdot\sqrt{3}}}\over{{\sqrt{3} – 1}}}$
$tg{(\alpha + \beta)} =\left[{\left({{1 + \sqrt{3}}}\right)\over\left({\sqrt{3} -1}\right)}\right]$
Racionalizando o denominador:
$tg{(\alpha + \beta)} = \left[{\left({\sqrt{3} + 1}\right)\over\left({\sqrt{3} – 1}\right)}\right]\cdot\left[{\left({\sqrt{3} + 1}\right)\over\left({\sqrt{3} + 1}\right)}\right]$
$tg{(\alpha + \beta)} = \left[{\left({\sqrt{3}^2 + 2\sqrt{3} + 1}\right)\over\left({\sqrt{3}^2 – 1^2}\right)}\right]$$\Leftrightarrow$$tg{(\alpha + \beta)} = \left[{\left({3 + 2\sqrt{3} + 1}\right)\over\left({3 – 1}\right)}\right]$
$tg{(\alpha + \beta)} = \left[{{2\sqrt{3} + 4}\over{2}}\right]$
$\color{maroon}{tg{(\alpha + \beta)} = {\sqrt{3} + 2}}$
d) cotangente de ${(\alpha + \beta)}$
$\color{navy}{ctg{(\alpha + \beta)}= \left({{ctg\alpha – tg\beta}\over{1 + tg\beta\cdot ctg\alpha}}\right)}$
$ctg{(\alpha + \beta)} =\left[{\left({\sqrt{3} – 1}\right)\over{1 + \left({1\cdot\sqrt{3}}\right)}}\right]$$\Leftrightarrow$$ctg{(\alpha + \beta)} = \left[{{(\sqrt{3} – 1)}\cdot{(\sqrt{3} – 1)}\over{(\sqrt{3} + 1)}\cdot {(\sqrt{3} – 1)}}\right]$
$ctg{(\alpha + beta)} = \left[{{(\sqrt{3} – 1)}^2\over{(\sqrt{3}^2 – 1^2)}}\right]$$\Leftrightarrow$$ctg{(\alpha + \beta)} = \left[{
{(3 – 2\sqrt{3} +1)}\over 2}\right]$
$ctg{(\alpha + \beta)} = \left({{4 – 2\sqrt{3}}\over 2}\right) = {2 -\sqrt{3}}$
$\color{maroon}{ctg{(\alpha + \beta)} = {2 – \sqrt{3}}}$
e)secante ${(\alpha + \beta)}$
$\color{navy}{sec{(\alpha + \beta)} = \left[{{1} \over\left({{cos\alpha\cdot cos\beta} – {sen\alpha\cdot sen\beta}}\right)}\right]}$
$sec{(\alpha + \beta)} = \left[{{1}\over\left({{{\sqrt{3}\over 2}\cdot{\sqrt{2}\over 2}} – {{1\over 2}\cdot {\sqrt{2}\over 2}}}\right)}\right]= \left[{{1}\over\left({{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}\right)}\right]$*
$sec{(\alpha + \beta)} = \left({{4}\over{\sqrt{6} – \sqrt{2}}}\right)$=$\left[{{4\cdot\left({\sqrt{6} + \sqrt{2}}\right)}\over{\left({\sqrt{6} – \sqrt{2}}\right)}\cdot\left({\sqrt{6} + \sqrt{2}}\right)}\right]$
$sec{(\alpha + \beta)} = \left[{{4\cdot\left({\sqrt{6} + \sqrt{2}}\right)}\over\left({6 – 2}\right)}\right] = \left[{{4\cdot\left({\sqrt{6} + \sqrt{2}}\right)}\over 4}\right]$
$\color{maroon}{sec{(\alpha + \beta)} = {\sqrt{6} + \sqrt{2}}}$
f) cossecante de ${(\alpha + \beta)}$
$\color{navy}{csc{(\alpha + \beta)} = \left({{1}\over{{sen\alpha\cdot cos\beta} + {sen\beta\cdot cos\alpha}}}\right)}$
$csc{(\alpha + \beta)} = \left[{{1}\over\left({{1\over 2}\cdot {\sqrt{2}\over 2} + {\sqrt{2}\over 2}\cdot{\sqrt{3}\over 2}}\right)}\right]$=$\left[{{1}\over\left({{\sqrt{2}\over 4} + {\sqrt{6}\over 4}}\right)}\right]$
$csc{(\alpha + \beta)} = \left[{{1}\over\left({{\sqrt{2} + \sqrt{6}}\over 4}\right)}\right]$=$\left[{{4}\over\left({\sqrt{2} + \sqrt{6}}\right)}\right]$
$csc{(\alpha + \beta)} = \left[{{4\cdot\left({\sqrt{2} – \sqrt{6}}\right)}\over\left({\sqrt{2} + \sqrt{6}}\right)\cdot\left({\sqrt{2} – \sqrt{6}}\right)}\right]$=$\left[{{4\cdot\left({\sqrt{2} – \sqrt{6}}\right)}\over\left({2 – 6}\right)}\right]$
$csc{(\alpha + \beta)} = \left[{{4\cdot\left({\sqrt{2} – \sqrt{6}}\right)}\over {- 4}}\right]$=$\left[{{\sqrt{2} – \sqrt{6}}\over {-1}}\right]$
$\color{maroon}{csc{(\alpha + \beta)} = {\sqrt{6} – \sqrt{2}}}$
04. Sabe-se que $\color{blue}{cos\alpha ={1\over 2}}$ e $\color{blue}{sen\beta ={\sqrt{2}\over 2}}$. Determine: a) $\color{blue}{sen{(\alpha – \beta)}}$; b) $\color{blue}{cos{(\alpha – \beta)}}$; c) $\color{blue}{tg{(\alpha – beta)}}$; d)$\color{blue}{ctg{(\alpha – beta)}}$; e)$\color{blue}{csc{(\alpha – beta)}}$ e $\color{blue}{sec{(\alpha – beta)}}$.
Novamente começaremos por determinar o seno e o cosseno de $\alpha$ e $\beta$.
Temos que: $\color{brown}{cos\alpha = {1\over 2}}$
$\color{blue}{sen²\alpha + cos²\alpha = 1}$
Substituímos: $sen^2\alpha + {\left(1\over 2\right)}^2 = 1$$\Leftrightarrow$$sen^2\alpha + {1\over 4} = 1$
$sen^2\alpha = {1 – {1\over 4}}$$\Leftrightarrow$$sen^2\alpha = {3\over 4}$
$\sqrt{sen^2\alpha} = \sqrt{3\over 4}$$\Leftrightarrow$$sen\alpha ={\sqrt{3}\over\sqrt{4}}$
$\color{maroon}{sen\alpha = {\sqrt{3}\over 2}}$
Temos também que: $\color{blue}{sen\beta = {\sqrt{2}\over2}}$
Substituindo na relação fundamental: $\color{navy}{sen^2\beta + cos^2\beta = 1}$
$\left({\sqrt{2}\over 2}\right)^2+ cos^2\beta = 1$
$\left({\not{2}^1\over\not{4}^2}\right) + cos^2\beta = 1$$\Leftrightarrow$$cos^2\beta = {1 – {1\over 2}}$
$\sqrt{cos^2\beta} = {\sqrt{1\over 2}}$$\Leftrightarrow$$cos\beta = {\sqrt{1}\over\sqrt{2}}$
$cos\beta = {1\over\sqrt{2}}= {1\cdot\sqrt{2}\over\sqrt{2}^2}$
$\color{maroon}{cos\beta = {\sqrt{2}\over2}}$
Agora podemos determinar:
$\color{blue}{sen{(\alpha – \beta)} = {sen\alpha\cdot cos\beta – sen\beta\cdot cos\alpha}}$
$sen{(\alpha – \beta)}={{\sqrt{3}\over2}\cdot{\sqrt{2}\over2} – {\sqrt{2}\over 2}\cdot{1\over 2}}$=${{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}$
$\color{maroon}{sen{(\alpha – \beta)} = {{\sqrt{6} -\sqrt{2}}\over 4}}$
b)Também podemos determinar$\color{brown}{cos{(\alpha – \beta)}}$.
$\color{navy}{cos{(\alpha – \beta)} = {{cos\alpha\cdot cos\beta} + {sen\alpha\cdot sen\beta}}}$
$cos{(\alpha – \beta)} = {({1\over2})\cdot({\sqrt{2}\over 2})+({\sqrt{3}\over2})\cdot({\sqrt{2}\over 2})}$=${({\sqrt{2}\over4}) + ({\sqrt{6}\over 4})}$
$\color{maroon}{cos{(\alpha – \beta)} = {{\sqrt{2} + \sqrt{6}}\over 4}}$
c) Vamos determinar $\color{blue}{tg{(\alpha – \beta)}}$
Começaremos por determinar:
$\color{blue}{tg\alpha}$; $\color{blue}{tg\beta}$; $\color{blue}{ctg\alpha}$ e $\color{blue}{ctg\beta}$
$\color{blue}{tg\alpha = {{sen\alpha}\over {cos\alpha}}}$
$tg\alpha = \left[{\left({\sqrt{3}\over 2}\right)\over\left({1\over2}\right)}\right]$$\Leftrightarrow$$tg\alpha = \left[{\left({\sqrt{3}\over2}\right)\cdot\left({1\over2}\right)}\right]$
$\color{maroon}{tg\alpha = {\sqrt{3}\over 4}}$
$\color{blue}{tg\beta = \left[{\left({sen\beta}\right)\over\left({cos\beta}\right)}\right]}$
$tg\beta =\left[{\left({\sqrt{2}\over 2}\right)\over\left({\sqrt{2}\over2}\right)}\right]$
$\color{maroon}{tg\beta = 1}$
$\color{blue}{ctg\alpha = {cos\alpha\over sen\alpha}}$
$ctg\alpha = \left[{\left({1\over2}\right)\over\left({\sqrt{3}\over2}\right)}\right]$ $\Leftrightarrow$$ ctg\alpha = \left[{\left({1\over 2}\right)\cdot\left({2\over \sqrt{3}}\right)}\right]$
$ctg\alpha = \left[{\left({1\cdot\not{2}}\right)\over\left({\not{2}\cdot\sqrt{3}}\right)}\right]$$\Leftrightarrow$$ctg\alpha = {1\over\sqrt{3}} = {{1\cdot\sqrt{3}}\over\sqrt{3}^2}$
$\color{maroon}{ctg\alpha = {\sqrt{3}\over 3}}$
$\color{navy}{ctg\beta ={{cos\beta}\over{sen\beta}}}$
$ctg\beta = \left[{\left({\sqrt{2}\over 2}\right)\over\left({\sqrt{2}\over 2}\right)}\right]$
$\color{maroon}{ctg\beta = 1}$
$\color{blue}{tg{(\alpha – \beta)} = \left[{\left({1 – tg\beta\cdot ctg\alpha}\right)\over\left({ctg\alpha + tg\beta}\right)}\right]}$
$tg{(\alpha – \beta)} =\left[{{1 + \left({1\cdot\sqrt{3}\over 3}\right)}}\over{\left({{\sqrt{3}\over 3} + 1}\right)}\right]$$\Leftrightarrow$$tg{(\alpha – \beta)} = \left[{{\left({1 + \sqrt{3}}\right)\over3}\over{\left({\sqrt{3}\over3} + 1}\right)}}\right]$
$tg{(\alpha – \beta)}=\left[{\left({{3 + \sqrt{3}}\over\not{3}}\right)\cdot\left({\not{3}\over\sqrt{3}}\right)}\right]$$\Leftrightarrow$$tg{(\alpha – \beta)} = \left[{{\left({3 +\sqrt{3}}\right)\cdot\sqrt{3}}\over{\sqrt{3} +{3}}}\right]$=$\left[{{3\sqrt{3} +\sqrt{3}^2}\over\sqrt{3}^2}\right]$
$tg{(\alpha – \beta)}=\left[{{3\sqrt{3} + 3}\over 3}\right]={\sqrt{3} + 1}$
$\color{maroon}{tg{(\alpha – \beta)} = {\sqrt{3} + 1}}$
d) Agora a cotangente $\color{blue}{(\alpha – \beta)}$
$ \color{blue}{ctg{(\alpha\pm\beta)} = {{ctg\alpha\mp tg\beta}\over{1\pm tg\beta\cdot ctg\alpha}}}$
$ctg{(\alpha – \beta)}=\left[{\left({{\sqrt{3}\over3} + 1}\right)\over\left({1 – 1\cdot{\sqrt{3}\over3}}\right)}\right]$=$\left[{\left({{\sqrt{3} + 3}\over3}\right)\over\left({{3 -\sqrt{3}}\over3}\right)}\right]$
$ctg{(\alpha -\beta)} = \left[{\left({{\sqrt{3} + 3}\over\not{3}}\right)\cdot\left({\not{3}\over{\sqrt{3} – 3}}\right)}\right]$
$ctg{(\alpha – \beta)}=\left[{({\sqrt{3} +3})\cdot({\sqrt{3} + 3})\over({\sqrt{3}-3})\cdot({\sqrt{3}+3})}\right]$
$ctg{(\alpha-\beta)}=\left[{({\sqrt{3}^2 + 6\cdot\sqrt{3} + 9})\over({\sqrt{3}^2 – 9})}\right]$
$ctg{(\alpha – \beta)} = {{12 + 6\sqrt{3}}\over{3 – 9}}$=${{12 + 6\sqrt{3}}\over{-6}}$
$\color{maroon}{ctg{(\alpha-\beta)} = {\sqrt{3} – 2}}$
e) Vamos à secante $\color{blue}{(\alpha-\beta)}$
$\color{blue}{sec{(\alpha\pm\beta)} = {1\over{cos\alpha\cdot cos\beta\mp sen\beta\cdot sen\alpha}}}$
$sec{(\alpha-\beta)}=\left[{1\over{{1\over2}\cdot{\sqrt{2}\over2} +{\sqrt{3}\over2}\cdot {\sqrt{2}\over2}}}\right]$=$\left[{1\over{{\sqrt{2}\over4}+{\sqrt{6}\over4}}}\right]$
$sec{(\alpha-\beta)}=\left({4\over{\sqrt{2} + \sqrt{6}}}\right)$=$\left[{4\cdot\left({\sqrt{2}-\sqrt{6}}\right)\over{\left({\sqrt{2} +\sqrt{6}}\right)\cdot\left({\sqrt{2} -\sqrt{6}}\right)}}\right]$
$sec{(\alpha-\beta)}=\left[{4\cdot\left({\sqrt{2} -\sqrt{6}}\right)\over\left({\sqrt{2}^2 – \sqrt{6}^2}\right)}\right]$=$\left[{4\cdot\left({\sqrt{2} -\sqrt{6}}\right)\over{2 – 6}}\right]$
$sec{(\alpha-\beta)}=\left[{\not{4}\cdot\left({\sqrt{2} – \sqrt{6}}\right)\over {-\not{4}}}\right]$=${-{\left(\sqrt{2} – \sqrt{6}\right)}}$
$\color{maroon}{sec{(\alpha-\beta)} = {\sqrt{6} – \sqrt{2}}}$
f) é a vez da cossecante $\color{blue}{(\alpha-\beta)}$
$\color{navy}{csc{(\alpha-\beta)}=\left({1\over{sen\alpha\cdot cos\beta – sen\beta\cdot cos\alpha}}\right)}$
$csc{(\alpha-\beta)}=\left[{1\over\left({{\sqrt{3}\over2}\cdot{\sqrt{2}\over2}}-{{\sqrt{2}\over2}\cdot{1\over2}}\right)}\right]$=$\left[{1\over\left({{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}\right)}\right]$
$csc{(\alpha-\beta)}=\left[{1\over\left({{\sqrt{6} – \sqrt{2}}\over4}\right)}\right]$=$\left[{4\over{\sqrt{6} -\sqrt{2}}}\right]$
$csc{(\alpha-\beta)}=\left[{4\cdot\left({\sqrt{6}+\sqrt{2}}\right)\over\left({\sqrt{6} – \sqrt{2}}\right)\cdot\left({\sqrt{6}+\sqrt{2}}\right)}\right]$
$csc{(\alpha-\beta)}=\left[{4\cdot\left({\sqrt{6}+\sqrt{2}}\right)\over\left({6 – 2}\right)}\right]$=$\left[{4\cdot\left({\sqrt{6} +\sqrt{2}}\right)\over 4}\right]$
$\color{maroon}{csc{(\alpha-\beta)}={\sqrt{6} +\sqrt{2}}}$
05. Sabe-se que um ângulo tem $sen\gamma={\sqrt{6}\over5}$. Determine: a) $sen{2\gamma}$; b)$cos{2\gamma}$; c)$tg{2\gamma}$; d)$ctg{2\gamma}$
a) Seno do ângulo duplo $\color{green}{sen{2\gamma}}$
Precisamos começar determinando o cosseno do ângulo.
$\color{navy}{sen²\gamma + cos²\gamma = 1}$
$({\sqrt{6}\over 5})² + cos²\gamma = 1$$\Leftrightarrow$${6\over25} + cos²\gamma = 1$
$cos²\gamma = 1 – {6\over{25}}= {{25 -6}\over25}$
$\sqrt{cos²\gamma} = {\sqrt{{19}\over{25}}}$
$\color{blue}{cos\gamma = {\sqrt{19}\over5}}$
$\color{navy}{sen{(2\gamma)}= {2\cdot sen\gamma\cdot cos\gamma}}$
$sen{(2\gamma)}={2\cdot \left({\sqrt{6}\over 5}\right)\cdot\left({\sqrt{19}\over 5}\right)}$
$sen{(2\gamma)}= {2\cdot\left({\sqrt{114}\over{25}}\right)}$
$\color{maroon}{sen{(2\gamma)}= {2\sqrt{114}\over25}}$
b)$cos{(2\gamma)}$
$\color{navy}{cos{(2\gamma)}={cos^2\gamma – sen^2\gamma}}$
$cos{(2\gamma)}={\left({\sqrt{19}\over 5}\right)^2 – \left({\sqrt{6}\over 5}\right)^2}$
$cos{(2\gamma)}={{{19}\over{25}} – {6\over{25}}}={{13}\over{25}}$
$\color{maroon}{cos{(2\gamma)}={{13}\over{25}}}$
c)$\color{green}{tg{(2\gamma)}}$
Comecemos por determinar a $\color{red}{tg\gamma}$ e $\color{red}{ctg\gamma}$
$\color{blue}{tg\gamma = {{sen\gamma}\over {cos\gamma}}}$
$tg\gamma = \left[{({\sqrt{6}\over 5})\over({\sqrt{19}\over 5})}\right]$=$\left[{({\sqrt{6}\over \not{5}})\cdot({\not{5}\over\sqrt{19}})}\right]$
$tg{\gamma}=\left[{{\sqrt{6}\cdot\sqrt{19}}\over{\sqrt{19}\cdot\sqrt{19}}}\right]$= ${\sqrt{114}\over{19}}$
$\color{maroon}{tg\gamma = {\sqrt{114}\over{19}}}$
$\color{blue}{ctg\gamma = {1\over tg\gamma}}$
$ctg\gamma = \left[{1\over{\sqrt{114}\over{19}}}\right]$=$\left[{{19}\over\sqrt{114}}\right]$
$ctg\gamma=\left[{({19}\cdot\sqrt{114})\over({\sqrt{114}\cdot\sqrt{114}})}\right]$=$\left[{({{19}\cdot\sqrt{114}})\over{114}}\right]$
$\color{maroon}{ctg{(\gamma)}={\sqrt{114}\over 6}}$
$\color{navy}{tg{(2\gamma)}= {2\over{ctg\gamma – tg\gamma}}}$
$tg{(2\gamma)}=\left[{2\over{\left({\sqrt{114}\over 6}\right)-\left({\sqrt{114}\over{19}}\right)}}\right]$=$\left[{2\over\left({{{19}\sqrt{114} – 6\sqrt{114}}\over{114}}\right)}\right]$
$tg{(2\gamma)}=\left[{({2\cdot{114}})\over({{113}\cdot\sqrt{114}})}\right]$=$\left[{\left(2\cdot{114}\sqrt{114}\right)\over\left({113\sqrt{\left(114\right)}²}\right)}\right]$
$\color{maroon}{tg{(2\gamma)}= {2\sqrt{114}\over {113}}}$
d)$\color{green}{ctg{(2\gamma)}}$
$\color{blue}{ctg{(2\gamma)}={1\over tg{(2\gamma)}}}$
$ctg{(2\gamma)}=\left[{1\over({2\sqrt{114}\over {113}})}\right]$=$\left[{{113}\sqrt{114}\over{2\sqrt{114}^2}}\right]$
$ctg{(2\gamma)}=\left[{{{113}\sqrt{114}}\over 228}\right]$
$\color{maroon}{ctg{(2\gamma)}={{113}\sqrt{114}\over{228}}}$
Exercícios para treinar
01. Se um triângulo isósceles tem o ângulo oposto à base, medindo $\alpha = 60º$, determine o seno e o cosseno do ângulo resultante da justaposição de dois desses triângulos, como mostra a figura.
02. Sabendo que um ângulo $\beta$ mede mede 30º e o outro mede 45º. Determine a tangente e cotangente da soma desses dois ângulos.
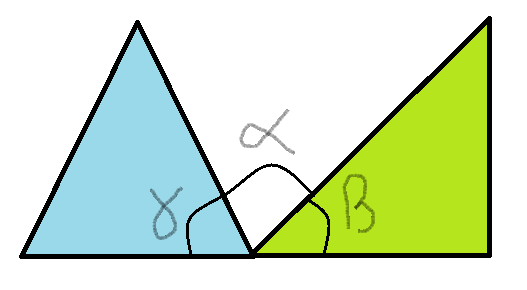
03. Dois triângulos são colocados lado a lado, de modo a fazer coincidir um de seus vértices da base. O primeiro é equilátero e o segundo isósceles, onde o ângulo do vértice superior mede 45º. Determine: a) o seno do ângulo entre os lados dos dois triângulos $\color{red}{\alpha}$; b) o cosseno da soma do ângulo interno do equilátero e o lado do isósceles$\color{red}{(\alpha + \gamma)}$; c) o seno do ângulo formado entre a base do isósceles e o lado do equilátero$\color{red}{(\alpha + \beta)}$.
05. Sendo os ângulos $\color{red}{\alpha = 60º}$ e $\color{red}{\beta = 45º}$, determine: a) $cos{(\alpha – \beta)}$; b)$sen{(\alpha – \beta)}$; c)$tg{(\alpha – \beta)}$.
06. Calcular as restantes razões trigonométricas sabendo que tgα=4/3 e α pertence ao primeiro quadrante($0\lt\alpha\lt90^{0}$.
07. Demostrar as seguintes igualdades trigonométricas:
a)$\left[{{1 – sen\alpha}\over cos\alpha}\right] = \left[{{cos\alpha}\over{1 + sen\alpha}}\right]$;
b) $\left[{{sen\alpha + ctg\alpha}\over{tg\alpha + cosec\alpha}}\right] = cos\alpha$;
c)${tag\alpha + ctg\alpha} = sec\alpha\cdot csec\alpha$;
d)$cos^2\alpha = sen^2\alpha\cdot cos^2\alpha + cos^4\alpha$
08. Faça a demonstração das igualdades trigonométricas:
a)$\color{blue}{2tg x\left({{1 + cos x}over 2}\right)} = sen x\cdot tg x$
b)$\color{blue}{\left({{tg\alpha + tg\beta}\over{ctg\alpha +ctg\beta}}\right) = tg\alpha\cdot tg\beta}$
09. Demonstrar as seguintes igualdades trigonométricas.
a)$\color{blue}{sec^2\alpha + csc^2\alpha = sec^2\alpha\cdot csc^2\alpha}$
b)$\color{blue}{\left({{sen\alpha\cdot cos\alpha}\over{sen^2\alpha -cos^2\alpha}}\right) = sec^2\alpha\ cdot csc^2\alpha}$
c)$\color{blue}{{\left(sec\alpha – tg\alpha\right)^2 }=\left({{1-sen\alpha}\over{1+sen\alpha}}\right)}$
10. Demonstre as seguintes identidades trigonométricas.
a)$\color{blue}{sen\alpha + cos\alpha = \left({{1 + tg\alpha}\over{sec\alpha}}\right)}$
b)$\color{blue}{\left({{cos\alpha + tg\alpha}\over{cos\alpha\cdot tg\alpha}}\right) = ctg\alpha + sec\alpha}$
c)$\color{blue}{\left({{2sen\alpha}\over{tg(2\alpha)}}\right) = cos\alpha – \left({sen²\alpha\over cos\alpha}\right)}$
11. Demonstrar as seguintes igualdades trigonométricas.
a)$\color{blue}{1 + sen\alpha\cdot tg\alpha = \left({{sen\alpha + ctg\alpha}\over{ctg\alpha}}\right)}$
b)$\color{blue}{tg\alpha + ctg\alpha = \left({1\over{sen\alpha\cdot cos\alpha}}\right)}$
c)$\color{blue}{{\left(sen\alpha + cos\alpha\right)^2} +{\left(sen\alpha – cos\alpha\right)^2} = 2}$
12. Calcular as restantes razões trigonométricas sabendo que $ sen\alpha=3/5 $ e $0\lt\alpha\lt90$, isto é pertence ao primeiro quadrante.
13. Calcular as outras razões trigonométricas sabendo que o $cos\alpha=5/13$ e $ \alpha$ pertence ao primeiro quadrante.
14. Calcular as outras razões trigonométricas sabendo que $ tgα=4/3$ e $α$ pertence ao primeiro quadrante.
15. Calcular as demais razões trigonométricas sabendo que o $\color{Green}{ cos\alpha={4\over 5}}$ e $0< α<90^{0}$, isto é, pertence ao primeiro quadrante.
Irá seguir em pouco tempo um post com a resolução de todos esses exercícios para que possas conferir e tirar dúvidas.
Curitiba, 30 de dezembro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

