Plano Cartesiano
O Plano Cartesiano é formado por um par de eixos, preferencialmente ortogonais, que se interceptam em um ponto, denominado origem e ao qual associamos o número $0$ (zero). Um eixo tido geralmente como “horizontal” e o outro “vertical”. O primeiro é denominado eixo das abcissas e o segundo era o eixo das ordenadas.
Cada ponto desse plano pode ser identificado por meio de um par de números, que são medidos sobre os eixos. Os dois números recebem o nome de “par ordenado“. O primeiro é a abcissa ou $x$ e o segundo é a “ordenada” ou $y$. Vamos ver um exemplo de Plano Cartesiano, com alguns pontos identificados pelos pares ordenados.
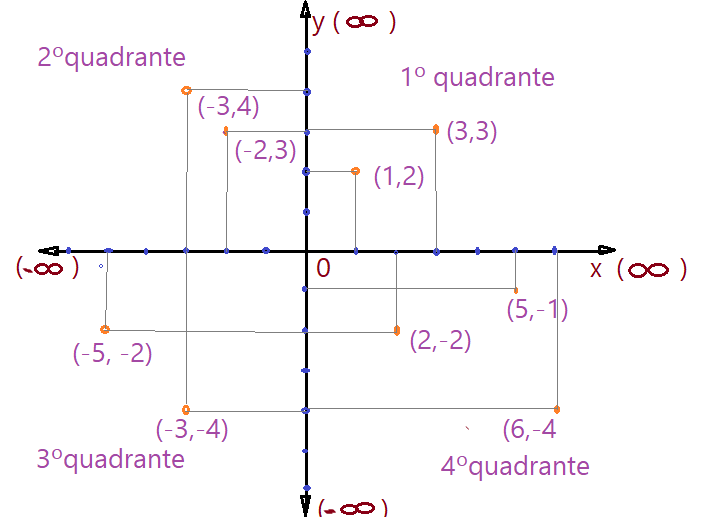
Os eixos dividem o plano em quatro quadrantes. Os pontos do primeiro quadrante são identificados por dois números positivos; no segundo quadrante a abcissa é negativa e a ordenada positiva; no terceiro quadrante os dois números do par ordenado são negativos. Por último, no quarto quadrante a abcissa é positiva e a ordenada é negativa. É convencionado universalmente que o sentido dos quadrantes é anti-horário.
Os pontos situados sobre o eixo das abcissas terão todos o valor $0$ (zero) na ordenada, como por exemplo $(5; 0)$. Já os pontos do eixo das ordenadas terão todos como abcissa o valor $0$ (zero), como por exemplo $(0; -7)$
Para facilitar o entendimento desse assunto, vamos retomar o estudo dos conjuntos. Na ocasião vimos várias operações com conjuntos. Aqui iremos ver mais uma de nominada Produto Cartesiano.
\begin{align}\color{Sepia}{A = \{ 1; 2; 3\}}\end{align}
\begin{align}\color{Sepia}{B = \{1; 3; 5; 7\}}\end{align}
Denominamos produto cartesiano do conjunto A, pelo conjunto B, ao conjunto de pares ordenados (x, y), onde o elemento $x$ pertence ao conjunto A e o elemento $y$ pertence ao conjunto B. Isso pode ser traduzido em símbolos matemáticos da seguinte forma:
\begin{align}\color{NavyBlue}{A\times B = \{(x,y)| x\in A \land y\in B \}}\end{align}
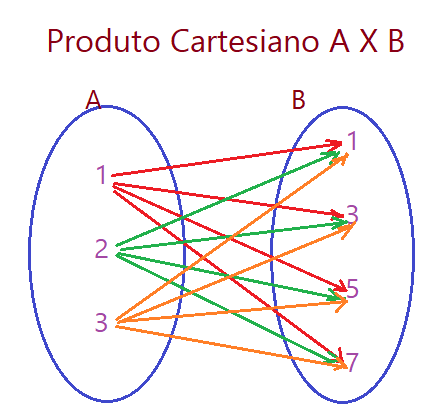
Num Diagrama de Venn teremos esse produto assim representado.
Note que de cada elemento do conjunto A, saem quatro setas dirigidas aos elementos do conjunto B. Isso nos indica que o numero de pares ordenados desse produto cartesiano é igual ao produto do número de elementos de ambos os conjuntos.
$$\color{Brown}{n(A X B) = 3\times 4 = 12}$$
${A X B = \{(1; 1), (1; 3), (1; 5), (1; 7), (2; 1), (2; 3), (2; 5), (2;7), (3; 1), (3; 3), (3; 5), (3; 7)\}}$
Esse assunto é de fundamental importância no desenvolvimento dos programas de informática, especialmente na construção dos chamados Bancos de Dados.
Podemos também fazer o produto cartesiano invertido, isto é, trocando a ordem dos conjuntos. Será:
\begin{align}{B X A = \{(1; 1),(1; 2),(1; 3),(3;1),(3;2),(3;3),(5;1),(5;2),(5;3),(7;1),(7;2),(7;3)\}}\end{align}
Se contarmos os pares, também iremos encontrar o número $12$, uma vez que o número de elementos de cada conjunto apenas inverteu a ordem, isto é aplicamos a propriedade comutativa.
Podemos estabelecer o produto cartesiano ${A X A}$, o que equivale a ${A^2}$, e ${B X B}$ equivalendo a ${B^2}$.
Neste caso o número de pares será:
$n(A X A) = 3\times 3 = 3^2 = 9$
${A^2 = \{(1;1),(1;2),(1;3),(2;1),(2;2),(2;3),(3;1),(3;2),(3;3)\}}$
$n{B^2} = 4\times 4 = 4^2 = 16$
${B^2 = \{(1;1),(1;3),(1;5),(1;7),(3;1),(3;3),(3;5),(3;7),(5;1),(5;3),(5;5),(5;7),(7;1),(7;3),(7;5),(7;7)\}}$
No estudo das funções, usaremos sempre conjuntos numéricos, que podem ser limitados, conforme a situação em análise.
Temos o conjunto dos números naturais, representado pela letra N, que inclui todos os números inteiros, inclusive o $0$ (zero).
${N = \{0, 1, 2, 3, 4, 5, 6, 7, …+\infty\}}$
Temos o conjunto dos números naturais não nulos, onde fica excluído o $0$ (zero).
${N_{\neq 0} = \{1, 2, 3, 4, 5, 6, 7, … +\infty\}}$
Temos os números inteiros relativos, representado pela letra $Z$. Começa no menos infinito e vai até o mais infinito.
${Z = \{-\infty, …, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … , +\infty\}}$
Temos o conjunto dos números inteiros relativos positivos, que coincide com os naturais e o representamos por $Z_{+}$
${Z_{+} = \{0, 1, 2, 3, 4, 5, 6, 7, 8, … , + \infty\}}$
O conjunto dos números inteiros relativos negativos, representado por $Z_{-}$.
${Z_{-} =\{-\infty, … , -5, -4, -3, -2, -2, -1, 0\}}$
Conjunto dos números racionais, simbolizado por $Q$.
${Q = \{-\infty, … , – \frac{13}{3}, … , -\frac{10}{3}, -3, … , -\frac{5}{2}, …, -1, …-\frac{2}{3}, …, 0, … \frac{1}{2}, …, \frac{7}{3},…, 3, …, \frac{11}{3}, …, +\infty\}}$
Observamos que o conjunto numérico fica cada vez mais amplo. Tanto que para escrever o mesmo, recorremos aos intervalos de reticências entre alguns elementos, uma vez que fica impossível relacionar todos.
Temos ainda o conjunto dos números Reais, no qual reunimos todos os demais conjuntos em um só. Representado por $R$. Pode ser tomado só o lado positivo, o lado negativo ou o conjunto inteiro, excluindo o $0$ (zero).
${R_{+}}$$\Rightarrow$ Números reais positivos, inclusive o zero.
${R_{-}}$$\Rightarrow$ Números reais negativos, incluindo o zero.
${R_{\neq 0}}$$\Rightarrow$ Números reais, excluído o zero.
${R}$$\Rightarrow$ Conjunto dos números reais.
Chegará o momento em que iremos nos deparar com uma nova ampliação do conjunto dos números. Será o momento dos Números imaginários. Reunido aos números Reais formarão o conjunto dos Números complexos.
Vamos exercitar um pouco.
01. Dados os conjuntos ${A= \{3; 5\}}$ e ${B =\{2; 5; 8\}}$, represente-os em um Diagrama de Venn e faça um gráfico de flechas indicando o produto cartesiano ${A X B}$.
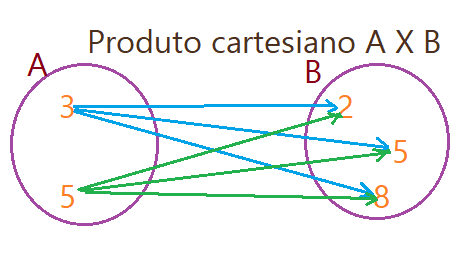
O conjunto dos pares ordenados resultante desse produto cartesiano é o que segue.
${A X B = \{(3;2), (3;5), (3;8), (5;2), (5;5), (5;8)\}}$
${n(A X B) = 2\times 3 = 6\,pares}$
02. Use os conjuntos do exercício 01 e faça o produto cartesiano ${B X A}$. Represente um diagrama de flechas num Diagrama de Venn.
${B X A = \{(2;3), (2;5), (5;3), (5;5), (8;3), (8;5)\}}$
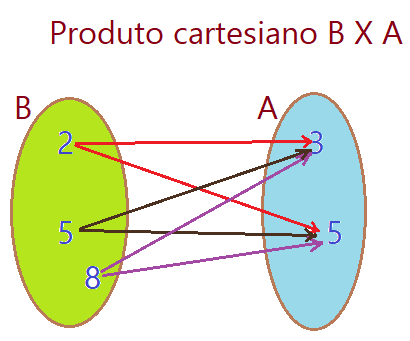
${n(B XA) = 3\times 2 = 6\,pares}$
03. Dado o produto cartesiano entre os conjuntos $M$ e $N$. Seus elementos são ${M = \{-3, 0, 4, 7\}}$ e ${N = \{-1, 1, 3\}}$. Determine os pares ordenados do produto e represente-os num plano cartesiano.
${M X N =\{(-3; -1),(-3; 1),(-3; 3),(0;-1),(0; 1),(0; 3),(4; -1),(4; 1),(4;3),(7; -1),(7; 1),(7;3)\}}$
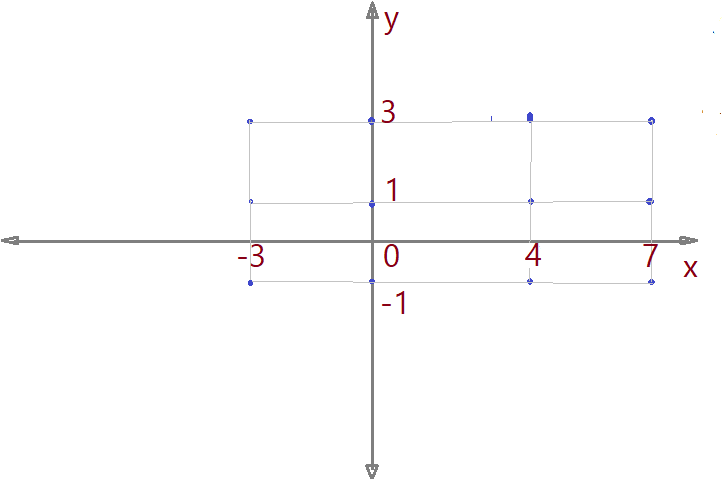
Notamos que os pontos representados ficam alinhados segundo as ordenadas e também segundo as abcissas.
04. Se tomarmos os elementos do conjunto $N$, símbolo dos números naturais, quantos pares ordenados poderemos formar fazendo o produto cartesiano $N^2$?
05. No produto cartesiano de dois conjuntos, pode haver um elemento que seja excluído do produto?
06. Seja o conjunto ${G =\{(x \in Z_{+}| 10\lt x \le 15\}}$. Faça o produto cartesiano ${G X G}$. Escreva o conjunto dos pares ordenados do produto e faça um gráfico de flechas, bem como represente no plano cartesiano.
Havendo dúvidas, peça esclarecimento por um dos canais abaixo listados.
Curitiba, 06 de julho de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

