Matemática – Conjuntos. Relações e funções

Relação de um conjunto em outro.

Dados dois conjuntos $A = {2; 5; 8}$ e $B = {1; 3; 6; 10}$ , denominamos Relação de $r : A \to B$ ao conjunto de pares ordenados ${(x, y) | x \in A \land y \in B}$ . A relação é um sub-conjunto do produto cartesiano dos dois conjuntos.

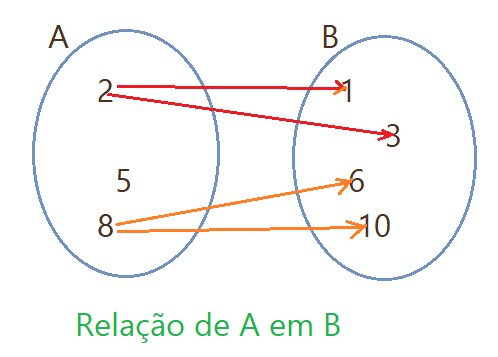
Note que nem todos os elementos do conjunto $A$ fazem parte da relação com o conjunto $B$ e ao mesmo elemento de $A$ podem corresponder mais de um elemento do conjunto $B$ .

$R_{1} = {(2; 1), (2; 3), (8; 6), (8; 10)}$

Uma outra relação entre os mesmos conjuntos poderia ser:

$R_{2} = {(2; 1), (5; 3), (5; 6)}$

O segundo elemento de cada par ordenado é denominado Imagem do primeiro. O conjunto $A$ , dito conjunto de partida, habitualmente recebe a denominação Domínio da relação e o conjunto $B$ , conjunto de chegada, é o Contra Domínio da relação. Podemos inverter a ordem dos conjuntos, passando o $A$ a ser contra domínio e o $B$ o Domínio. Os diagramas de Venn dos conjuntos Domínio e Contra Domínio, com as setas unindo os elementos do primeiro aos elementos do segundo recebe o nome Diagrama de Flechas.

Função

Uma relação de um conjunto $A$ em outro $B$ , onde cada elemento do Domínio, tem uma e somente uma imagem no Contra Domínio, recebe o nome de função.

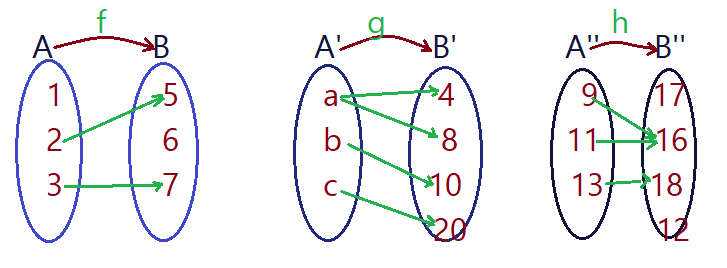
Nos diagramas de Venn da figura, a relação f não é função, pois há um elemento do conjunto $A$ sem a correspondente imagem no conjunto $B$ .

A relação g não é função pois há um elemento do conjunto $A^{'}$ ao qual correspondem duas imagens no conjunto $B^{'}$ .

A relação h é uma função pois a cada elemento do conjunto $A ”$ corresponde uma e somente uma imagem no conjunto $B ”$ . Observe que o conjunto que contém os elementos imagens pode conter elementos que não são imagem de nenhum elemento de $A ”$ . Também vemos que um mesmo elemento pode ser imagem de mais de um elemento do conjunto domínio.

O primeiro conjunto, no caso $A ”$ , é o domínio da função. O conjunto $B ”$ contém o conjunto imagem e recebe a denominação de contra domínio.

$D_{h} = A ” = {9, 11, 13}$

$C D_{h} = B ” = {12, 16, 17, 18}$

$I_{h} = {16, 18}$

$I_{h} \subset B ”$

$B ” \supset I_{h}$

Classificação das funções

Função sobrejetora

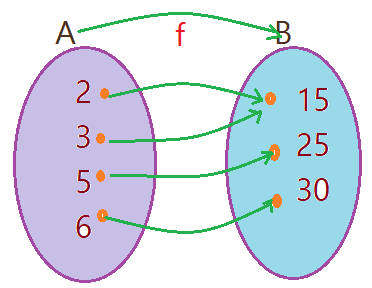
É a função em que todos os elementos do Contra Domínio são imagem de pelo menos um elemento do Domínio, isto é, não sobram elementos no contra domínio.

Função injetora

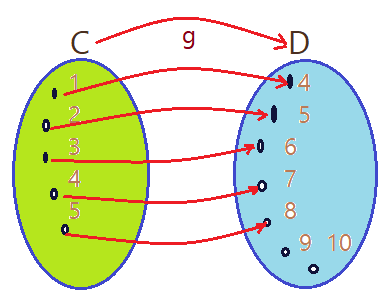
A função é injetora se cada elemento do Domínio tem uma imagem distinta no Contra domínio.

Função bijetora

É bijetora a função que preenche os requisitos de ser sobrejetora e injetora ao mesmo tempo. Em outras palavras não sobram elementos do Contra Domínio e nenhum elemento é imagem de dois ou mais elementos do Domínio.

No estudo das funções algébricas via de regra o Domínio e o Contra Domínio são o mesmo conjunto numérico.

Por exemplo:

$f : R \to R$

$f : N \to N$

$f : Z \to Z$

$f : Q \to Q$

Exercitemos um pouco.

01. Sendo $A = {1, 2}$ e $B = {1, 3, 4}$ , determine:

a) $A X B = {(1, 1); (1, 3); (1, 4); (2, 1); (2, 3); (2, 4)}$

b) A relação formada pelos pares ordenados em que o $1^{0}$ elemento é menor que o $2^{0}$ elemento:

$r_{1} = {(1, 3); (1, 4); (2, 3); (2, 4)}$

c)A relação formada pelos pares ordenados em que o $1^{0}$ é maior que o $2^{0}$ elemento;

$r_{2} = {(2, 1)}$

d)A relação formada pelos pares ordenados em que o $1^{0}$ elemento é igual ao $2^{0}$ elemento;

$r_{3} = {(1, 1)}$

e)A relação formada pelos pares ordenados em que o $1^{0}$ elemento é o dobro do $2^{0}$ elemento.

$r_{4} = {(2, 1)}$

f) A relação formada pelos pares ordenados em que o $2^{0}$ é o dobro do $1^{0}$ elemento;

$r_{5} = {(2, 4)}$

02. Qual é a relação formada pelos pares ordenados do produto cartesiano de $A = {1, 2, 3}$ por $B = {2, 4, 5}$ , tal que o segundo elemento de cada par seja o dobro do primeiro elemento?

$r = {(1, 2); (2, 4)}$

03. Dados os conjuntos $A = {1, 3, 5}$ e $B = {2, 3}$ , determinemos:

a) $A X B = {(1, 2); (1, 3); (3, 2); (3, 3); (5, 3); (5, 3)}$

b) $B X A = {(2, 1); (2, 3); (2, 5); (3, 1); (3, 2); (3, 5)}$

c) $A^{2} = A X A = {(1, 1); (1, 3); (1, 5); (3, 1); (3, 3); (3, 5); (5, 1); (5, 3), (5, 5)}$

d) $B^{2} = B X B = {(2, 2); (2, 3); (3, 2); (3, 3)}$

04. Dados os conjuntos $A = {1, 3, 5, 7}$ e $B = {3, 9, 15, 20}$ , a relação $R : A \to B$ de modo que $(x, y) \in (A X B) | b = 3 a$ , será formada pelos pares ordenados ${(1, 3); (3, 9), (5, 15)}$ .

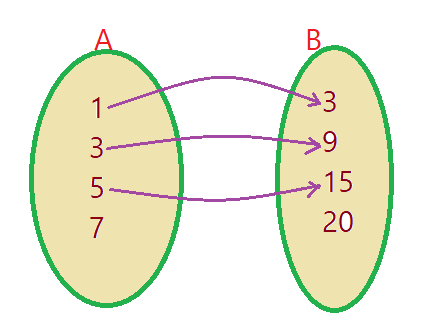
Relação de $A \to B$ representada em diagrama de Venn

Representando num diagrama de flechas, ficamos com:

05. Dados os conjuntos $A = {1, 2, 3, 4}$ e $B = {4, 5, 6, 7}$ . A relação mostrada no Diagrama de flechas a seguir, define uma função $f : A \to B$ para a qual $(x, y) \in (A X B) | x \in A \land y \in B$ .

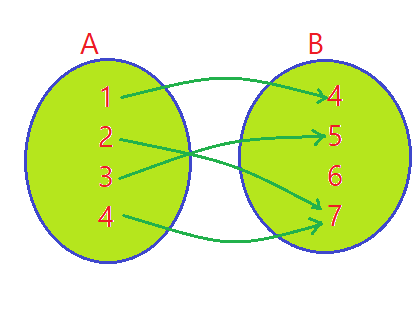
Nesta função temos:

Domínio: $D_{f} = {1, 2, 3, 4}$
Contra domínio: $C D_{f} = {4, 5, 6, 7}$
Imagem: $I_{f} = {4, 5, 7}$
$f : (1) = (4)$
$f : (2) = (7)$
$f : (3) = (5)$
$f : (4) = (7)$

Na expressão $f : (1) = (4)$ , lê-se “função de 1 é igual a 4”. O 4 é imagem de 1.

Exercícios para resolver

01. Dados os conjuntos $A = {3, 5, 7}$ e $B = {3, 9, 15, 35}$ , determine os produtos cartesianos:

a) $A X B$ ; b) $B X A$ ; c) $A^{2}$ ; d) $B^{2}$

02. Dados os conjuntos $A = {- 2, - 1, 0, 1}$ e $B = {0, 1, 2, 3}$ ,

determine:

a) a relação $R_{1} = {(x, y) \in A X B | y = x^{2} - 1}$

b) a relação $R_{2} = {(x, y) \in A^{2} | b = a^{2}}$

c) a relação $R_{3} = {(x, y) \in B X A | y = x^{2}}$

d) determine o domínio e a imagem de cada relação.

03. Dados os conjuntos $A = {3, 5, 7}$ e $B = {3, 9, 15, 35}$ , determine:

a) a relação $R : A \to B$ , de modo que $R = {(x, y) \in (A X B) | \frac{y}{x} \in N}$ . Construa o diagrama de flechas da relação.

b) o domínio e a imagem de $R$

04. Dados os conjuntos $A = {1, 2, 7, 10}$ e $B = {2, 5, 33, 50, 101}$

a) determine a relação $R_{1} : A \to B$ , tal que $R_{1} = {(x, y) \in (A X B) | x \land y}$ são números primos. Faça o diagrama de flechas.

b) determine a relação $R_{2} : A \to B$ , tal que $R_{2} = {x, y) | y = x^{2} + 1}$ . Faça o diagrama de flechas.

c) a relação $R_{1}$ é uma função? Explique. Se for determine a imagem dessa função.

d) a relação $R_{2}$ é uma função? Explique. Se for determine a imagem dessa função.

05. Dados os conjuntos $A = {3, 8, 15, 24}$ e $B = {2, 3, 4, 5}$

a) determine a relação $R_{1} : A \to B$ , tal que $R_{1} = {(x, y) \in (| b = \sqrt{a + 1}}$ . Diagrama de flechas

b) determine a relação $R_{2} : B \to A$ , tal que $R_{2} = {(x, y) | y = x - 1}$ . Faça o diagrama de flechas.

c) A relação $R_{1}$ é uma função? Explique. Sendo função, determine a imagem da mesma.

d) A relação $R_{2}$ é uma função? Explique. Se for determine a imagem dessa função.

06. – Considere três funções f, g e h, tais que:
A função f atribui a cada pessoa do mundo, a sua idade.
A função g atribui a cada país, a sua capital
A função h atribui a cada número natural, o seu dobro

Podemos afirmar que, das funções dadas, são injetoras:
a) f, g e h
b) f e h
c) g e h
d) apenas h
e) nenhuma delas.

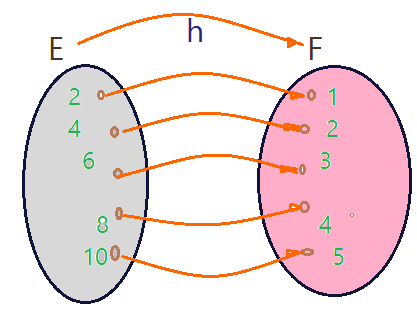
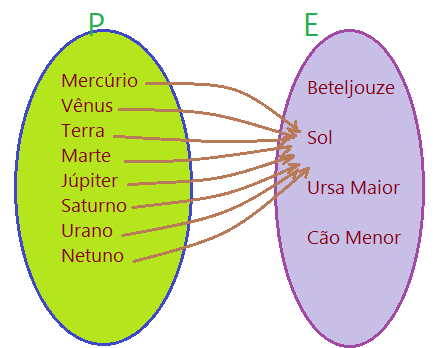
07. Observe o diagrama de flechas abaixo, onde temos o conjunto P formado pelos nomes dos planetas de nosso sistema solar e no conjunto E estrelas e constelações do Universo. O gráfico representa uma função ou é apenas uma relação? Se for função qual é sua classificação?

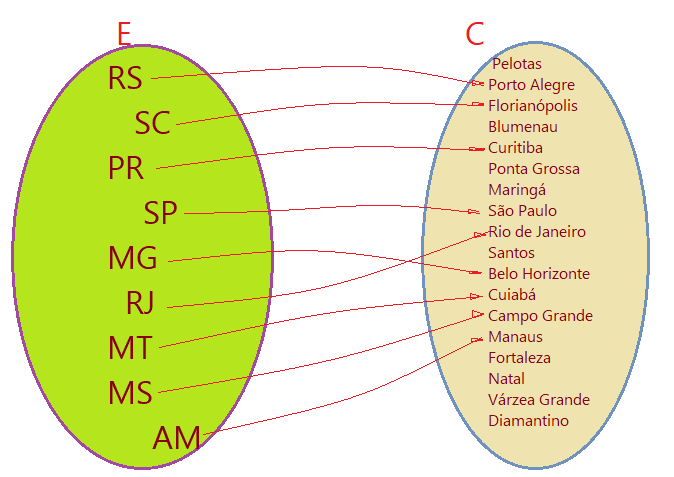
08. O diagrama de flechas a seguir representa os principais estados do Brasil no conjunto Domínio e os nomes de cidades brasileiras. Os estados estão ligados às suas respectivas capitais. O diagrama representa uma função ou não? Se for função, qual é sua classificação?