Conjuntos numéricos – Produto cartesiano

Produto cartesiano!

Que bicho é esse?

Chamamos produto cartesiano de dois conjuntos numéricos A e B, ao conjunto de pares ordenados $\color{maroon}{(x; y)}$, onde $\color{maroon}{ x\in A} $ e $\color{maroon}{ y\in B}$. 

Simbólicamente fica

• $\bbox[5px,border:2px solid olive]{\color{maroon}{ A X B =\{{(x;y)} | x \in A \wedge y \in B\}}}$. Lê-se:“A cartesiano B é igual aos pares (x;y), tais que x pertence a A e y pertence a B”.

Podemos inverter a ordem:

• $\bbox[5px,border:2px solid olive]{\color{maroon}{B X A = \{{(x;y)} | x\in B \wedge y \in A\}}}$. Lemos: “B cartesiano A, é igual aos pares (x;y), tais que x pertence a B e y pertence a A”.

Vejamos como fica isso na prática. Sejam os conjuntos:

• \[\bbox[5px,border:2px solid olive]{\color{maroon}{ A =\{1; 2; 3\}}}\]
• \[\bbox[5px,border:2px solid olive]{\color{maroon}{ B = \{1; 3; 5; 7\}}}\]

Temos que combinar cada um dos elementos do conjunto$\color{navy}{A}$, com todos os elementos do conjunto $\color{navy}{B}$, formando os pares.  Teremos no resultado um total de $\color{olive}{n(A)\cdot n(B)}$ pares. Isso nos mostra, que nesse caso teremos $\color{olive}{ 3\cdot 4 = 12}$ pares. Isso permite conferir se no processo não esquecemos de nenhum número.

• \[\bbox[5px,border:3px solid olive]{\color{maroon}{A X B =\{(1; 1),  (1; 3), (1; 5), (1; 7), (2; 1), (2; 3), (2; 5), (2; 7), (3; 1), (3; 3), (3; 5), (3; 7)\}}}\]

Se fizermos o inverso, ocorrerá a troca de todos as posições nos pares. Vejamos:

• \[\bbox[5px,border:3px solid olive]{\color{maroon}{ B X A = \{(1; 1), (1; 2), (1; 3), (3; 1), (3; 2), (3; 3), (5; 1), (5; 2), (5; 3), (7; 1), (7; 2), (7; 3)\}}}\]

Note que o número de pares permanece o mesmo, mas a ordem em que os números aparecem é invertida. Isso só não fica evidente, nos pares em que os valores de${ x}$ e ${y}$ coincidem.

Há uma outra situação possível em se tratando de produto cartesiano. Assim como podemos multiplicar, na forma comum, um número por ele mesmo, podemos fazer o produto cartesiano de um conjunto por ele mesmo. Por exemplo $\color{navy}{A X A}$, lê-se: A cartesiano A.

Seja o conjunto $\color{olive}{A = \{0; 2; 4; 6\}} $. O produto cartesiano por ele mesmo terá $\color{olive}{4\cdot 4}$ pares e ficará:

• \[\bbox[5px,border:3px solid olive]{\color{maroon}{A X A =\{(0;0),(0;2),(0;4),(0;6),(2;0),(2;2),(2;4),(2;6),(4;0),(4;2),(4;4),(4;6),\\(6;0),(6;2),(6;4),(6;6)\}}}\]

O interessante dessa questão, é que podemos ter um produto cartesiano de infinitos pares, dentro do conjunto dos números. Vai depender do que for indicado como $\color{olive}{Conjunto}$ $\color{olive}{Universo}$. Isso é particularmente importante no estudo das funções que virá logo adiante. Desse modo poderemos ter o produto cartesiano no conjunto dos Naturais, Inteiros Relativos, Racionais, Reais e Complexos.

• \[\bbox[5px,border:2px solid olive]{\mathbf{\color{maroon}{N X N = \{(x;y) |x\in N \wedge y \in N \}}}}\]
• \[\bbox[5px,border:2px solid olive]{\mathbf{\color{maroon}{ Z X Z = \{(x;y) |x \in Z \wedge y \in Z \}}}}\]
• \[\bbox[5px,border:2px solid olive]{\mathbf{\color{maroon}{Q X Q = \{(x;y)|x \in Q \wedge y \in Q \}}}}\]
• \[\bbox[5px,border:2px solid olive]{\mathbf{\color{maroon}{R X R = \{(x;y) | x \in R \wedge y \in R\}}}}\]
• \[\bbox[5px,border:2px solid olive]{\mathbf{\color{maroon}{ C X C =\{(x;y) |x \in C \wedge y \in C \}}}}\]
• O produto cartesiano de cada conjunto numérico terá um número infinito de pares ordenados, que poderão ser identificados em um plano${X0Y}$.

Plano cartesiano

É um plano dividido por um par de eixos $\color{navy}{X}$ e $\color{navy}{Y}$, ortogonais (90º). Cada par ordenado obtido no produto cartesiano, corresponde a um ponto desse plano. Em geral, o eixo $\color{maroon}{X}$ é colocado na horizontal e o $\color{maroon}{Y}$ na vertical, imaginando o plano posto frontalmente aos nossos olhos. O ponto de intersecção dos eixos tem como par ordenado a ele associado $\color{olive}{(0;0)}$. Os valores positivos de $\color{navy}{X}$ ficam situados à direita de $\color{olive}{0}$ e os negativos a esquerda. Para $\color{olive}{Y}$ positivo, os pontos ficam acima do $\color{olive}{0}$ e os negativos abaixo. Isso nos mostra que o plano fica dividido em quatro quadrantes. O primeiro quadrante, corresponde aos valores positivos de $\color{olive}{(X;Y)}$, o segundo quadrante tem os pontos identificados por valores negativos de $\color{olive}{X}$ e positivos de $\color{olive}{Y}$; o terceiro quadrante, tem os valores de ambas as coordenadas negativas e o quarto quadrante, corresponde aos pontos com os valores de $\color{olive}{X}$ positivos e os valores de $\color{olive}{Y}$ negativos.

Abcissas

Denominamos abcissas os valores medidos sobre o eixo $\color{maroon}{X}$.

Ordenadas

Os valores medidos sobre o eixo $\color{maroon}{Y}$ recebem o nome de ordenadas.

Este plano fica assim determinado:

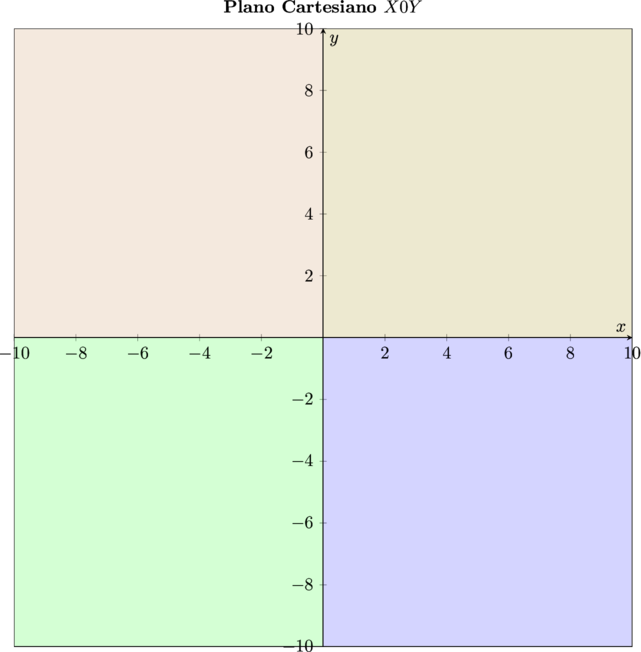
Vamos representar os pontos do produto cartesiano, exemplificado acima.

• \[\bbox[5px,border:3px solid olive]{\color{maroon}{A X B =\{(1; 1),  (1; 3), (1; 5), (1; 7), (2; 1), (2; 3), (2; 5), (2; 7), (3; 1), (3; 3), (3; 5), (3; 7)\}}}\]

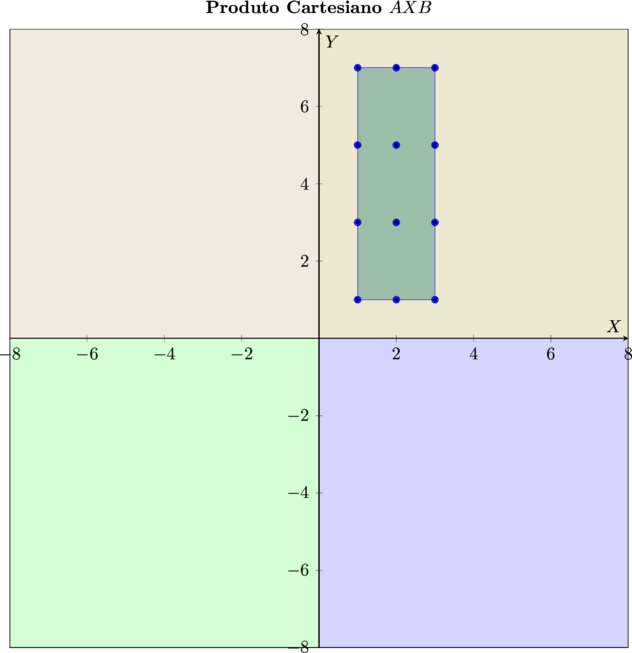
• Obs.: Note que os pontos desse produto cartesiano estão todos colocados no primeiro quadrante, pois os números são todos positivos. O ponto de intersecção dos dois eixos corresponde ao par ordenado $\color{maroon}{(0,0)}$. Ele não está escrito, pois iria haver superposição dos dois números , causando congestionamento ou dificultando a visualização.

Vejamos como fica o outro produto, com a ordem invertida.

• \[\bbox[5px,border:3px solid olive]{\color{maroon}{ B X A = \{(1; 1), (1; 2), (1; 3), (3; 1), (3; 2), (3; 3), (5; 1), (5; 2), (5; 3), (7; 1), (7; 2), (7; 3)\}}}\]

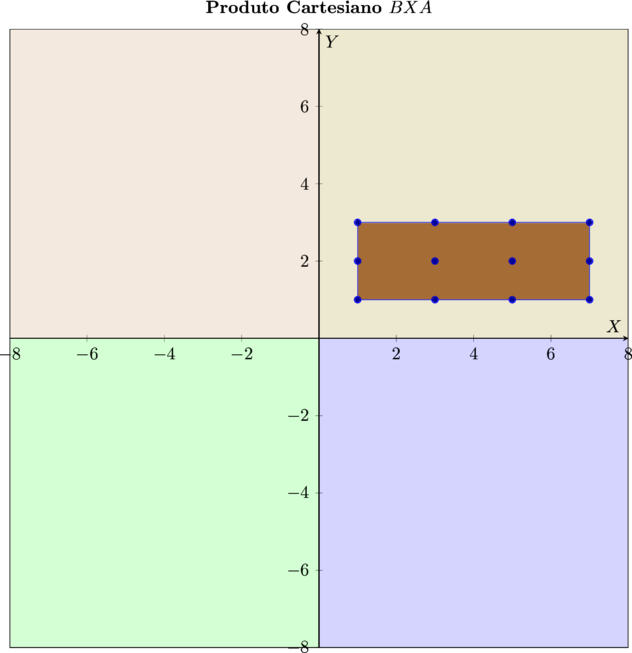
Sejam os conjuntos

• $\bbox[5px,border:2px solid olive]{\color{navy}{M = \{-3; -1; 0; 2\}}}$
• $\bbox[5px,border:2px solid olive]{\color{navy}{N =\{-2; 0; 2\}}}$.

Façamos o produto cartesiano desses conjuntos e representemos no plano cartesiano.

• \[\bbox[5px,border:2px solid olive]{\color{maroon}{ M X N = \{(-3, -2) (-3, 0) (-3, 2) (-1,-2) (-1, 0) (-1, 2) (0, -2) (0,0) (0, 2) (2, -2) (2, 0) (2, 2)\}}}\]

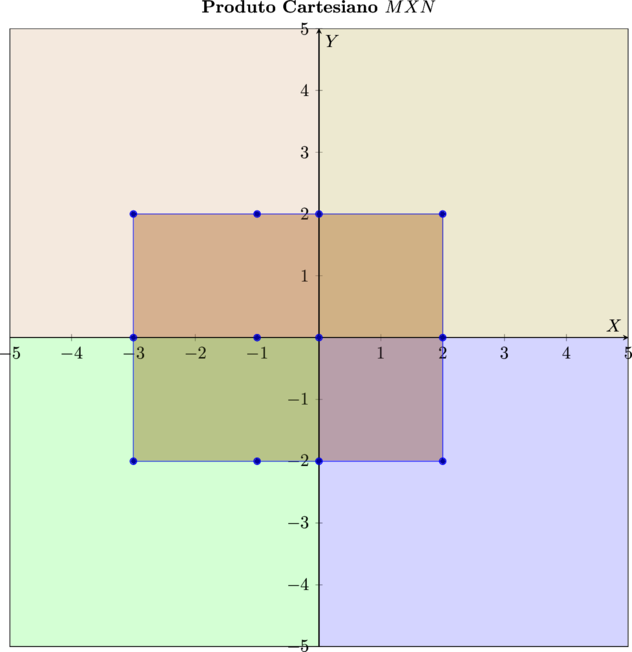
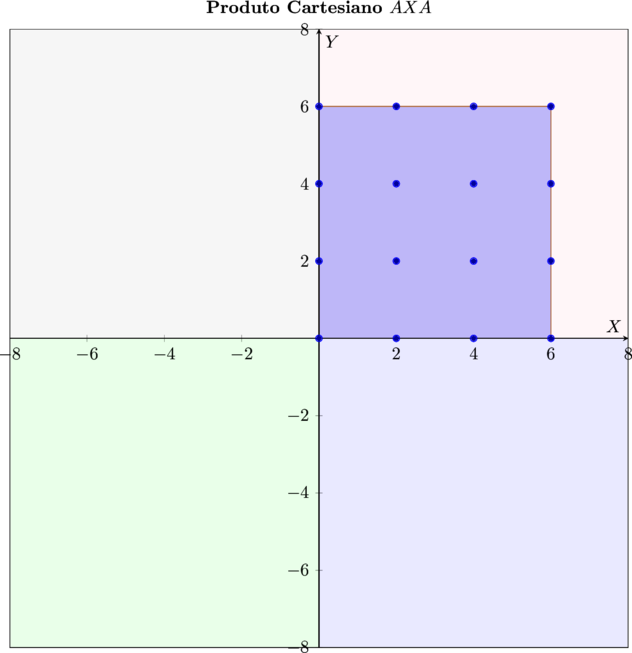
Vamos à representação no plano, do produto cartesiano do conjunto $\color{navy}{A}$ por ele mesmo.

• \[\bbox[5px,border:3px solid olive]{\color{maroon}{A X A =\{(0;0),(0;2),(0;4),(0;6),(2;0),(2;2),(2;4),(2;6),(4;0),(4;2),(4;4),(4;6),\\(6;0),(6;2),(6;4),(6;6)\}}}\]

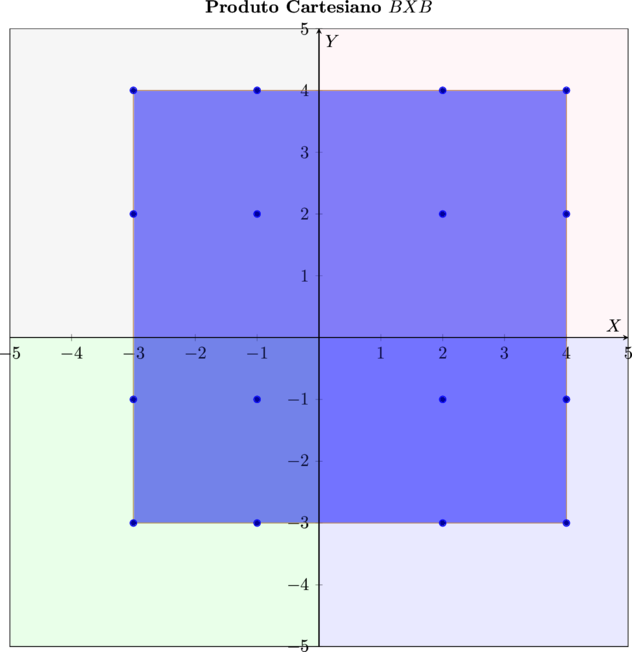
Vamos a mais um exemplo. Seja o conjunto $\color{navy}{B = \{-3, -1, 2, 4\}}$ e o produto cartesiano

• \[\bbox[5px,border:2px solid aqua]{\color{maroon}{BXB = \{(-3, -3) (-3, -1) (-3, 2) (-3, 4) (-1, -3) (-1, -1) (-1, 2) (-1, 4) (2, -3) (2, -1)\\ (2, 2) (2, 4) (4, -3) (4, -1) (4, 2) (4, 4)\}}}\]

Exercitando!

Para adquirir habilibade em produtos cartesianos e sua representação gráfica, vamos fazer os exercícios que seguem.

Sejam os conjuntos

• $\color{navy}{A = \{-6, 0, 3\}}$
• $\color{navy}{B = \{-2, 1, 5, 6\}}$
• $\color{navy}{C = \{0, 2, 4, 5\}}$
• $\color{navy}{D =\{-2, 0, 3\}}$

• Faça os produtos cartesianos a seguir e represente cada um deles em um plano cartesiano.
• $\color{maroon}{A X B}$
• $\color{maroon}{A X C}$
• $\color{maroon}{C X D}$
• $\color{maroon}{B X C}$
• $\color{maroon}{A X D}$
• $\color{maroon}{B X D}$
• $\color{maroon}{A X A}$
• $\color{maroon}{D X D}$
• $\color{maroon}{C X A}$
• $\color{maroon}{D X B}$

Em caso de dúvida sobre a realização desses exercícios, faça contato por meio de um dos canais informados abaixo.

Curitiba, 27 de junho de 2016. Revisado e republicado em 07 de outubro de 2019.

Décio Adams

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadam.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular: (41) 99805-0732