Mais um pouco de Polígonos
Já temos uma noção inicial de triângulos. Podemos dar mais um passo em frente. Vamos estudar os quadriláteros. Os quadriláteros, como diz o nome, são formados por quatro lados. O quadrilátero regular é o quadrado, ou seja, é formado por quatro lados congruentes e tem quatro ângulos internos que medem ${90}^0$ cada. Os lados são paralelos dois a dois.
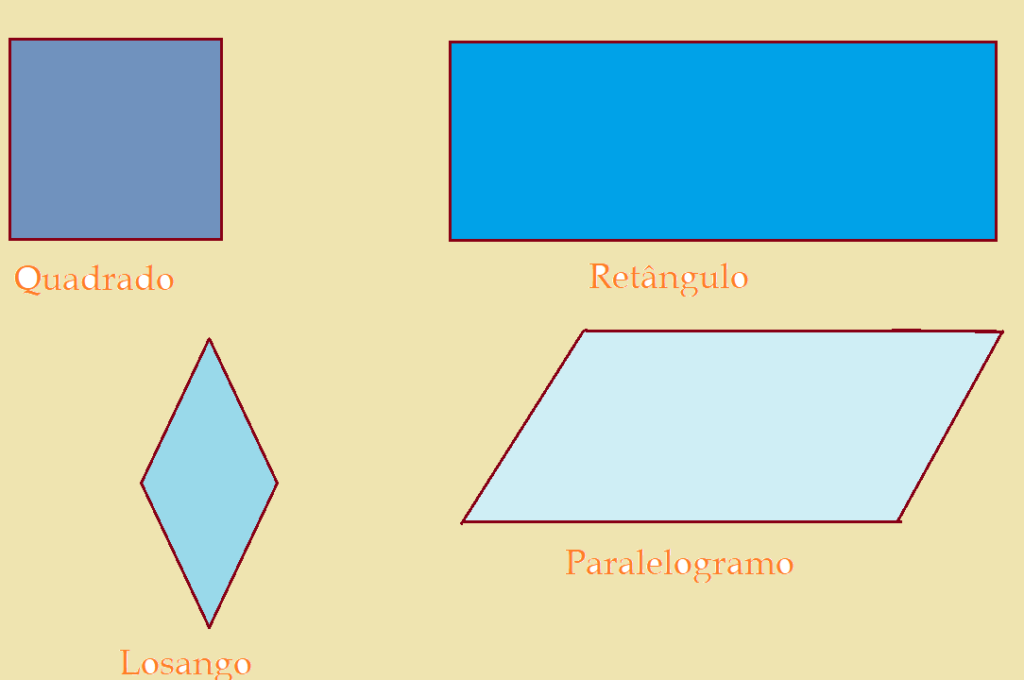
Existe uma denominação genérica para os polígonos de quatro lados paralelos. São os paralelogramos. O quadrado é um exemplo de paralelogramo, mas existem vários outros.
Paralelogramo: – figura geométrica de quatro lados, paralelos dois a dois.
Quadrado: – é um paralelogramo que tem os quatro lados congruentes, formando ângulos retos, isto é, iguais a ${90}^0$.
Losango: – é um paralelo gramo que tem os quatro lados congruentes e paralelos dois a dois, porém apenas os ângulos opostos são necessariamente congruentes.
Retângulo: – é o paralelogramo que tem os lados congruentes e paralelos dois a dois, formando ângulos retos (${90}^{0}$).
O que é uma diagonal?
Diagonal é o segmento de reta que une dois vértices não consecutivos de um polígono.
Dessa forma, os paralelogramos possuem apenas um par de diagonais que se interceptam no centro da figura. As diagonais dividem o paralelogramo em quatro triângulos. Nos quadrados e losangos os triângulos são congruentes, pois as diagonais formam entre si ângulos retos. Nos retângulos e demais paralelogramos as diagonais formam ângulos suplementares e os triângulos são congruentes dois a dois.
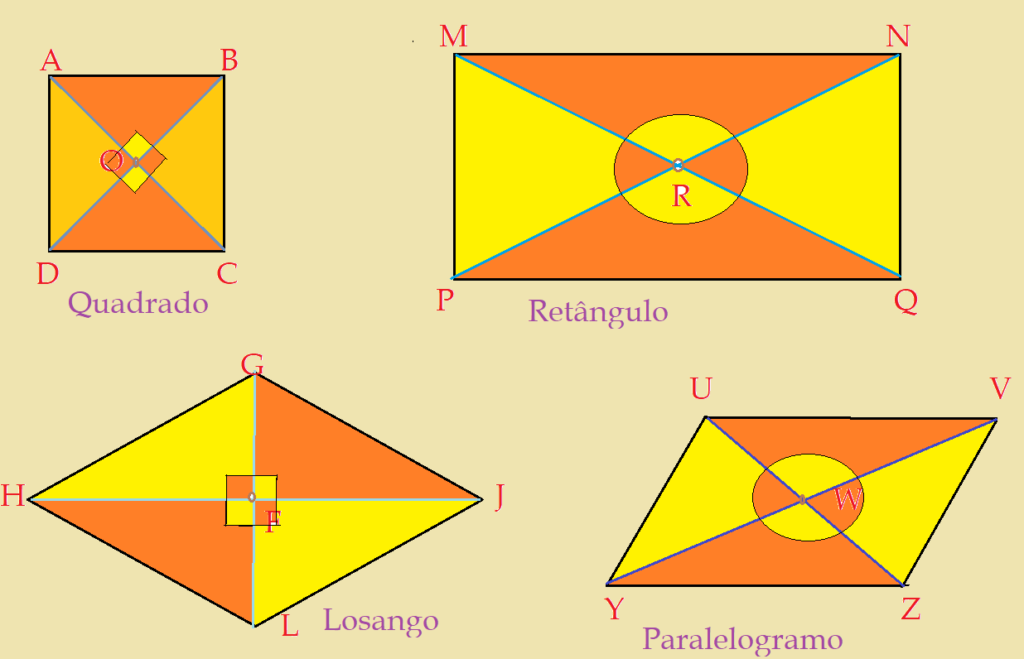
Em todas essas situações é possível aplicar o Teorema de Pitágoras para solucionar questões relativas aos lados e ângulos dos paralelogramos.
Aplicando o que foi visto em relação aos ângulos formados por paralelas e uma transversal conseguiremos mostrar que a soma dos ângulos internos de qualquer paralelogramo é igual a ${360}^{0}$.
Área de um quadrado
Para constatar que a área de um quadrado é igual à medida de seu lado, elevada ao quadrado, basta construir um quadrado e dividir com linhas horizontais e verticais. Notamos que o número de linhas de quadrinhos é igual ao de colunas, ou seja, basta multiplicar o lado por ele mesmo.
$S = {l}\cdot{l} = {l^2}$
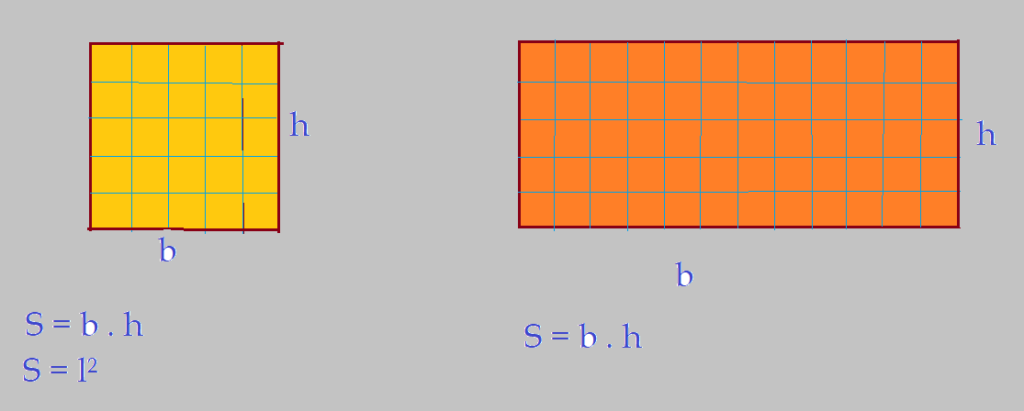
Área do retângulo
Também aqui fazemos a divisão em linhas e colunas, multiplicando os resultados. Isso nos dá que:
$S = {b}\cdot {h}$
Retângulo áureo
Um retângulo que tem comprimento $a$ e largura $b$ de modo que $\frac{a}{b} = \frac{b}{a-b} = \Phi$ é denominado retângulo áureo.
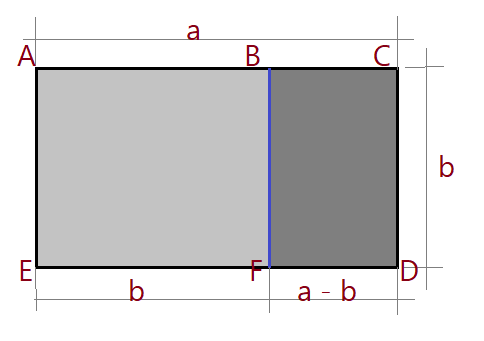
Isso permite construir um segundo retângulo, de modo que a razão entre suas áreas seja igual à razão áurea.
$\frac{a\times b}{b\times b} = \frac{b\times b}{b\times(a – b)} = \Phi$
$\Phi = \frac{b^{2} + b(a – b)}{b^{2}}$$\Leftrightarrow$$\Phi = \frac{b^{2}}{b^{2}} + \frac{b(a-b)}{b^{2}}$
Simplificando os fatores comuns ficamos com:
$\Phi = 1 + \frac{a – b}{b}$$\Leftrightarrow$$\Phi = 1 + \frac{1}{\Phi}$
${\Phi}^{2} = \Phi + 1$$\Leftrightarrow$${\Phi}^{2} – \Phi – 1 = 0$
Assim provamos ser um retângulo áureo. A solução dessa equação do segundo grau é:
$\Phi = \frac{1 +\sqrt{5}}{2} = 1,618$
Área do losango
Na figura podemos observar que se completamos um retângulo, usando as medidas das diagonais do losango, a área do mesmo será igual ao dobro do losango. Isto permite que façamos o cálculo da área, multiplicando as diagonais e dividindo o resultado por $2$
$ S = {{{d}\cdot{D}}\over{2}}$
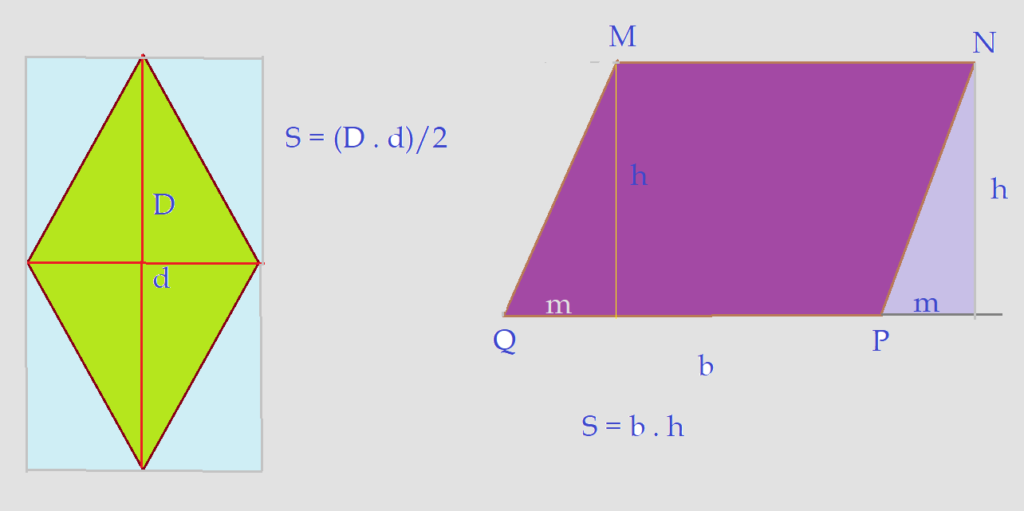
$S = {b}\cdot{h}$
Área de um triângulo
Deixei essa área para esse momento, pois fica mais fácil entender a fórmula a partir da área dos paralelogramos. Vejamos a figura.
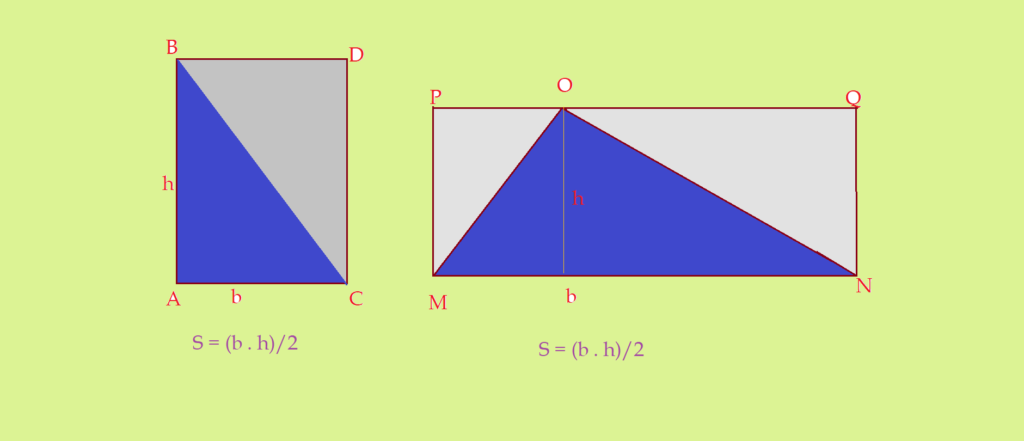
A área do triângulo, seja ele qual for, é calculada pelo produto da base pela altura, dividido por dois.
$S = {{{b}\cdot {h}}\over{2}}$
Apótema do quadrado.
No quadrado fica muito mais fácil determinar o apótema. Ele é um segmento que une o centro geométrico, intersecção das diagonais, ao meio de qualquer um dos lados. Isto nos leva a concluir que:
$a = {l\over 2}$
Raio da circunferência circunscrita
O raio da circunferência circunscrita, é o segmento que une o centro geométrico a qualquer um dos vértices ou seja, tem a medida da metade da diagonal.
$d² = l² + l²$$\Leftrightarrow$ $d = \sqrt{2\cdot{l²}}$
$d = l\sqrt{2}$
Sendo $R = {d\over2}$ $\Leftrightarrow$$R = {{l\sqrt{2}}\over{2}}$
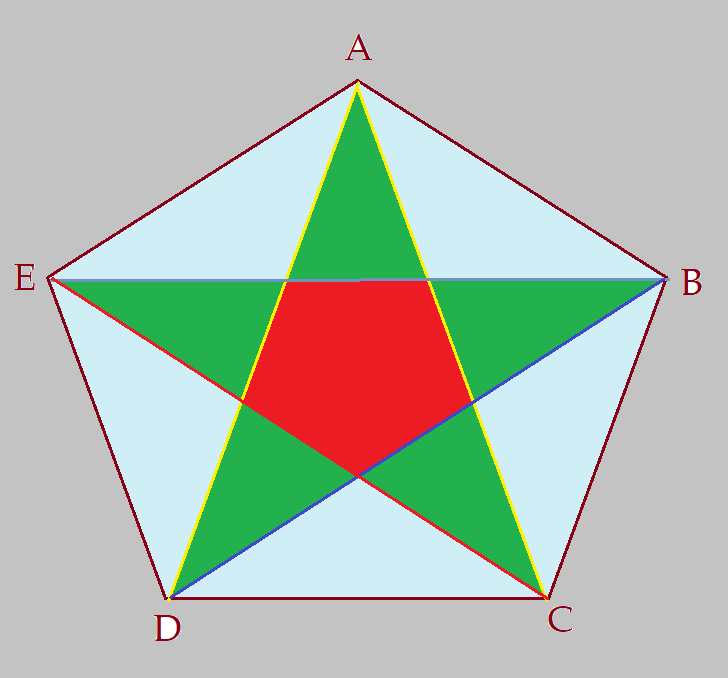
Pentágono
O nome dessa figura geométrica vem do grego penta = cinco. Portanto um polígono de cinco lados é um pentágono. Para ser um pentágono regular, é necessário que seus lados e seus ângulos internos sejam congruentes.
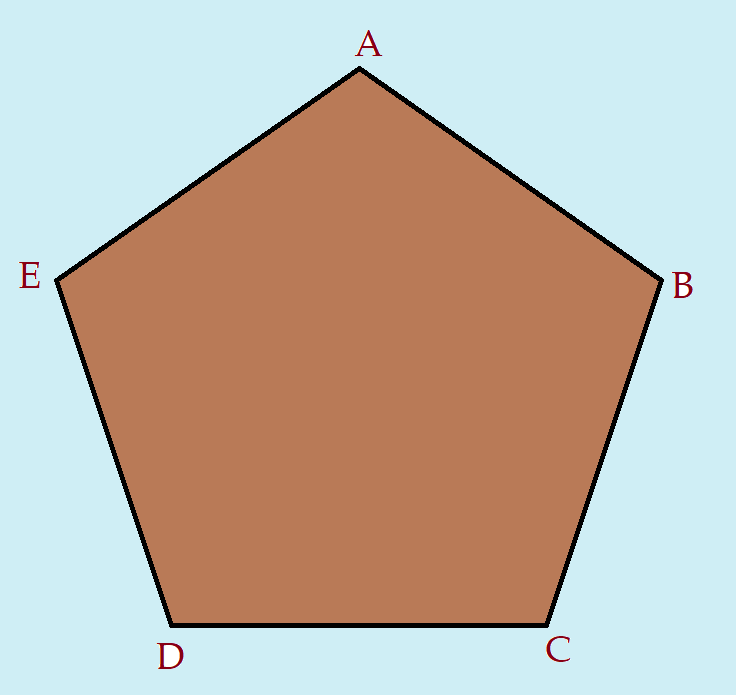
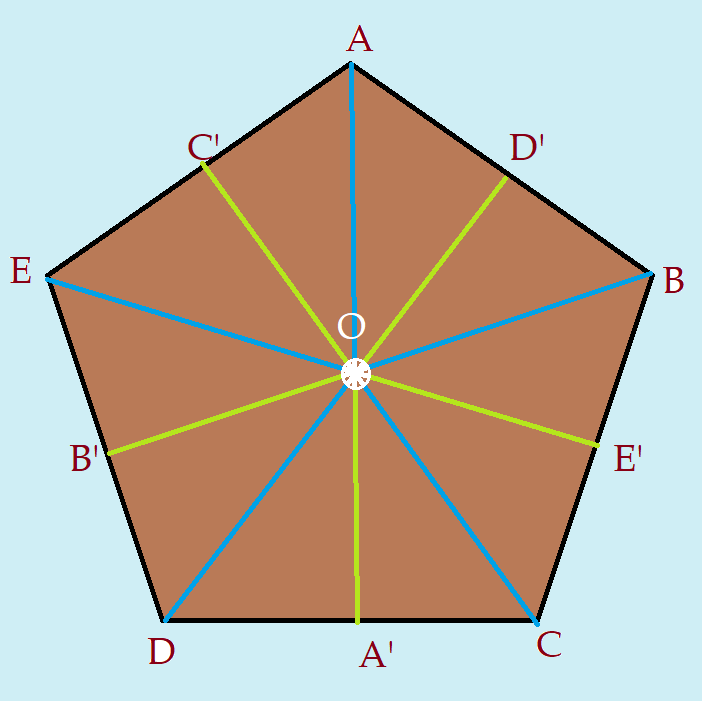
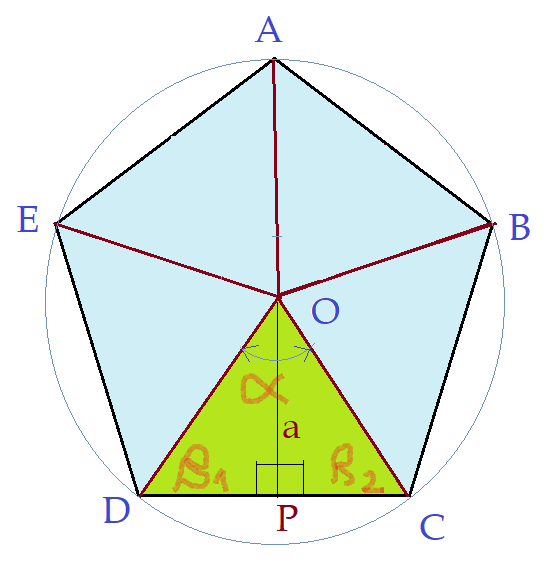
O ângulo central $\alpha$, é obtido pela divisão da volta completa em 5(cinco) partes iguais.
$\alpha = {{{360}^{0}}\over{4}} = {72}^{0}$
O segmento $\overline{OP} = a$ é denominado apótema do pentágono e é o raio da circunferência inscrita na figura.
O triângulo $\Delta{(OCDO)}$ é um triângulo isósceles. Isso nos leva a concluir que os dois ângulos formados pelo lado $\overline{CD}$; os lados $\overline{OC}$ e $\overline{OD}$, são congruentes $\beta_{1} = \beta_{2} = \beta$. Como os ângulos internos do triângulo somam ${180}^0$, podemos concluir que:
$\beta_{1} + \beta_{2} + {72}^0 = {180}^{0}$
$\beta_{1} + \beta_{2} = {180}^{0} – {72}^{0}$
$2{\beta} = {108}^{0}$$\Leftrightarrow$$\beta = {{{108}^{0}}\over{2}} = {54}^{0}$
Apótema – é o segmento $\overline{OP} = a$ e que corresponde à altura do triângulo $\Delta{(OCDO)}$. Este segmento divide o lado $\overline{CD}$ em dois, permitindo aplicar o Teorema de Pitágoras no $\Delta{(OMDO)}$, onde o segmento $\overline{OD} = R$ é a hipotenusa, o apótema $a$ e a metade do lado $\overline{CD} = m$ são os catetos. Temos então:
${R}^2 = a^2 + m^2$ $\Leftrightarrow$ $ a^2 = R^2 – m^2$
$\sqrt{a^2} = \sqrt{{R^2 – {[R\cdot{cos (54)^0]}}^2}}$
$a = \sqrt{{R² – {[R\cdot{cos(54)^0}]}²}}$
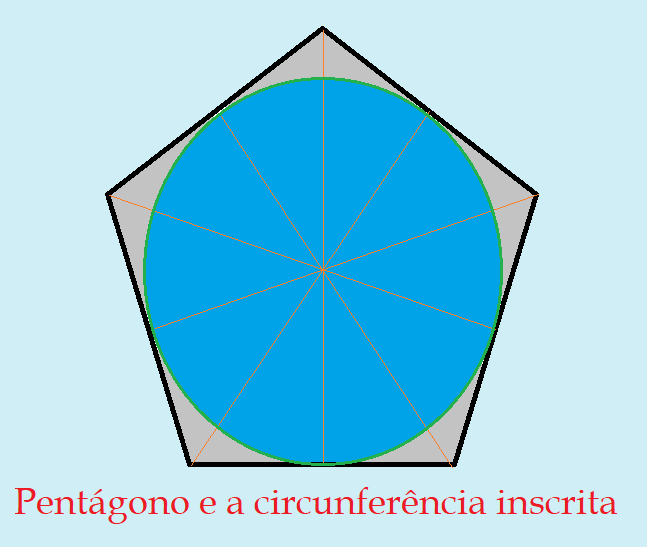
Medida do ângulo interno
Cada ângulo interno é formado por dois ângulos dos triângulos em que dividimos o pentágono. Vimos que cada ângulo mede $54^0$. Logo, o ângulo interno do pentágono mede
$\hat{i} = 2\cdot{54^0} = 108^{0}$
Sendo cinco ângulos internos $S_{5} = 5\cdot {108^0} = 540^0$
Exercitar é preciso!
- Se um lote de esquina tem as medidas indicadas na figura a seguir, determine a área das duas partes que formam o L e a sua soma.
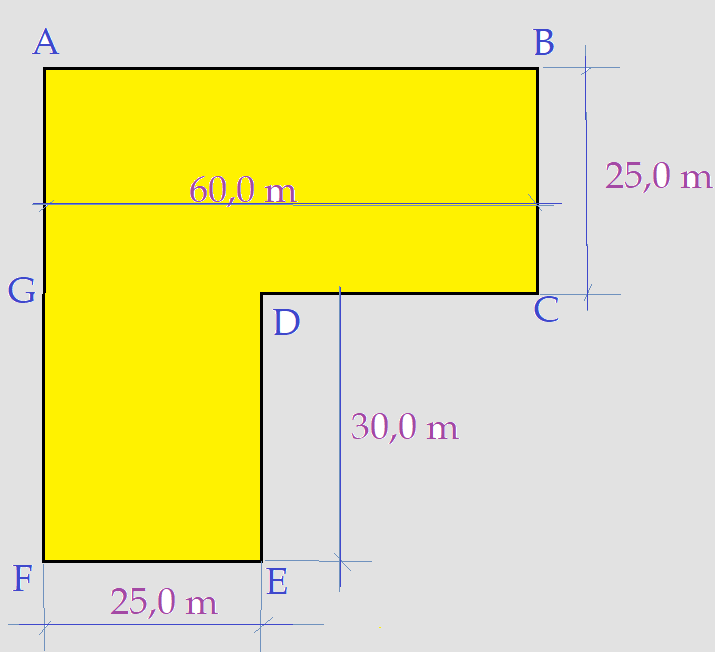
Basta aplicarmos a forma de cálculo da área de um retângulo e teremos as duas áreas. Fazemos a soma e obtemos a área total do lote.
a) parte 1 $(60,0) m X (25,0)m $
$S_{1} = {b}\cdot {l}$ $\Leftrightarrow$ $ S_{1} = {(60,0)}\cdot{(25,0)} = 1500,0 m²$
b) parte 2 $(25,0) m X (30,0) m$
$S_{2} = {c}\cdot{h}$ $\Leftrightarrow$ $S_{2} = {(25,0)}\cdot{(30,0)} = 750,0 m²$
c) total $ S_{1} + S_{2} = S$
$S = 1500,0 + 750,0 = 2250,0 m²$
O total do lote é de 2250,0 m².
2. Numa quadra onde uma das ruas não é perpendicular à outra, o primeiro terreno ficou assim configurado.
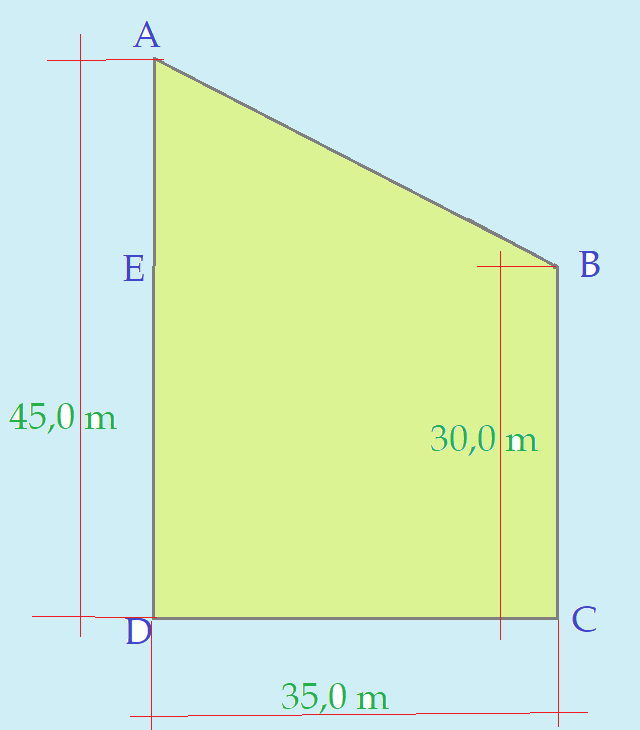
Podemos identificar o triângulo $\Delta{(ABEA)}$ e o retângulo ${(BCDEB)}$.
Área do triângulo
$b = \overline{BE} = 35,0 m$
$h = \overline{AE} = {45,0 – 30,0}m$
$S_{1} = {{b\cdot h}\over 2}$$\Leftrightarrow$ $S_{1} ={{{35,0}\cdot{15,0}}\over{2}}$
$S_{1} = {{525,0}\over2} = 262,5 m²$
Área do retângulo
$b =\overline{BC} = 30,0 m$
$h = \overline{CD} = 35,0 m$
$S_{2} = b\cdot h$ $\Leftrightarrow$ $S_{2} = {30,0}\cdot{35,0} = 1050,0 m²$
Soma das áreas
$ S = S_{1} + S_{2}$ $\Leftrightarrow$$ S = 262,5 + 1050,0 = 1312,5 m²$
3. Um triângulo retângulo tem área $S = 30,0 cm²$ e sua hipotenusa mede $a = 13,0 cm$. Determine as medidas de seus catetos.
$S = {b\cdot c}\over{2} = 30,0 cm²$$\Leftrightarrow$ $b = {{60,0}\over{c}}$ (I)
$a² = b² + c² $ $\Leftrightarrow$ ${(13,0)}^2 = {\left({60,0}\over{c}\right)^2} + c^2 $
$169,0 = {{3600,0}\over{c²}}+ c²$$\Leftrightarrow$${169,0\cdot c²} = 3600 + c^4$
Fazendo $c² = x$, teremos $c^4 = x²$
$169,0 x = 3600,0 + x²$$\Leftrightarrow$ $x² – 169,0 x + 3600,0 = 0$
Usando a fórmula $ x = {{-b \pm\sqrt{b² – 4\cdot a\cdot c}}\over{2\cdot a}}$
$x = {{-(-169,0)\pm\sqrt{{169,0}^2 – 4\cdot 1\cdot 3600}}\over{2\cdot 1}}$
$ x = {{169,0\pm\sqrt{28561 – 14400}}\over{2}}$
$x = {{169,0\pm\sqrt{14161}}\over{2}}$$\Leftrightarrow$$x={{169,0\pm{119}}\over{2}}$
$x_{1} = {{169,0 + 119,0}\over{2}} = {288,0\over 2} = 144,0$
$S_{2} = {{169,0 – 119,0}\over{2}} = {{50.0}\over {2}} = 25,0$
Substituindo em $c² = x$
$c² = 144,0$$\Leftrightarrow$$\sqrt{c²} = \sqrt{144.0}$
$c = 12,0 cm$
$c² = 25$$\Leftrightarrow$$c =\sqrt{25,0} = 5,0 cm$
Os catetos do triângulo medem respectivamente $5,0 cm$ e $12,0 cm$
Agora é sua vez.
- Um poste de iluminação, projeta uma sombra de 8,0 m, quando o sol está em determinada inclinação. Se a altura do poste é de 6,0 m, determine a distância entre a extremidade superior do poste e a extremidade da sombra projetada.
- Um losango tem a diagonal menor medindo $d = 16,0 cm$. Se sua área é de ${S = 240,0 cm²$ qual é a medida de sua diagonal menor?
- Um retângulo tem a diagonal medindo $ d = 20,0 cm$ e sua largura é de $l = 12,0 cm$. Determine a medida do comprimento e a área do retângulo.
- Um triângulo retângulo tem hipotenusa igual a $a = 25,0 m$ e um de seus catetos mede $b = 20,0 m$. Determine a medida do outro cateto e também a área do triângulo.
- Um quadrado está inscrito em uma circunferência de raio ${R = 5,0 m$. Determine o raio da circunferência que se inscreve exatamente no interior desse quadrado, a medida do lado desse quadrado e a área do mesmo.
- Um retângulo mede $ b = 6,0 cm$ e $h = 10,0 cm$. Determine a medida de sua diagonal, o raio da circunferência que se inscreve totalmente no interior do mesmo, a área desse retângulo.
- Um paralelo gramo tem comprimento de $c = 25,0 cm$. Sua área é de $S = 300,0 cm²$. Calcule sua largura e a medida dos lados menores.
- O apótema de um quadrado mede $a = 6,0 m$. Determine a medida de seu lado, a medida das diagonais e sua área.
- Um losango tem as diagonais medindo $d=12,0 cm$ e $D=16,0 cm$. Determine a área desse losango, a medida de seu lado e depois calcule o raio da circunferência que se pode inscrever no seu interior. (Desafio)
Se tiver dúvidas, venha depressa pedir auxilio por um dos canais abaixo.
Curitiba, 30 de outubro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

