Raízes possíveis.
Lembrando da potenciação, vamos ter em mente que, qualquer potência de expoente par, resulta em um número positivo. Já os expoentes ímpares, resultam em números com o mesmo sinal da base. Pelo fato de a radiciação ser a operação inversa da potenciação, vamos ter situações em que a raiz não é possível, isso é não existe. Vamos analisar alguns exemplos.
1. $\color{Brown}{\begin{align}{\sqrt [2] {9}} & = {\sqrt[2]{3^2}} & = 3\end{align}} $
2. $\color{Blue}{\begin{align}{\sqrt[3] {8}} & ={\sqrt[3] {2^3}} & = 2\end{align}}$
3. $\color{Brown}{\begin{align}{\sqrt[3]{- 8}} & ={\sqrt[3]{ (-2)^3}} & = – 2\end{align}}$
4.$\color{Blue}{\begin{align}{\sqrt[5]{- 32}} & = {\sqrt[5] {(- 2)^5}} & = -2\end{align}}$
5. $\color{Brown}{\begin{align}{\sqrt[4]{ – 16 }}& = {\not\exists} & = Ø\end{align}}$
Por que o exemplo (5) não tem resposta? É que nenhum número elevado a uma potência de expoente par, dará como resultado um número negativo. Então representamos o resultado por um conjunto vazio ou o símbolo de “não existe”.
Nos exemplos usamos só números de pequeno valor, pois o objetivo é explicar como funciona. Essa conclusão é válida em qualquer caso. Para o radicando negativo, só existe resposta se o índice do radical for ímpar.
As demais regras são idênticas à radiciação de números naturais.
Nota: Apenas para chamar atenção, vamos informar aqui que, o caso das raízes de índice par que não existem, essa limitação ocorre no âmbito do conjunto dos números reais. Na continuação dos estudos, chegará o momento de conhecer os números imaginários e complexos. É um conjunto numérico ampliado, onde será possível extrair a raiz de índice par de um número negativo. Mas isso é conteúdo a ser visto mais adiante, no momento oportuno.
Para exercitar o assunto visto acima. Determine as raízes dos números contidos nos radicais abaixo.
a)$\color{Sepia}{\sqrt[2]{+121} = ? }$
b)$\color{Sepia}{\sqrt[3]{-729} = ?}$
c)$\color{Sepia}{\sqrt[5]{+32}=?}$
d)$\color{Sepia}{\sqrt[5]{-243}=?}$
e)$\color{Sepia}{\sqrt[4]{- 81} = ?}$
f)$\color{Sepia}{\sqrt[2]{+1296} =?}$
g)$\color{Sepia}{\sqrt[3]{-216} = ?}$
h)$\color{Sepia}{\sqrt[5]{-3125} =?}$
Simplificar radicais
Quando não for possível extrair a raiz exata, isto é o radicando não é uma potência de um número inteiro, podemos fazer a simplificação, desde que possamos decompô-lo em um produto, onde haja um ou mais fatores que tenham raízes exatas, ficando os demais dentro do radical. Vejamos por exemplo.
$$\color{Orchid}{\sqrt[3]{+432} = ?}$$
Decompondo o radicando + 432 em seus fatores primos, resulta ${2⁴}\cdot{3³}$ e podemos fazer a substituição.
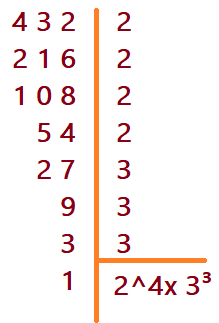
$$\color{Indigo}{\sqrt[3]{2⁴\cdot 3³}}$$
Notemos que os expoentes dos fatores dentro do símbolo de “raiz” apresentam valores $4$ e $3$. O primeiro é par e não é múltiplo do índice da raiz que é 3. Mas podemos decompor a potência, em multiplicação de potências de mesma base, onde uma delas seja múltiplo do índice da raiz.
${2³\cdot 2\cdot 3³}$
Colocando essa forma dentro do radical, vamos poder simplificar os fatores com expoente divisível pelo índice, ficando no interior apenas o fator com expoente diferente. Os fatores simplificados, são multiplicados pelo radical remanescente.
$\begin{align}\sqrt[3]{2³\cdot 2\cdot 3³} \\=\sqrt[3]{2^3}\sqrt[3]{2}\sqrt[3]{3^3} &= 2\cdot 3\cdot\sqrt[3]{2} = 6\sqrt[3]{2}\end{align}$
$$\color{BrickRed}{\sqrt[3]{432} = 6\sqrt[3]{2}}$$
Outro exemplo
${\sqrt[4]{+900} = ?} $
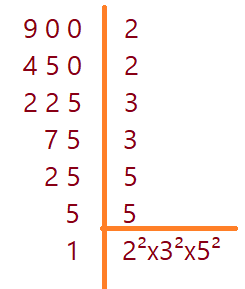
Ao decompormos o radicando 900 em seus fatores primos, iremos encontrar
${2²\cdot 3²\cdot 5²} $
Colocamos sob o sinal de raiz e vamos verificar. Todos os expoentes são menores do que o índice da raiz, mas todos são pares e o índice é divisível por eles. Isso nos permite dividir o índice pelo fator comum 2 e teremos uma raiz simplificada. Assim:
$\begin{align}{\sqrt[4]{2²\cdot 3²\cdot 5²}} & = {\sqrt[2]{2\cdot 3\cdot 5}} ={\sqrt[2] {30}}\end{align}$
$$\color{BrickRed}{\sqrt[4]{900} = \sqrt[2]{30}}$$
Esse radical atingiu sua forma mais simples e certamente será mais fácil de manusear em cálculos posteriores se eles existirem no problema que esteja sendo resolvido. Sempre que possível, é conveniente proceder às simplificações em qualquer problema ou expressão, pois isso facilita a continuidade de outros cálculos que sejam necessários. Quanto menores os números e menos operações tivermos que realizar, menos oportunidades de cometer erros irão aparecer.
Vamos exercitar um pouco? Simplifique as raízes apresentadas a seguir.
a)$\color{Orchid}{\sqrt[3]{+16200} = ? }$
b)$\color{Orchid}{\sqrt[5]{ – 3456} = ?}$
c)$\color{Orchid}{\sqrt{+ 3456} = ? }$
d)$\color{Orchid}\sqrt[4]{3⁶\cdot 5⁸\cdot 7⁴} =?$
e)$\color{Orchid}{\sqrt[3]{432} = ?}$
f)$\color{Orchid}{\sqrt[5]{7776} = ?}$
g)$\color{Orchid}{\sqrt[3]{54\cdot {16}} = ?}$
Obs.: Em caso de dúvida, me procure por um dos meios informados abaixo.
Curitiba, 07 de maio de 2016. Melhorado e republicado em 21 de dezembro de 2017.
Décio Adams, IWA
Fone: (41) 3019-4760 – Celular e WhatsApp: (41) 99805-0732
E-mail:
Facebook (perfil): www.facebook.com/decio.adams
Facebook (Fan Page): www.facebook.com/livros.decioadams
Facebook(Fan Page): www.facebook. com/decioadams.matfisonline
Blog: http://decioadams.netspa.com.br

