Polígonos de múltiplos lados.
Em postagens anteriores, abordamos todos os tipos de polígonos, até os de sete lados.
O que notamos é que os polígonos que apresentam cálculos em si mais complexos são os com número ímpar de lados, especialmente os que correspondem aos números primos. Mas podemos notar que há alguns passos que se tornam repetitivos. As dificuldades ficam por conta das aproximações decimais, dos ângulos com medidas não exatas e as razões trigonométricas.
Vejamos o caso do Octógono.
A divisão do círculo em oito partes, resulta em um ângulo central de $\alpha = 45^{0}$. Os lados formarão ângulos internos que suplementam o ângulo central.
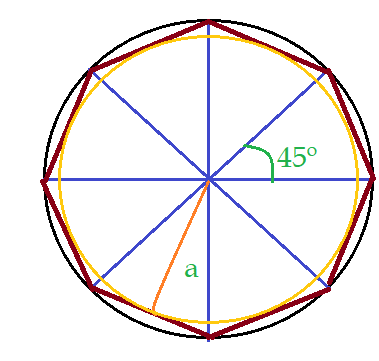
$\hat{i}_{8} = 180^{0} – 45^{0} = 135^{0}$
Desse modo: $\hat{S}_{i_{8}}= {8\cdot{135}^{0}} = 1080^{0}$
Da mesma forma podemos calcular o número de diagonais da figura:
$D_{8} ={{\left({n – 3}\right)\cdot n}\over 2}$
$D_{8} ={{\left({8 – 3}\right)\cdot 8}\over 2} = {{5\cdot 8}\over 2} = 20\, diagonais$
O lado dos triângulos, ou seja o raio da circunferência circunscrita, será sempre à distância do centro a qualquer um dos vértices.
O apótema, calcularemos dividindo um dos triângulos centrais em dois triângulos retângulos, como fizemos nos casos anteriores.
Os demais cálculos serão uma repetição da mesma forma.
O eneágono: – polígono de nove lados, nos fornecerá um ângulo central de $\alpha = 40^{0}$
Embora seja um número ímpar de lados, não apresenta ângulos que resultam em divisões aproximadas.
$\hat{i}_{9} = {180}^{0} – 40^{0}= {140}^{0}$.
Soma dos ângulos internos:
$S_{i_{9}}= {{{180}^{0}\cdot 9} – {360}^{0}} = 1260^{0}$
Número de diagonais:
$D_{9} ={{\left({n – 3}\right)\cdot n}\over 2}$
$D_{9} ={{\left({9 – 3}\right)\cdot 9}\over 2} = 27$
E se for um Decágono?
Terá 10(dez) lados. Os ângulos centrais dos triângulos irão medir $\alpha = 36^{0}$
Os ângulos internos medirão:
$\hat{i}_{10} = 180^{0} -36^{0} = 144^{0}$
$S_{i_{10}} = {{{180}^{0}\cdot {10}} – {360}^{0}} = {1440}^{0}$
Número de diagonais:
$D_{10}={{\left({n – 3}\right)\cdot n}\over 2}$
$D_{10}={{\left({10 – 3}\right)\cdot{10}}\over 2}$
$D_{10} ={{7\cdot{10}}\over 2} = 35$
Exercitando
01. Determine o apótema, a área de cada triângulo e a área total de um eneágono regular inscrito em uma circunferência de raio $R = 12,0\, cm$.
Se o polígono inscrito na circunferência é um eneágono, sabemos que ele tem 9(nove) lados e também 9(nove) vértices.
A figura resulta em um total de 9(nove) triângulos isósceles congruentes. O ângulo central de cada um será:
$\hat{c} = {{360^{0}}\over 9} = {40}^{0}$
Cada ângulo interno irá valer:
$\hat{i}_{9}= {180^{0}} – {40}^{0}= {140}^{0}$
O apótema divide cada triângulo em dois triângulos retângulos congruentes.
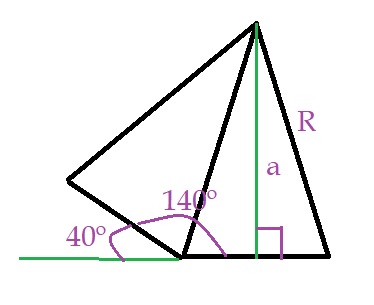
Ele é calculado a partir da da metade do ângulo interno ${70}^{0}$.
$sen(70^{0}) ={a\over R}$
$a = R\cdot sen(70^{0})$
$a = {12,0}\cdot {0,94}$
$a = 11,28\, cm$
Área de um triângulo
Vamos determinar a medida do lado do eneágono.
$R^2 = a^2 + {l\over2}^2$$\Leftrightarrow$${l^2 \over 4} = {12,0}^2 – {11,28}^2 $
$l^2 = 4\cdot{144,0 – 127,24}$$\Leftrightarrow$$\sqrt{l^2}=\sqrt{4\cdot{16,76}}$
$l = 2\cdot {4,09}$$\Leftrightarrow$$l = 8,18\, cm$
$A_{\Delta_{i}} = {{a\cdot l}\over 2}$$\Leftrightarrow$$A_{\Delta_{i}}= {{11,28}\cdot{8,18}\over 2}$
$A_{\Delta_{i}}=46,14\,cm^2$
No polígono há 9(nove) triângulos desses:
$A_{9} = {{46,14}\cdot 9} = 415,26\, cm^2$
02. Determinar o ângulo central, a medida do lado, do apótema, área de cada triângulo e a área do polígono de 15(quinze) lados inscrito em uma circunferência de raio $R=20,0\, cm$.
Ângulo central:
$\hat{c} = {{360}^{0}}{15} = {24}^{0}$
O ângulo interno:
$\hat{i} = {{180}^{0} – {24}^{0} = {156}^{0}$
Isso indica que o ângulo da base do triângulo será:
$\hat{b} = \frac{{156}^{0}}{ 2} = {78}^{0}$
O apótema será: $sen({78}^{0})= \frac{a}{R}$
$a = R\cdot sen({78}^{0})$$\Leftrightarrow$$a = {20,0}\cdot sen({78}^{0})$
$a = {20,0}\cdot {0,9781} = 19,56\,cm$
O lado do polígono irá medir:
$R^2 = a^2 + {\frac{l}{ 2}}^{2}$$\Leftrightarrow$${\frac{l}{2}}^{2} ={20,0}^{2} – {19,56}^{2}$
$l^2 = 4\cdot{400,0 – 382,7081}$$\Leftrightarrow$$\sqrt{l^2} =\sqrt{4\cdot{17,29}}$
$l = 8,32\, cm$
Área de um triângulo
$A_{Delta_15}={{8,32}\cdot{19,56}\over 2}= 81,37\,cm^2$
O polígono terá ao todo:
$A_{15}= {81,37}\cdot{15}=1220,55\,cm^2$
Vamos treinar por conta?!
01. Um dodecágono está inscrito em uma circunferência, cujo raio mede $R= 16,0\,m$. Determine o apótema, o lado do polígono e as áreas de cada triângulo, bem como do polígono todo.
02. O apótema de um polígono regular de 10 lados mede $a = 25,0\, cm$. Determine a medida do raio da circunferência, o lado do polígono, a área de um triângulo e a area total do polígono.
03. Se um polígono de 18 lados tem o lado medindo $l = 20,0\, cm$. Determine o apótema, o raio da circunferência circunscrita, o ângulo interno, a soma dos ângulos internos, a área do polígono.
04. Uma circunferência tem diâmetro $D=60,0 cm$. Inscrevendo-se nela um polígono de 30(trinta) lados, pede-se: a)a medida do ângulo central; b) a medida dos ângulos internos e a soma dos mesmos; c)o número de diagonais do polígono; d)a medida do apótema e do lado do polígono; e)a área de um triângulo e a área total do polígono.
Havendo dúvidas, peça ajuda por meio de um dos canais que seguem listados abaixo.
Curitiba, 14 de fevereiro de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

