Diferença entre conjuntos.
Em artigos anteriores falamos de intersecção, reunião ou união, conjuntos disjuntos. Faltou apenas uma coisa. Diferença entre dois conjuntos A e B.
- Denominamos diferença entre os conjuntos$\color{Navy}{A}$ e $\color{NavyBlue}{B}$, ao conjunto dos elementos pertencentes ao conjunto $\color{NavyBlue}{A}$ , que não pertencem ao conjunto $\color{NavyBlue}{B}$ . Um Diagrama de Venn pode nos mostrar graficamente como é.
- $\color{Brown}{A = \{m, n, o, p, q\}}$
- $\color{Brown}{B =\{p, q, r, s, t\}}$
- $\color{OliveGreen}{A – B = \{m, n, o\}}$ ou $\color{OliveGreen}{A/B = \{m, n, o\}}$
- $\color{OliveGreen}{B – A = \{r, s, t\}}$ ou $\color{OliveGreen}{B/A = \{r, s, t\}}$
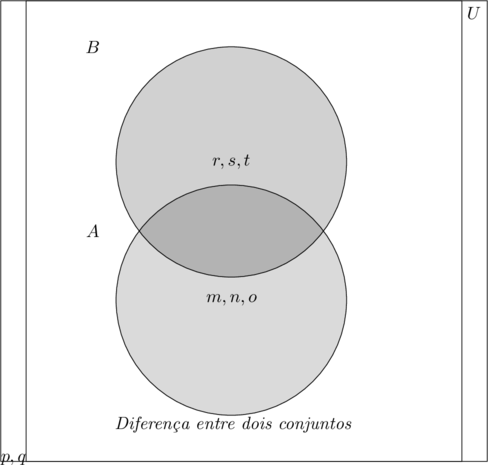
- Os elementos comuns formam a intersecção dos conjuntos A e B.
- $\color{NavyBlue}{ A\cap B = \{ p, q\}}$
- Os conjuntos A e B, contém o conjunto intersecção:
- $\color{OliveGreen}{ A \supset \{ p, q\}}$
- $\color{OliveGreen}{ A \supset \{A \cap B\}} $
- $\color{Brown}{ B \supset \{p, q\}}$
- $\color{Brown}{ B \supset \{B \cap A\}} $
- O conjunto interseção está contido nos conjuntos A e B.
- $\color{OliveGreen}{ \{A\cap B\}\subset A} $
- $\color{OliveGreen}{\{p, q\} \subset A}$
- $\color{Brown}{\{B\cap A\} \subset B}$
- $\color{Brown}{ \{p, q\} \subset B} $
- Veja outro exemplo de diferença entre dois conjuntos $\color{NavyBlue}{C}$ e $\color{NavyBlue}{D}$.
Tomemos os conjuntos
- $\color{NavyBlue}{C = \{1, 2, 3, 4\}}$
- $\color{NavyBlue}{D = \{ 3, 4, 5, 6, 7\}}$
A diferença entre C e D ou D e C é:
- $\color{Brown}{C – D = \{ 1, 2\}}$
- $\color{Brown}{D – C = \{5, 6, 7\}}$
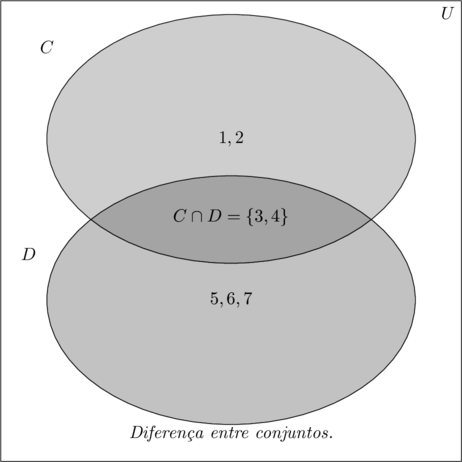
Os elementos que pertencem aos dois conjuntos, não fazem parte do conjunto diferença, e formam o conjunto intersecção.
- $\color{OliveGreen}{C \cap D = \{ 3, 4\}}$
Tanto o conjunto C, quanto o D, contém o conjunto intersecção.
- $\color{Brown}{D\supset \{3, 4\}}$
- $\color{Brown} {D\supset \{ D\cap C \}}$
- $\color{OliveGreen}{C\supset \{3, 4\}}$
- $\color{Olive}{C \supset \{C\cap D\}}$
- Vamos treinar resolvendo os exercícios a seguir. Para facilitar, copie em um caderno ou papel e faça a mão.
- Represente em um Diagrama de Venn, as diferenças entre os conjuntos. Depois escreva na forma entre $\color{Brown}{\{…\}}$ o resultado
- $\color{NavyBlue}{A = \{Merc\acute{u}rio, V\hat{e}nus, Terra, Marte, J\acute{u}piter, Saturno, Urano,\\ Netuno, Plut\tilde{a}o\}}$, $\color{NavyBlue}{ B = \{Terra, Merc\acute{u}rio, V\hat{e}nus, J\acute{u}piter\}}$.
- $\color{NavyBlue}{C = \{ a, b, c, d, e, f, g\}}$ e $\color{NavyBlur}{D = \{a, e, i, o, u\}}$
- $\color{NavyBlue}{ P = \{ m, n, o, p, q\}}$ e $\color{NavyBlue}{Q = \{n, p, q\}}$
- $\color{NavyBlue}{I = \{l, m, n, r, t\}}$ e $\color{NavyBlue}{J =\{n, r, s, t, u\}}$
- Faça a interseção dos conjuntos abaixo. Na forma escrita e no Diagrama de Venn.
- $\color{OliveGreen}{A = \{f, g, h, i, j, l\}}$, $\color{OliveGreen}{B = \{b, c, d, f, g\}}$ $\Rightarrow$ $\color{Brown}{A ∩ B = \{ …\}}$
- $\color{OliveGreen}{D = \{1, 3, 5, 7, 9\}}$, $\color{OliveGreen}{E = \{ 3, 4, 5, 6, 7, 8\}}$ $\Rightarrow$ $\color{Brown}{D\cap E =\{…\}}$
- $\color{OliveGreen}{P = \{ 1, 2, 3, 5, 7, 11, 13\}}$, $\color{OliveGree}{R = \{1, 3, 4, 7, 9\}}$ $\Rightarrow$ $\color{Brown}{P\cap R =\{…\}}$
- $\color{OliveGreen}{H = \{r, s, t, u, v, x, z\}}$, $\color{OliveGreen}{L = \{ k, w, y, v, z\}}$ $\Rightarrow$ $\color{Brown}{H\cap L =\{…\}}$
- Represente em um Diagrama de Venn, as diferenças entre os conjuntos. Depois escreva na forma entre $\color{Brown}{\{…\}}$ o resultado
- Há um caso particular de diferença entre conjuntos. Se um deles é sub-conjunto do outro. Veja o caso do Diagrama de Venn abaixo.
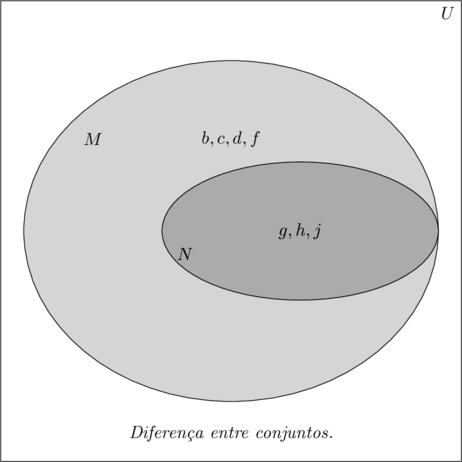
- O conjunto $\color{NavyBlue}{M = \{b,c,d,f,g, h,j\}}$ e o conjunto $\color{NavyBlue}{N = \{ g, h, j\}}$. Podemos notar que todos os elementos do conjunto$\color{NavyBlue}{N}$, também pertencem ao conjunto $\color{NavyBlue}{M}$. A interseção desses conjuntos será igual ao conjunto $\color{NavyBlue}{N}$.
- $\color{OliveGreen}{M\cap N = N }$
- A diferença entre eles fica:
- $\color{OliveGreen}{M – N = \{b, c, d, f\}}$
- $\color{OliveGreen}{ N – M = \varnothing }$
- Obs.: Neste caso o conjunto diferença é vazio, pois todos os elementos de N pertencem também a M.
- Dizemos que a diferença entre M e N é o complemento ou complementar de N em M. Em outras palavras, a diferença é o conjunto dos elementos que faltam em $\color{NavyBlue}{N}$ para que ele se torne igual a $\color{NavyBlue}{M}$. Isso permite dizer que a união do conjunto $\color{NavyBlue}{N}$ com o conjunto diferença é o conjunto $\color{NavyBlue}{M}$. Simbolicamente fica.
- $\color{OliveGreen}{M – N = \{ b, c, d, f\}}$
- $\color{OliveGreen}{ N \cup (M – N) = M}$
- $\color{OliveGreen}{N – M = \varnothing}$
- $\color{OliveGreen}{M\cup \varnothing = M}$
- Se definirmos um Conjunto Universo U, todos os conjuntos que podemos formar com os elementos desse universo, são sub-conjuntos deste. O conjunto complementar de um sub-conjunto A em relação ao Universo, pode ser representado por: $\color{NavyBlue}{C(A)}$.
- $\color{NavyBlue}{U = \{ alfabeto\}}$
- Tomemos como universo o conjunto das letras do alfabeto.
- Seja um sub-conjunto desse universo, o conjunto das vogais.
- $\color{OliveGreen}{A = \{a, e, i, o, u\}}$
- O complementar de $\color{OliveGreen}{A}$, nesse caso, em relação ao universo, será o conjunto das consoantes, isto é, o alfabeto, retiradas as vogais.
- $\color{Brown}{C(A) = \{consoantes\}}$
- Ou então $\color{OliveGreen}{U = \{x \in (Impares) | 0\lt x \lt 50 \}}$
- Seja $\color{NavyBlue}{A = \{x’ \in (Impares)| 0\lt x’\lt 10\}}$
- Nesse caso o $\color{OliveGreen}{C(A) = \{y \in (Impares) |{10}\lt y \lt{50}\}}$
- Ou então $\color{OliveBlue}{B = \{ x” \in (Impares) |{35}\lt x” \lt {50}\}}$
- Teremos $\color{OliveGreen}{C(B) = \{z \in (Impares) |0\lt z\lt {35}\}} $
- Mais um exercício para concluir.
- Dados os conjuntos: $\color{NavyBlue}{A = \{a, b, c, d, e, f, g\}}$, $\color{NavyBlue}{B = \{ b, c, d, f\}}$ e $\color{NavyBlue}{C = \{a, e\}}$, efetue as operações a seguir.
- $\color{OliveGreen}{ A – B = \{ …\}}$
- $\color{OliveGreen}{ A-C = \{…\}}$
- $\color{OliveGreen}{ C – A = ?}$
- $\color{OliveGreen}{ C – B = ?}$
- $\color{OliveGreen}{B – C = ?}$
- $\color{OliveGreen}{B – A = ?}$
OBS.: Não esqueça! Em caso de dificuldade, entre em contato por um dos meios abaixo citados. Estou pronto para ajudar.
Revisado e melhorado em 08 de julho de 2016. Republicado em 06 de novembro de 2017.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celulares e WhatsApp: (41) 99805-0732

