Tag: #igualdades trigonométricas

Publicado em

Resolução de exercícios de trigonometria.

Exercícios propostos para treino no post anterior

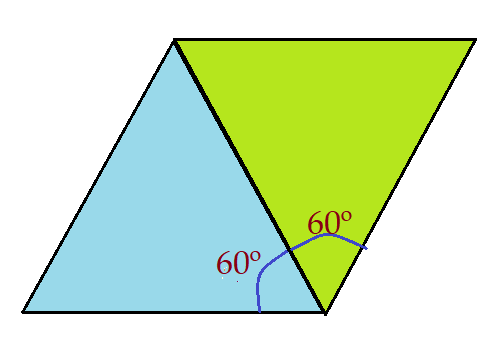
Triângulos isósceles equiláteros justapostos, formando losango.

01. Se um triângulo isósceles tem o ângulo oposto à base, medindo $\alpha = 60^{0}$, determine o seno e o cosseno do ângulo resultante da justaposição de dois desses triângulos, como mostra a figura.

Sendo um triângulo isósceles e um de seus ângulos mede $\alpha = 60^{0}$, é fácil deduzir que se trata de um triângulo equilátero e os outros dois ângulos têm a mesma medida. Assim, na justaposição como mostra a figura, o que está sendo pedido é $sen{(\alpha + \alpha)}$ e $cos{(\alpha + \alpha)}$. Em outras palavras temos um ângulo duplo.

Indo até a tabela das igualdades ou relações trigonométricas, encontraremos:

$\color{navy}{sen{(2\alpha)} = 2sen\alpha\cdot cos\alpha}$

$\color{navy}{cos{(2\alpha)} = cos^2\alpha – sen^2\alpha}$

Sabemos que $sen{60^{0}} = {\sqrt{3}\over 2}$ e que $cos{60}={1\over2}$, podemos substituir e obter o resultado.

$sen{(2\cdot {60^{0}})} = 2\cdot sen{60^{0}}\cdot cos{60^{0}}$

$sen{(120{0})} = 2\cdot {\sqrt{3}\over 2}\cdot{1\over 2}$

$sen{(120{0})} = 2\cdot{\sqrt{3}\over4} = {\sqrt{3}\over2} $

$\color{maroon}{sen{(120^{0})} = {\sqrt{3}\over 2}}$

$cos{(2\cdot{60º})} = cos^2{60^{0}} – sen^2{60^{0}}$=${{\left(1\over2\right)^2} – {\left(\sqrt{3}\over2\right)^2}}$

$cos{(120^{0})} = {1\over4} – {3\over 4} = -{\not{2}\over\not{4}}$

$\color{maroon}{cos{(120^{0})} = -{1\over 2}}$

02. Sabendo que um ângulo $\beta$ mede mede $30^{0}$ e o outro $\alpha$ mede $45^{0}$. Determine a tangente e cotangente da soma desses dois ângulos.

Consultando a tabela das igualdades, encontraremos que:

$\color{navy}{tg{(\alpha\pm \beta)}={{1+ tg\beta\cdot ctg\alpha}\over{ctg\alpha \mp tg\beta}}}$

$\color{navy}{ctg{(\alpha \pm \beta)}={{ctg\alpha\mp tg\beta}\over{1\pm tg\beta\cdot ctg\alpha}}}$

Precisamos então saber os valores da tangente e cotangente dos dois ângulos. Podemos ver na tabela, vista anteriormente e encontraremos:

$tg\alpha = 1$; $ctg\alpha = 1$

$tg\beta = {\sqrt{3}\over 2}$; $ctg\beta = \sqrt{3}$

Então:

$tg{(30^{0} + 45^{0})}={{1+{1}\cdot\sqrt{3}}\over{\sqrt{3} – 1}}$

$tg{(75^{0})} = {{1 +\sqrt{3}}\over {\sqrt{3}-1}}$=${{(1 +\sqrt{3})}\cdot{(\sqrt{3} + 1)}}\over{{(\sqrt{3} -1)}\cdot{\sqrt{3} + 1}}$

$tg{(75^{0})} = {{1 +2\sqrt{3} +\sqrt{3}^2}\over{\sqrt{3}^2 – 1^2}}$=${{\not{4} +\not{2}\sqrt{3}}\over\not{4}}$

$\color{maroon}{tg(75{0}) = 2 + \sqrt{3}}$

Agora a cotangente

$ctg{(45º + 30º)}={{ctg(30º) – tg(45º)}\over{1 + tg(45º)\cdot ctg(30º)}}$=${{\sqrt{3} – 1}\over{1+1\cdot\sqrt{3}}}$

$ctg(75^{0}) = {{{(\sqrt{3} -1)}\cdot{(1 -\sqrt{3})}}\over{{(1+\sqrt{3})}\cdot{(1-\sqrt{3})}}}$=${{2\sqrt{3} -3 -1}\over{1 – 3}}$ = ${{\not{2}\sqrt{3} -\not{4}}\over{-2}}$

$\color{maroon}{ctg(75^{0})= 2 -\sqrt{3}}$

03. Se a secante de um ângulo é $\color{green}{sec\alpha = 3}$, determine: a) $cos\alpha$; b) $sen\alpha$; c)$cos{2\alpha}$; d)$sen{2\alpha}$.

É fornecido que $\color{green}{sec\alpha = 3}$ e pede-se:

a)$cos\alpha$

Por definição $sec\alpha = {1\over cos\alpha}$

Daí tiramos que: $cos\alpha = {1\over sec\alpha}$

Substituímos: $cos\alpha = {1\over 3}$

$\color{maroon}{cos\alpha = {1\over3}}$

b) $sen\alpha$ ?

A relação fundamental da trigonometria nos diz que:

$sen^2\alpha + cos^2\alpha = 1$

$sen^2\alpha + {\left(1\over 3\right)^2} = 1$=$sen^2\alpha = 1 -{1\over 9}$=${{9 – 1}\over9}$

$\sqrt{sen^2\alpha} = \sqrt{8\over9}$ = ${\sqrt{2\cdot 2}\over\sqrt{9}}$

$\color{maroon}{sen\alpha = {2\sqrt{2}\over 3}}$

c)Na tabela de igualdades encontramos que:

$\color{navy}{cos{2\alpha} = cos^2\alpha – sen^2\alpha}$

Substituindo os valores acima, temos:

$cos{(2\alpha)}= {\left(1\over3\right)^2} – {\left(2\sqrt{2}\over 3\right)}^2$=${{1\over 9} – {{2^2\cdot 2}\over 9}}$

$cos{(2\alpha)} = {{1 – 8}\over 9}$=$-{7\over9}$

$\color{maroon}{cos{(2\alpha)} = -{7\over 9}}$

d)Voltando à tabela de igualdades:

$\color{navy}{sen{(2\alpha)} = 2sen\alpha\cdot cos\alpha}$

Substituindo: $sen{(2\alpha)}={2\cdot {2\sqrt{2}\over3}\cdot{1\over3}}$

$\color{maroon}{sen{(2\alpha)} = {4\sqrt{2}\over9}}$

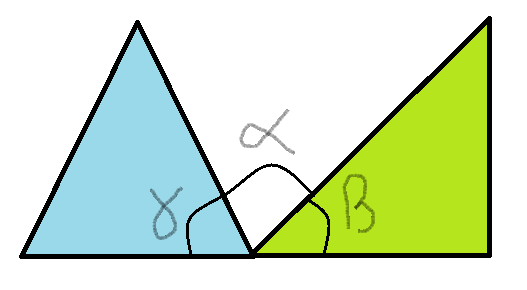
Triângulos contíguos, com um vértice comum.

04. Dois triângulos são colocados lado a lado, de modo a fazer coincidir um de seus vértices da base. O primeiro é equilátero e o segundo isósceles, onde o ângulo do vértice superior mede $45^{0}$. Determine: a) o seno do ângulo entre os lados dos dois triângulos $\color{red}{\alpha}$; b) o cosseno da soma do ângulo interno do equilátero e o lado do isósceles$\color{red}{(\alpha + \gamma)}$; c) o seno do ângulo formado entre a base do isósceles e o lado do equilátero$\color{red}{(\alpha + \beta)}$.

Os dois triângulos formam o ângulo $\alpha$. Sendo um deles equilátero, seus ângulos são iguais e medem $(60^{0})$. O outro é isósceles e se um de seus ângulos agudos mede $(45^{0})$, não resta dúvida sobre a medida do outro ângulo, que é igual a este. A figura mostra os triângulos colocados de modo que os vértices coincidem. Os ângulos somados totalizam $(180^{0})$, isto é, um ângulo raso.

Temos pois: $\gamma = 60^{0}$ e $\beta = 45^{0}$.

a) $\gamma + \alpha + \beta = 180^{0}$

$(60^{0}) + \alpha + (45^{0}) = (180^{0})$$\Leftrightarrow$$\alpha = (180^{0}) – (105^{0}) = (75^{0})$

b)$\color{navy}{cos{(\gamma + \alpha)} = {cos\gamma\cdot cos\alpha – sen\alpha\cdot sen\gamma}}$

$cos{(60^{0}+ 75^{0})}={cos(60^{0})\cdot cos(75^{0}) – sen(75^{0})\cdot sen(60{0})}$ (I)

É necessário determinar os valores do seno e do cosseno de $75^{0}$. Sabemos que $45^{0}+ 30^{0} = 75^{0}$. Logo:

$sen{(45^{0} + 30^{0})}={sen^(45{0})\cdot cos(30^{0}) + sen(30^{0})\cdot cos(45^{0})}$

$sen(75^{0}) = {{\sqrt{2}\over2}\cdot{\sqrt{3}\over2} + {1\over2}\cdot{\sqrt{2}\over 2}}$=${\sqrt{6}\over 4} + {\sqrt{2}\over 4}$

$\color{maroon}{sen(75^{0})={{\sqrt{6} + \sqrt{2}}\over 4}}$ (II)

$cos(45^{0}+30^{0})={cos(45^{0})\cdot cos(30^{0}) – sen(45^{0})\cdot sen(30^{0})}$

$cos(75^{0})={{\sqrt{2}\over2}\cdot{\sqrt{3}\over 2} – {\sqrt{2}\over 2}\cdot{1\over2}}$=${{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}$

$\color{maroon}{cos(75^{0})={{\sqrt{6} -\sqrt{2}}\over4}}$ (III)

Substituindo (II) e (III) em (I), teremos:

$cos(60^{0} + 75^{0})={{1\over 2}\cdot {{\sqrt{6}-\sqrt{2}}\over4} – {{\sqrt{3}\over 2}\cdot{\sqrt{6} +\sqrt{2}\over 4}}}$

$cos(60^{0}+75^{0})={{\sqrt{6} -\sqrt{2}}\over 8} -{{\sqrt{18} +\sqrt{6}}\over 8}$=${{\sqrt{6} -\sqrt{2} -3\sqrt{2} -\sqrt{6}}\over 8}$

$cos(135^{0}) = {{\sqrt{6}-\sqrt{6} – \not{4}\sqrt{2}}\over\not{8}}$=$ -{\sqrt{2}\over 2}$

$\color{maroon}{cos(135^{0}) =-{\sqrt{2}\over2}}$

c)$sen(45^{0} + 75^{0})={sen(45^{0})\cdot cos(75^{0}) + sen(75^{0})\cdot cos(45^{0})}$

$sen{120^{0}) = {\sqrt{2}\over2}\cdot{{\sqrt{6} -\sqrt{2}}\over 4} +{{\sqrt{6} + \sqrt{2}}\over 4}\cdot{\sqrt{2}\over2}}$=${{\sqrt{12}-\sqrt{4}}\over 8} + {{\sqrt{12} + \sqrt{4}}\over 8}$

$sen(120^{0}) = {{2\sqrt{3}- 2}\over 8} + {{2\sqrt{3} + 2}\over 8}$=${4\sqrt{3}\over 8}$=${\sqrt{3}\over2}$

$\color{maroon}{sen(120^{0})= {\sqrt{3}\over 2}}$

05. Sendo os ângulos $\color{Red}{\alpha = 60^{0}}$ e $\color{Red}{\beta = 45^{0}}$, determine: a) $cos{(\alpha – \beta)}$; b)$sen{(\alpha – \beta)}$; c)$tg{(\alpha – \beta)}$.

Dados: $\alpha=60^{0}$ e $\beta=45^{0}$

$sen(60^{0})={\sqrt{3}\over2}$; $cos(60^{0})={1\over2}$

$sen(45^{0})={\sqrt{2}\over2}$; $cos(45^{0})={\sqrt{2}\over2}$

a)$\color{navy}{cos{(\alpha-\beta)}={cos\alpha\cdot cos\beta + sen\alpha\cdot sen\beta}}$

$cos(60^{0}-45^{0}) ={cos(60^{0})\cdot cos(45^{0}) + sen(60^{0})\cdot sen(45^{0})}$=${{1\over2}\cdot{\sqrt{2}\over2} +{\sqrt{3}\over2}\cdot{\sqrt{2}\over2}}$

$cos(15^{0}) = {\sqrt{2}\over4} + {\sqrt{6}\over4}$=${{\sqrt{2}+\sqrt{6}}\over4}$

$\color{maroon}{cos(15^{0})={{\sqrt{6}+\sqrt{2}}\over4}}$

b)$\color{navy}{sen{(\alpha -\beta)}={sen(\alpha)\cdot cos(\beta)-sen(\beta)\cdot cos(\alpha)}}$

$sen(60^{0}-45^{0})={sen(60^{0})\cdot cos(45^{0})-sen(45^{0})\cdot cos(60^{0})}$

$sen(15^{0})={{\sqrt{3}\over2}\cdot{\sqrt{2}\over2}-{\sqrt{2}\over2}\cdot{1\over2}}$=${{\sqrt{6}\over4}-{\sqrt{2}\over4}}$

$\color{maroon}{sen(15^{0})={{\sqrt{6}-\sqrt{2}}\over4}}$

c)$\color{navy}{tg{(\alpha-\beta)}={{1-tg\beta\cdot ctg\alpha}\over{ctg\alpha + tg\beta}}}$

$tg(60^{0}-45^{0})={{1-tg(45^{0})\cdot ctg(60^{0})}\over{ctg(60^{0})+tg(45^{0})}}$

$tg(15)={{1-{1\cdot\sqrt{3}\over3}}\over{{\sqrt{3}\over 3}+ 1}}$

$tg(15^{0})={{{3 – \sqrt{3}}\over\not{3}}\over{{3 + \sqrt{3}}\over\not{3}}}$=${{(3 – \sqrt{3})}\cdot{(3-\sqrt{3})}\over{{(3+\sqrt{3})}\cdot{(3-\sqrt{3})}}}$

$tg(15^{0})={{3^2 -2\cdot\sqrt{3} + {\sqrt{3}}^2}\over{3^2-{\sqrt{3}}^2}}$=${{9 + 3 – 2\sqrt{3}}\over{9 – 3}}$

$tg(15^{0})={{12 – 2\sqrt{3}}\over6}$=${{6-\sqrt{3}}\over 3}$

$\color{Maroon}{tg(15^{0})={{6 – \sqrt{3}}\over3}}$

06. Calcular as demais razões trigonométricas sabendo que $\color{Red}{tg\alpha = {4\over 3}}$ α pertence ao primeiro quadrante($0^{0}<\alpha<90^{0}$.

Vimos em postagens anteriores que $tg\alpha ={
sen\alpha\over cos\alpha}$. Então podemos escrever:

$tg\alpha = {sen\alpha\over cos\alpha} = {4\over3}$

$sen\alpha = {4\over3}\cdot cos\alpha$ (I)

Da relação fundamental temos:

$sen^2\alpha + cos^2\alpha = 1$ (II)

Substituimos (I) em (II):

$\left({{4\over3}\cdot cos\alpha}\right)^2+cos^2\alpha =1$

${{16}\over9}\cdot cos^2\alpha + cos^2\alpha = 1$$\Leftrightarrow$${{16 + 9}\over9}\cdot cos^2\alpha =1$

${{25}\over9}\cdot cos^2\alpha =1$$\Leftrightarrow$$cos^2\alpha= {9\over{25}}$

$\sqrt{cos^2\alpha} = \sqrt{9\over{25}}$$\Leftrightarrow$$cos\alpha = {3\over5}$

$\color{Maroon}{cos\alpha = {3\over5}}$

Substituindo em $sen\alpha = {4\over3}\cdot cos\alpha$

$sen\alpha = {4\over\not{3}}{\not{3}\over5} = {4\over5}$

$\color{maroon}{sen\alpha = {4\over5}}$

$\color{navy}{ctg\alpha = {1\over tg\alpha}}$$\Leftrightarrow$$ctg\alpha={1\over{4\over3}} = {3\over4}$

$\color{maroon}{ctg\alpha = {3\over4}}$

$\color{NavyBlue}{sec\alpha = {1\over cos\alpha}}$

$sec\alpha = {1\over{3\over5}}= {5\over3}$

$\color{Maroon}{sec\alpha = {5\over 3}}$

$\color{NavyBlue}{csc\alpha = {1\over sen\alpha}}$

$csc\alpha={1\over{4\over5}} = {5\over4}$

$\color{Maroon}{csc \alpha={5\over4}}$

07. Demostrar as seguintes igualdades trigonométricas.

Na demonstração das igualdades devemos encontrar uma forma de mostrar que a igualdade é verdadeira. Vamos ver como é que se faz isso.

a)$\color{NavyBlue}{\left[{{(1 – sen\alpha)}\over {cos\alpha}}\right] = \left[{{cos\alpha}\over{(1 + sen\alpha)}}\right]}$;

Aqui temos uma proporção, onde o produto dos meios é igual ao produto dos extremos. Vamos ver no que isso resulta.

${(1-sen\alpha)}\cdot{(1+sen\alpha)} = {cos\alpha\cdot cos\alpha}$

${1 – sen\alpha + sen\alpha – sen^2\alpha} = cos^2\alpha$

${1 – sen^2\alpha} = cos^2\alpha$

$ 1 = sen^2\alpha + cos^2\alpha$

Recaímos na relação fundamental da trigonometria e podemos dizer que $ 1 = 1$. Fica demonstrada a validade da igualdade.

b) $\left[{{(sen\alpha + ctg\alpha)}\over{(tg\alpha + cosec\alpha)}}\right] = cos\alpha$;

$\left[{{\left({sen\alpha\over 1} + {cos\alpha\over sen\alpha}\right)}\over{\left({sen\alpha\over cos\alpha}+{1\over sen\alpha}\right)}}\right] = cos\alpha$

$\left[{\left({{sen^2\alpha +cos\alpha}\over sen\alpha}\right)}\over{\left({sen^2\alpha + cos\alpha}\over{sen\alpha\cdot cos\alpha}\right)}\right] = cos\alpha$

Efetuando a divisão

$\left({{sen^2\alpha + cos\alpha}\over sen\alpha}\right)\cdot\left({{sen\alpha\cdot cos\alpha}\over{sen^2\alpha + cos\alpha}}\right) = cos\alpha$

Simplificando fica:

$\color{Maroon}{cos\alpha = cos\alpha}$

c)$\color{NavyBlue}{{tg\alpha + ctg\alpha} = sec\alpha\cdot csec\alpha}$;

Substituindo por expressões equivalentes, fica:

$\left({{sen\alpha\over cos\alpha} + {cos\alpha\over sen\alpha}}\right) = \left({{1\over cos\alpha}\cdot{1\over sen\alpha}}\right)$

Reduzindo o primeiro membro ao mesmo denominador:

$\left({{sen^2\alpha + cos^2\alpha}\over{sen\alpha\cdot cos\alpha}}\right) = \left({1\over{sen\alpha\cdot cos\alpha}}\right)$

Multiplicando os meios da proporção:

${sen^2\alpha + cos^2\alpha} = \left({{sen\alpha\cdot cos\alpha}\over{sen\alpha\cdot cos\alpha}}\right)$

$\color{Maroon}{sen^2\alpha + cos\alpha = 1}$

d)$\color{navy}{cos^2\alpha = sen^2\alpha\cdot cos^2\alpha + cos^4\alpha}$

Fatorando o segundo membro, temos:

$cos^2\alpha = cos^2\alpha\cdot{sen^2\alpha + cos^2\alpha}$

Cancelando os fatores comuns entre os dois membros:

$\color{Maroon}{1 = sen^2\alpha + cos^2\alpha}$

08. Faça a demonstração das igualdades trigonométricas:

a)$\color{NavyBlue}{{2tg x\left({{1 + cos x}\over2}\right)} = {sen x + tg x}}$

Simplificando os fatores comuns entre numerador e denominador, depois substituindo $tg x = {sen x\over cos x}$

${\not{2}\cdot tg x\left({{1 + cos x}\over\not{2}}\right)}=sen x + tg x$

${\left({sen x\over cos x}\right)\cdot{(1 + cos x)}} = sen x + {(sen x\over cos x)}$

${\left({sen x\over cos x} + {{sen x\cdot cos x}\over cosx}\right)} = {\left({sen x\cdot cos x + sen x}\over cos x\right)}$

$\color{Maroon}{tg x + sen x = sen x + tg x}$

b)$\color{NavyBlue}{\left[{\left({tg\alpha + tg\beta}\right)\over\underbrace{\left({ctg\alpha + ctg\beta}\right)}}\right]=\overbrace{{tg\alpha\cdot tg\beta}}}$

Trocando de posição as expressões assinaladas fica:

$\left[{\left({tg\alpha + tg\beta}\right)\over{\left(tg\alpha\cdot tg\beta\right)}}\right] = \left({ctg\alpha + ctg\beta}\right)$

Separando em duas frações com mesmo denominador:

$\left[{\left({tg\alpha\over{tg\alpha\cdot tg\beta}}\right) +\left({tg\beta\over{tg\alpha\cdot tg\beta}}\right)}\right] =\left({ctg\alpha + ctg\beta}\right)$

$\color{maroon}{ctg\beta + ctg\alpha = ctg\alpha + ctg\beta}$

09. Demonstrar as seguintes igualdades trigonométricas

a)$\color{navy}{sec^2\alpha + csc^2\alpha = sec^2\alpha\cdot csc^2\alpha}$

$\left({{1\over cos^2\alpha} + 1\over sen²\alpha}\right) = \left({{1\over cos^2\alpha}\cdot{1\over sen^2\alpha}}\right)$

Reduzindo ao mesmo denominador:

$\left({{sen^2\alpha + cos^2\alpha}\over{cos^2\alpha\cdot sen^2\alpha}}\right) =\left({1\over{cos^2\alpha\cdot sen^2\alpha}}\right)$

Cancelando os denominadores iguais;

$\color{Maroon}{sen^2\alpha + cos^2\alpha = 1}$

b)$\color{NavyBlue}{\left[{{sen\alpha\cdot cos\alpha}\over{sen^2\alpha – cos^2\alpha}}\right] = \left[{{tg\alpha}\over{tg^2\alpha -1}}\right]}$

$ \left[{{sen\alpha\cdot cos\alpha}\over{sen^2\alpha – cos^2\alpha}}\right] = \left[{{\left(sen\alpha\over cos\alpha\right)}\over\left({{sen^2\alpha\over cos^2\alpha}-1}\right)}\right]$

$\left[{{sen\alpha\cdot cos\alpha}\over{sen^2\alpha – cos^2\alpha}}\right]=\left[{{\left(sen\alpha\over cos\alpha\right)}\over\left({{sen^2\alpha – cos^2\alpha}\over cos^2\alpha}\right)}\right]$

$\left[{{sen\alpha\cdot cos\alpha}\over{sen^2\alpha – cos2\alpha}}\right]= \left[{{sen\alpha\cdot cos^2\alpha}\over{cos\alpha\cdot\left({sen^2\alpha – cos^2\alpha}\right)}}\right]$

Simplificando os fatores comuns e cancelando os denominadores iguais, ficamos com:

$\color{Maroon}{sen\alpha\cdot cos\alpha = sen\alpha\cdot cos\alpha}$

c)$\color{navy}{{\left(sec\alpha – tg\alpha\right)^2}=\left({{1 – sen\alpha}\over{1 + sen\alpha}}\right)}$

$\left({{1\over cos\alpha} – {sen\alpha\over cos\alpha}}\right)^2 =\left({{1 – sen\alpha}\over{1 + sen\alpha}}\right)$

$\left[{\left({1 – sen\alpha}\right)^2\over cos^2\alpha}\right]= \left({{1 – sen\alpha}\over{1 + sen\alpha}}\right)$

Cancelando o fator comum entre os dois membros:

$\left({{1 – sen\alpha}\over{cos^2\alpha}}\right)= \left({1\over{1 + sen\alpha}}\right)$

Multiplicando os meios e os extremos entre si:

${(1 – sen\alpha)}{(1 + sen\alpha)} = cos^2\alpha$

${1 – sen^2\alpha = cos^2\alpha}$$\Leftrightarrow$$1 = sen^2\alpha + cos^2\alpha$

$\color{Maroon}{sen^2\alpha + cos^2\alpha = 1}$

10. Demonstre as seguintes identidades trigonométricas.

a)$\color{navy}{sen\alpha + cos\alpha = \left({{1 + tg\alpha}\over sec\alpha}\right)}$

$sen\alpha + cos\alpha = \left({{{1 + {sen\alpha\over cos\alpha}}\over{1\over cos\alpha}}}\right)$=$\left({{{cos\alpha + sen\alpha}\over cos\alpha}}\cdot{cos\alpha\over 1}\right)$

Simplificando os fatores comuns entre numerador e denominador.

$\color{Maroon}{sen\alpha\cdot cos\alpha = cos\alpha\cdot sen\alpha}$

b)$\color{NavyBlue}{\left({{cos\alpha + tg\alpha}\over{cos\alpha\cdot tg\alpha}}\right)= \left({ctg\alpha + sec\alpha}\right)}$

$\left[{{cos\alpha +\left({sen\alpha\over cos\alpha}\right)}\over{cos\alpha\cdot\left({sen\alpha\over cos\alpha}\right)}}\right]=\left({ctg\alpha + sec\alpha}\right)$

$\left[{{{cos^2\alpha + sen\alpha\cdot cos\alpha}\over cos\alpha}\over{{cos\alpha\cdot sen\alpha}\over cos\alpha}}\right] = \left({ctg\alpha + sec\alpha}\right)$

$\left[{\left({{cos^2\alpha + sen\alpha\cdot cos\alpha}\over cos\alpha}\right)\cdot\left({cos\alpha\over{cos\alpha\cdot sen\alpha}}\right)}\right] = \left({ctg\alpha + sec\alpha}\right)$

Cancelando fatores comuns entre numerador e denominador.

$\left[{{cos^2\alpha\over{cos\alpha\cdot sen\alpha}} + {sen\alpha\over{cos\alpha\cdot sen\alpha}}}\right] = \left({ctg\alpha + sec\alpha}\right)$

$\left[{{cos\alpha\over sen\alpha} + {1\over cos\alpha}}\right]=\left({ctg\alpha + sec\alpha}\right)$

$\color{Maroon}{ctg\alpha + sec\alpha = ctg\alpha + sec\alpha}$

c)$\color{NavyBlue}{\left({2sen\alpha\over {tg(2\alpha)}}\right)= cos\alpha – \left({sen^2\alpha\over cos\alpha}\right)}$

Sabemos que $tg(2\alpha) = {2\over{ctg\alpha – tg\alpha}}$

$\left[{2sen\alpha\over{2\over{ctg\alpha – tg\alpha}}}\right]=cos\alpha – \left({sen^2\alpha\over cos\alpha}\right)$

$\left[{\not{2}sen\alpha\cdot\left({ctg\alpha – tg\alpha}\right)\over \not{2}}\right]=cos\alpha – \left({sen²\alpha\over cos\alpha}\right) $

$\left[{sen\alpha\cdot\left({{cos\alpha\over sen\alpha} – {sen\alpha\over cos\alpha}}\right)}\right]=cos\alpha – \left({sen^2\alpha\over cos\alpha}\right) $

$\color{Maroon}{cos\alpha – {sen^2\alpha\over cos\alpha}=cos\alpha – {sen^2\alpha\over cos\alpha}}$

11. Demonstrar as seguintes igualdades trigonométricas.

a)$\color{NavyBlue}{{1 + sen\alpha\cdot tg\alpha}= \left({{sen\alpha + ctg\alpha}\over{ctg\alpha}}\right)}$

${1 + sen\alpha\cdot\left({sen\alpha\over cos\alpha}\right)} = \left[{{sen\alpha +\left({cos\alpha\over sen\alpha}\right)}\over\left({cos\alpha\over sen\alpha}\right)}\right]$

$\left({{cos\alpha + sen^2\alpha}\over cos\alpha}\right)=\left[{\left({{sen^2\alpha + cos\alpha}\over sen\alpha}\right)\over\left({cos\alpha\over sen\alpha}\right)}\right]$

$\left({{cos\alpha + sen^2\alpha}\over cos\alpha}\right)=\left[{\left({{sen^2\alpha + cos\alpha}\over sen\alpha}\right)\cdot\left({sen\alpha\over cos\alpha}\right)}\right]$

Simplificando os fatores comuns, ficamos com:

$\color{Maroon}{cos\alpha + sen^2\alpha = sen^2\alpha + cos\alpha}$

b)$\color{NavyBlue}{tg\alpha + ctg\alpha = \left({1\over{sen\alpha\cdot cos\alpha}}\right)}$

$\left({{sen\alpha\over cos\alpha} + {cos\alpha\over sen\alpha}}\right) = \left({1\over{sen\alpha\cdot cos\alpha}}\right)$

$\left({{sen^2\alpha + cos^2\alpha}\over{sen\alpha\cdot cos\alpha}}\right)=\left({1\over{sen\alpha\cdot cos\alpha}}\right)$

Cancelando os denominadores iguais, obtemos a relação fundamental da trigonometria.

$\color{Maroon}{sen^2\alpha + cos^2\alpha = 1}$

c)$\color{NavyBlue}{\left({sen\alpha + cos\alpha}\right)^2 +\left({sen\alpha – cos\alpha}\right)^2 =2}$

$\left({sen^2\alpha + 2\cdot sen\alpha\cdot cos\alpha + cos^2\alpha}\right) + \left({sen^2\alpha – 2\cdot sen\alpha\cdot cos\alpha + cos^2\alpha}\right) = 2$

Reduzindo os termos semelhantes:

$2\cdot sen^2\alpha + 2\cdot cos^2\alpha = 2$$\Leftrightarrow$$2{sen^2\alpha + cos^2\alpha} = 2$

Dividindo ambos os membros por $2$;

$\color{Maroon}{sen^2\alpha + cos^2\alpha = 1}$

12. Calcular as restantes razões trigonométricas sabendo que $ sen\alpha={3\over5} $ e $0^{0}<\alpha<90^{0}$, isto é pertence ao primeiro quadrante.

Começaremos por determinar o cosseno desse ângulo, mediante o uso da relação fundamental.

$\color{NavyBlue}{sen^2\alpha + cos^2\alpha = 1}$

$\left({3\over 5}\right)^2 + cos^2\alpha = 1$$\Leftrightarrow$$cos^2\alpha = {1 – {9\over {25}}}$

$cos^2\alpha ={{{25} – 9}\over{25}}$$\Leftrightarrow$$\sqrt{cos^2\alpha}=\sqrt{{16}\over{25}}$

$\color{Maroon}{cos\alpha = {4\over5}}$

Agora temos os valores de seno e cosseno, o que nos permite calcular as demais razões do ângulo.

$\color{NavyBlue}{tg\alpha = {sen\alpha\over cos\alpha}}$

$tg\alpha = \left[{\left({3\over5}\right)\over\left({4\over5}\right)}\right]$

$tg\alpha = \left({3\over\not{5}}\right)\cdot\left({\not{5}\over4}\right)$

$\color{Maroon}{tg\alpha = {3\over4}}$

$\color{NavyBlue}{sec\alpha = {1\over cos\alpha}}$

$sec\alpha = {1\over{4\over5}}$=${5\over4}$

$\color{Maroon}{sec\alpha = {5\over4}}$

$\color{NavyBlue}{csc\alpha = {1\over sen\alpha}}$

$csc\alpha = {1\over{3\over5}}$=${5\over3}$

$\color{Maroon}{csc\alpha ={5\over3}}$

13. Calcular as restantes razões trigonométricas sabendo que o $cos\alpha=5\over 13}$ e $ \alpha$ pertence ao primeiro quadrante.

Aqui seguiremos os mesmos passos do exercício anterior.

$\color{NavyBlue}{sen^2\alpha + cos^2\alpha = 1}$

$sen^2\alpha +\left({5\over{13}}\right)^2 = 1$$\Leftrightarrow$$sen^2\alpha + {{25}\over {169}} = 1$

$sen^2\alpha = 1 -{{25}\over{169}}$$\Leftrightarrow$$sen^2\alpha = {{{169} – {25}}\over{169}}$

$\sqrt{sen^2\alpha} = \sqrt{{144}\over{169}}$=${{12}\over{13}}$

$\color{Maroon}{sen\alpha = {{12}\over{13}}}$

$\color{NavyBlue}{tg\alpha = \left({sen\alpha\over cos\alpha}\right)}$

$tg\alpha = \left[{\left({{12}\over{13}}\right)\over\left({5\over{13}}\right)}\right]$

$tg\alpha = \left({{12}\over{13}}\right)\cdot\left({{13}\over5}\right)$=${{12}\over5}$

$\color{Maroon}{tg\alpha = {{12}\over5}}$

$\color{NavyBlue}{ctg\alpha = {cos\alpha\over sen\alpha}}$

$ctg\alpha = \left[{\left({5\over{13}}\right)\over\left({{12}\over{13}}\right)}\right]$$\Leftrightarrow$$ctg\alpha = \left({5\over{13}}\right)\cdot\left({{13}\over{12}}\right)$

$\color{Maroon}{ctg\alpha = {5\over{12}}}$

$\color{NavyBlue}{sec\alpha ={1\cos\alpha}}$

$sec\alpha = \left[{1\over\left({5\over{13}}\right)}\right]$=${{13}\over5}$

$\color{Maroon}{sec\alpha = {{13}\over5}}$

$\color{NavyBlue}{csc\alpha = {1\over sen\alpha}}$

$csc\alpha = \left[{1\over\left({{12}\over{13}}\right)}\right]$=${{13}\over{12}}$

$\color{Maroon}{csc\alpha = {{13}\over{12}}}$

14. Calcular as restantes razões trigonométricas sabendo que $ tg\alpha={4\over 3}$ e $\alpha$ pertence ao primeiro quadrante.

Temos que: $\color{NavyBlue}{tg\alpha = {sen\alpha\over cos\alpha}}$

Logo: ${sen\alpha\over cos\alpha} = {4\over3}$$\Leftrightarrow$$sen\alpha = {4\over3}\cdot cos\alpha$

Substituindo na relação fundamental:

$sen^2\alpha + cos^2\alpha = 1$$\Leftrightarrow$$\left({{4\over3}\cdot cos\alpha}\right)^2 + cos^2\alpha = 1$

$\left({{16}\over 9}\right)\cdot cos^2\alpha + cos^2\alpha = 1$$\Leftrightarrow$$\left({{16 + 9}\over 9}\right)\cdot cos^2\alpha = 1$

$cos^2\alpha = {9\over{25}}$$\Leftrightarrow$$\sqrt{cos^2\alpha}=\sqrt{9\over{25}}$

$\color{Maroon}{cos\alpha = {3\over5}}$

Se $sen\alpha = {4\over3}\cdot cos\alpha$$\Leftrightarrow$$sen\alpha = \left({4\over\not{3}}\right)\cdot\left({\not{3}\over5}\right)$

$\color{Maroon}{sen\alpha = {4\over 5}}$

$\color{NavyBlue}{ctg\alpha = {1\over tg\alpha}}$

$ctg\alpha = \left[{1\over\left({4\over3}\right)}\right]$=${3\over4}$

$\color{Maroon}{ctg\alpha = {3\over4}}$

$\color{NavyBlue}{sec\alpha = {1\over cos\alpha}}$

$sec\alpha = \left[{1\over\left({4\over5}\right)}\right]$=${5\over4}$

$\color{Maroon}{sec\alpha = {5\over4}}$

$\color{NavyBlue}{csc\alpha ={1\over sen\alpha}}$

$csc\alpha =\left[{1\over\left({3\over5}\right)}\right]$=${5\over3}$

$\color{Maroon}{csc\alpha = {5\over3}}$

15. Calcular as restantes razões trigonométricas sabendo que o $ cos\alpha={4\over5}$ e $0^{0}< \alpha<90^{0}$, isto é, pertence ao primeiro quadrante.

$\color{NavyBlue}{sen^2\alpha + cos^2\alpha = 1}$

$sen^2\alpha +\left({4\over5}\right)^2 = 1$$\Leftrightarrow$$sen^2\alpha + {{16}\over{25}} = 1$

$sen^2\alpha = {1 – {{16}\over{25}}}$$\Leftrightarrow$$sen^2\alpha = \left({{{25} – {16}}\over{25}}\right)$=${9\over{25}}$

$\sqrt{sen^2\alpha} = \sqrt{9\over{25}}$=${3\over5}$

$\color{Maroon}{sen\alpha = {3\over5}}$

$\color{NavyBlue}{tg\alpha={sen\alpha\over cos\alpha}}$

$tg\alpha = \left[{\left({3\over5}\right)\over\left({4\over5}\right)}\right]$

$tg\alpha = \left({3\over\not{5}}\right)\cdot\left({\not{5}\over4}\right)$

$\color{Maroon}{tg\alpha = {3\over4}}$

$\color{NavyBlue}{ctg\alpha = {cos\alpha\over sen\alpha}}$

$ctg\alpha =\left[{\left({4\over5}\right)\over\left({3\over5}\right)}\right]$

$ctg\alpha = \left({4\over\not{5}}\right)\cdot\left({\not{5}\over3}\right)$

$\color{Maroon}{ctg\alpha = {4\over3}}$

$\color{NavyBlue}{sec\alpha = {1\over cos\alpha}}$

$sec\alpha = \left[{1\over\left({4\over5}\right)}\right]$=${5\over4}$

$\color{Maroon}{sec\alpha = {5\over4}}$

$\color{NavyBlue}{csc\alpha = {1\over sen\alpha}}$

$csc\alpha = \left[{1\over\left({3\over5}\right)}\right]$=${5\over3}$

$\color{Maroon}{csc\alpha={5\over3}}$

Se persistirem algumas dúvidas, não hesite em pedir ajuda. Estou sempre pronto para isso. Se momentaneamente não puder atender, farei isso tão logo seja possível. Obrigado pela consulta.

Curitiba, 08 de janeiro de 2020

Décio Adams

[email protected]  

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

Publicado em

Matemática – Geometria plana – Trigonometria. (Exercícios).

Tabela resumo das relações trigonométricas

Lista das principais relações trigonométricas
$\color{blue}{sen^2\alpha + cos^2\alpha = 1}$
$\color{blue}{tg\alpha = {{sen\alpha}\over cos\alpha}}$
$\color{blue}{ctg\alpha = {{cos\alpha}\over sen\alpha}}$
$\color{blue}{ctg\alpha = {1\over tg\alpha}}$
$\color{blue}{csc\alpha = {1\over sen\alpha}}$
$\color{blue}{sec\alpha = {1\over cos\alpha}}$
$ \color{blue}{csc\alpha = \sqrt{1 + ctg^2\alpha}}$
$ \color{blue}{sec\alpha = \sqrt{1 + tg^2\alpha}}$
$ \color{blue}{cos\alpha = {(1 + tg^2\alpha)}^{-{1\over2}}}$
$ \color{blue}{sen\alpha = {(1 + ctg²\alpha)}^{-{1\over2}}}$
$ \color{blue}{{a\over sen\alpha} = {b\over sen\beta} = {c\over sen\gamma} = 2r}$
$ \color{blue}{a^2 = b^2 + c^2 – 2bc\cdot cos\alpha}$
$ \color{blue}{b^2 = a^2 + c^2 – 2ac\cdot cos\beta}$
$ \color{blue}{c^2 = a^2 + b^2 – 2ab\cdot cos\gamma}$
$ \color{blue}{sen{(\alpha\pm\beta)} = sen\alpha\cdot cos\beta \pm sen\beta\cdot cos\alpha}$
$ \color{blue}{cos{(\alpha\pm\beta)} = cos\alpha\cdot} cos\beta\mp sen\alpha\cdot sen\beta$
$ \color{blue}{tg{(\alpha\pm\beta)}={{1\pm tg\beta\cdot ctg\alpha}\over{ctg\alpha\mp tg\beta}}}$
$ \color{blue}{ctg{(\alpha\pm\beta)} = {{ctg\alpha\mp tg\beta}\over{1\pm tg\beta\cdot ctg\alpha}}}$
$\color{blue}{sec{(\alpha\pm\beta)} = {1\over{cos\alpha\cdot cos\beta\mp sen\beta\cdot sen\alpha}}}$
$\color{blue}{csc{(\alpha\pm\beta)} = {1\over{sen\alpha\cdot cos\beta\pm sen\beta\cdot cos\alpha}}}$
$ \color{blue}{sen{(2\alpha)} = 2\cdot sen\alpha\cdot cos\alpha}$
$ \color{blue}{cos{(2\alpha)} = cos^2\alpha – sen^2\alpha}$
$ \color{blue}{tg{(2\alpha)} = {2\over{ctg\alpha – tg\alpha}}}$
$ \color{blue}{ctg{(2\alpha)} = {{ctg\alpha – tg\alpha}\over 2}}$
$ \color{blue}{csc{(2\alpha)} = {(2sen\alpha\cdot cos\alpha)}^{-{1\over 2}}}$
$ \color{blue}{sec{(2\alpha)} = {(cos^2\alpha – sen^2\alpha)}^{-{1\over 2}}}$

Vamos exercitar.

01. Um dos ângulos agudos de um triângulo tem como $sen\alpha = {\sqrt{5}\over 4}$. Determine: a) o cosseno desse ângulo; b) a tangente e cotangente desse ângulo; c) a secante e cossecante desse ângulo.

a) A relação fundamental nos diz que:

$\color{navy}{sen^2\alpha + cos^2\alpha = 1}$

Se $sen\alpha = {\sqrt{5}\over 4}$, teremos:

${\left(\sqrt{5}\over4\right)}^2 + cos^2\alpha = 1$$\Leftrightarrow$$ {5\over{16}} + cos^2\alpha = 1$

$cos^2\alpha = 1 – {5\over{16}}$$\Leftrightarrow$$cos^2\alpha = {{16 – 5}\over {16}}$

$\sqrt{cos^2\alpha} =\sqrt{{11}\over{16}}$$\Leftrightarrow$$cos\alpha = {\sqrt{11}\over\sqrt{16}}$

$\color{maroon}{cos\alpha = {\sqrt{11}\over 4}}$

b) dispondo do seno e cosseno, podemos facilmente determinar a tangente e cotangente.

$\color{navy}{tg\alpha = {sen\alpha\over cos\alpha}}$

$tg\alpha = \left[\left({\sqrt{5}\over 4}\right)\over\left({\sqrt{11}\over 4}\right)\right]$$\Leftrightarrow$$tg\alpha = {\left(\sqrt{5}\over 4\right)}\cdot{\left(4\over \sqrt{11}\right)}$

$tg\alpha = {{\sqrt{5}}\over{\sqrt{11}}}$$\Leftrightarrow$$tg\alpha = \left({{\sqrt{5}\cdot\sqrt{11}}\over{\sqrt{11}}^2}\right)$

$\color{maroon}{ta\alpha = {\sqrt{55}\over{11}}}$

$\color{navy}{ctg\alpha = {cos\alpha\over sen\alpha}}$

$ctg\alpha = \left[{\left({\sqrt{11}\over 4}\right)\over\left({\sqrt{5}\over 4}\right)}\right]$$\Leftrightarrow$$ctg\alpha = \left[{\left(\sqrt{11}\over 4\right)}\cdot\left({4\over\sqrt{5}}\right)\right]$

$ctg\alpha = \left[{\sqrt{11}\over\sqrt{5}}\right]$$\Leftrightarrow$$ctg\alpha = \left[\left({\sqrt{11}\cdot\sqrt{5}}\right)\over\left({\sqrt{5}}^2\right)\right]$

$\color{maroon}{ctg\alpha = {\sqrt{55}\over 5}}$

c) faltam apenas a secante e cossecante. Isso é fácil.

$\color{navy}{csc\alpha = {1\over sen\alpha}}$

$csc\alpha = \left[{1\over{\left(\sqrt{5}\over 4\right)}}\right]$

$csc\alpha = \left[{\left(4\over\sqrt{5}\right)}\right]$$\Leftrightarrow$$csc\alpha = \left[{\left(4\cdot\sqrt{5}\right)\over{\sqrt{5}^2}}\right]$

$\color{maroon}{csc\alpha = {4\cdot\sqrt{5}\over 5}}$

$\color{navy}{sec\alpha = {1\over cos\alpha}}$

$sec\alpha = \left[{1\over\left({\sqrt{11}\over 4}\right)}\right]$$\Leftrightarrow$$sec\alpha = \left[{\left(4\over\sqrt{11}\right)}\right]$

$sec\alpha = \left[{\left(4\cdot\sqrt{11}\right)\over{\sqrt{11}^2}}\right]$$\Leftrightarrow$$sec\alpha = {4\cdot\sqrt{11}\over 11}$

$\color{maroon}{sec\alpha = {4\cdot\sqrt{11}\over 11}}$

02. Se a $tg\beta = \frac{\sqrt{5}}{5}$, determine a cotangente, a secante e cossecante.

$\color{BlueViolet}{ctg\beta = \frac{1}{tg\beta}}$

$ctg\beta = \left[\frac{1}{\left(\frac{\sqrt{5}}{5}\right)}\right]$$\Leftrightarrow$$ctg\beta = \left[\frac{5}{sqrt{5}}\right]$

$ctg\beta = \left[\left(\frac{5\cdot\sqrt{5}}\right){\sqrt{5}^2}\right]$$\Leftrightarrow$$ctg\beta = \left[\frac{5\cdot \sqrt{5}}{5}\right]$

$\color{Bittersweet}{ctg\beta = \sqrt{5}}$

$\color{navy}{sec\beta = \sqrt{1 + tg^2\beta}}$

$sec\beta =\left[ \sqrt{1 + {\left(\frac{\sqrt{5}}{5}\right)^2}}\right]$$\Leftrightarrow$$sec\beta =\left[\sqrt {1 + \left\(\frac{5}\over{25}\right)}\right]$

$sec\beta = \left[\sqrt{\left({{25} + 5}\right)\over {25}}\right]$$\Leftrightarrow$$sec\beta =\left[\sqrt {{30}\over{25}}\right]$

$\color{Bittersweet}{sec\beta = \frac{\sqrt{30}}{5}}$

$\color{navy}{csc\beta = \sqrt{1 + ctg^2\beta}}$

$csc\beta = \left[\sqrt{1 + \sqrt{5}^2}\right]$$\Leftrightarrow$$csc\beta = \sqrt{1 + 5}$

$\color{Bittersweet}{csc\beta = \sqrt{6}}$

03. Considerando $sen\alpha = {1\over2}$ e $sen\beta = {\sqrt{2}\over2}$, determine: a) $sen{(\alpha + \beta)}$; b) $cos{(\alpha + \beta)}$; c) $tg{(\alpha + \beta)}$; d) $ctg{(\alpha + \beta)}$; e) $sec{(\alpha + \beta)}$; f) $csc{(\alpha + \beta)}$

a) seno de ${(\alpha + \beta)}$

$\color{navy}{sen{(\alpha + \beta)} = {sen\alpha\cdot cos\beta + sen\beta\cdot cos\alpha}}$

Temos que determinar primeiramente o cosseno dos dois ângulos, aplicando a relação fundamental, além da tangente e cotangente.

$\color{navy}{sen^2\alpha + cos^2\alpha = 1}$

$({1\over2})^2 + cos^2\alpha + 1$

${1\over 4} + cos^2\alpha = 1$$\Leftrightarrow$$cos^2\alpha = 1 – {1\over4}$

$cos^2\alpha = {{4 – 1}\over 4}$$\Leftrightarrow$${cos^2\alpha} = {3\over 4}$

$\sqrt{cos^2\alpha} = \sqrt{3\over4}$

$\color{maroon}{cos\alpha = {\sqrt{3}\over 2}}$

$\color{BlueViolet}{sen^2\beta + cos^2\beta = 1}$

$ \left({\sqrt{2}\over 2}\right)^2 + cos^2\beta = 1$$\Leftrightarrow$$ {\not{2}^1\over \not{4}^2} + cos^2\beta = 1$

$cos^2\beta = 1 – {1\over2} = {{2 – 1}\over 2}$

$cos^2\beta = {1\over 2}$$\Leftrightarrow$$\sqrt{cos^2\beta} = \sqrt{1\over{2}}$

$cos\beta = {1\over\sqrt{2}} = {{1\cdot\sqrt{2}}\over{\sqrt{2}}^2}$

$\color{maroon}{cos\beta = {\sqrt{2}\over2}}$

$\color{navy}{tg\alpha = {{sen\alpha}\over{cos\alpha}}}$

$tg\alpha = \left({{1\over 2}\over{\sqrt{3}\over 2}}\right)$$\Leftrightarrow$$tg\alpha = \left({{1\over 2}\cdot{2\over\sqrt{3}}}\right)$=${1\cdot\sqrt{3}\over\sqrt{3}^2}$

$\color{maroon}{tg\alpha = {\sqrt{3}\over 3}}$

$\color{navy}{ctg\alpha = {1\over tg\alpha}}$

$ctg\alpha = \left({1 \over{\sqrt{3}\over 3}}\right)$$\Leftrightarrow$$ctg\alpha = {3\over\sqrt{3}} = {3\sqrt{3}\over{\sqrt{3}^2}}$

$\color{maroon}{ctg\alpha = \sqrt{3}}$

$\color{navy}{tg\beta = {sen\beta\over cos\beta}}$

$tg\beta =\left[{\left({\sqrt{2}\over 2}\right)\over\left({\sqrt{2}\over2}\right)}\right]$

$tg\beta = \left[{\left({\not{\sqrt{2}}^1\over\not{2}^1}\right)\cdot{\left({\not{2}^1\over\not{\sqrt{2}}^1}\right)}}\right]$

$\color{maroon}{tg\beta = 1}$

$\color{navy}{ctg\beta = {1\over tg\beta}}$

$ctg\beta = {1\over 1} = 1$

$\color{maroon}{ctg\beta = 1}$

$\color{blue}{csc\alpha = {1\over sen\alpha}}$

$ csc\alpha = {1\over {1\over 2}}$

$\color{maroon}{csc\alpha = 2}$

$\color{blue}{csc\beta = {1\over{sen\beta}}}$

$ csc\beta = {1 \over{\sqrt{2}\over 2}}$$\Leftrightarrow$$csc\beta = {2\over\sqrt{2}}$

$csc\beta = {2\sqrt{2}\over\sqrt{2}^2}$$\Leftrightarrow$$csc\beta = {2\sqrt{2}\over 2}$

$\color{maroon}{csc\beta = \sqrt{2}}$

$\color{blue}{sec\alpha = {1\over cos\alpha}}$

$sec\alpha = {1\over{\sqrt{3}\over 2}}$$\Leftrightarrow$$sec\alpha = {2\over\sqrt{3}}$

$sec\alpha = {2\cdot\sqrt{3}\over \sqrt{3}^2}$$\Leftrightarrow$$sec\alpha ={2\sqrt{3}\over 3}$

$\color{maroon}{sec\alpha = {2\cdot\sqrt{3}\over 3}}$

$\color{blue}{sec\beta = {1\over cos\beta}}$

$sec\beta = {1\over{\sqrt{2}\over 2}}$$\Leftrightarrow$$sec\beta = {2\over \sqrt{2}}$

$sec\beta = {2\cdot \sqrt{2}\over\sqrt{2}^2}$$\Leftrightarrow$$sec\beta = {2\sqrt{2}\over 2}$

$\color{maroon}{sec\beta = \sqrt{2}}$

$sen{(\alpha + \beta)} = {{1\over2}\cdot{\sqrt{2}\over 2}} + {{\sqrt{2}\over 2}\cdot {\sqrt{3}\over2}}$

$sen{(\alpha + \beta)} = {\sqrt{2}\over 4} + {\sqrt{6}\over 4}$

$\color{maroon}{sen{(\alpha + \beta)} = {{\sqrt{2} + \sqrt{6}}\over 4}}$

b) cosseno de ${(\alpha + \beta)}$

$cos{(\alpha + \beta)} = {{\sqrt{3}\over 2}\cdot {\sqrt{2}\over 2} – {{1\over2}\cdot {\sqrt{2}\over 2}}}$

$cos{(\alpha + \beta)} = {{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}$

$\color{maroon}{cos{(\alpha + \beta)} = {{\sqrt{6} – \sqrt{2}}\over4}}$

c) tangente de ${(\alpha + \beta)}$

$ \color{marine}{tg{(\alpha\pm\beta)}={{1\pm tg\beta\cdot ctg\alpha}\over{ctg\alpha\mp tg\beta}}}$

$tg{(\alpha + \beta)} = {{1 + {1\cdot\sqrt{3}}}\over{{\sqrt{3} – 1}}}$

$tg{(\alpha + \beta)} =\left[{\left({{1 + \sqrt{3}}}\right)\over\left({\sqrt{3} -1}\right)}\right]$

Racionalizando o denominador:

$tg{(\alpha + \beta)} = \left[{\left({\sqrt{3} + 1}\right)\over\left({\sqrt{3} – 1}\right)}\right]\cdot\left[{\left({\sqrt{3} + 1}\right)\over\left({\sqrt{3} + 1}\right)}\right]$

$tg{(\alpha + \beta)} = \left[{\left({\sqrt{3}^2 + 2\sqrt{3} + 1}\right)\over\left({\sqrt{3}^2 – 1^2}\right)}\right]$$\Leftrightarrow$$tg{(\alpha + \beta)} = \left[{\left({3 + 2\sqrt{3} + 1}\right)\over\left({3 – 1}\right)}\right]$

$tg{(\alpha + \beta)} = \left[{{2\sqrt{3} + 4}\over{2}}\right]$

$\color{maroon}{tg{(\alpha + \beta)} = {\sqrt{3} + 2}}$

d) cotangente de ${(\alpha + \beta)}$

$\color{navy}{ctg{(\alpha + \beta)}= \left({{ctg\alpha – tg\beta}\over{1 + tg\beta\cdot ctg\alpha}}\right)}$

$ctg{(\alpha + \beta)} =\left[{\left({\sqrt{3} – 1}\right)\over{1 + \left({1\cdot\sqrt{3}}\right)}}\right]$$\Leftrightarrow$$ctg{(\alpha + \beta)} = \left[{{(\sqrt{3} – 1)}\cdot{(\sqrt{3} – 1)}\over{(\sqrt{3} + 1)}\cdot {(\sqrt{3} – 1)}}\right]$

$ctg{(\alpha + beta)} = \left[{{(\sqrt{3} – 1)}^2\over{(\sqrt{3}^2 – 1^2)}}\right]$$\Leftrightarrow$$ctg{(\alpha + \beta)} = \left[{
{(3 – 2\sqrt{3} +1)}\over 2}\right]$

$ctg{(\alpha + \beta)} = \left({{4 – 2\sqrt{3}}\over 2}\right) = {2 -\sqrt{3}}$

$\color{maroon}{ctg{(\alpha + \beta)} = {2 – \sqrt{3}}}$

e)secante ${(\alpha + \beta)}$

$\color{navy}{sec{(\alpha + \beta)} = \left[{{1} \over\left({{cos\alpha\cdot cos\beta} – {sen\alpha\cdot sen\beta}}\right)}\right]}$

$sec{(\alpha + \beta)} = \left[{{1}\over\left({{{\sqrt{3}\over 2}\cdot{\sqrt{2}\over 2}} – {{1\over 2}\cdot {\sqrt{2}\over 2}}}\right)}\right]= \left[{{1}\over\left({{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}\right)}\right]$*

$sec{(\alpha + \beta)} = \left({{4}\over{\sqrt{6} – \sqrt{2}}}\right)$=$\left[{{4\cdot\left({\sqrt{6} + \sqrt{2}}\right)}\over{\left({\sqrt{6} – \sqrt{2}}\right)}\cdot\left({\sqrt{6} + \sqrt{2}}\right)}\right]$

$sec{(\alpha + \beta)} = \left[{{4\cdot\left({\sqrt{6} + \sqrt{2}}\right)}\over\left({6 – 2}\right)}\right] = \left[{{4\cdot\left({\sqrt{6} + \sqrt{2}}\right)}\over 4}\right]$

$\color{maroon}{sec{(\alpha + \beta)} = {\sqrt{6} + \sqrt{2}}}$

f) cossecante de ${(\alpha + \beta)}$

$\color{navy}{csc{(\alpha + \beta)} = \left({{1}\over{{sen\alpha\cdot cos\beta} + {sen\beta\cdot cos\alpha}}}\right)}$

$csc{(\alpha + \beta)} = \left[{{1}\over\left({{1\over 2}\cdot {\sqrt{2}\over 2} + {\sqrt{2}\over 2}\cdot{\sqrt{3}\over 2}}\right)}\right]$=$\left[{{1}\over\left({{\sqrt{2}\over 4} + {\sqrt{6}\over 4}}\right)}\right]$

$csc{(\alpha + \beta)} = \left[{{1}\over\left({{\sqrt{2} + \sqrt{6}}\over 4}\right)}\right]$=$\left[{{4}\over\left({\sqrt{2} + \sqrt{6}}\right)}\right]$

$csc{(\alpha + \beta)} = \left[{{4\cdot\left({\sqrt{2} – \sqrt{6}}\right)}\over\left({\sqrt{2} + \sqrt{6}}\right)\cdot\left({\sqrt{2} – \sqrt{6}}\right)}\right]$=$\left[{{4\cdot\left({\sqrt{2} – \sqrt{6}}\right)}\over\left({2 – 6}\right)}\right]$

$csc{(\alpha + \beta)} = \left[{{4\cdot\left({\sqrt{2} – \sqrt{6}}\right)}\over {- 4}}\right]$=$\left[{{\sqrt{2} – \sqrt{6}}\over {-1}}\right]$

$\color{maroon}{csc{(\alpha + \beta)} = {\sqrt{6} – \sqrt{2}}}$

04. Sabe-se que $\color{blue}{cos\alpha ={1\over 2}}$ e $\color{blue}{sen\beta ={\sqrt{2}\over 2}}$. Determine: a) $\color{blue}{sen{(\alpha – \beta)}}$; b) $\color{blue}{cos{(\alpha – \beta)}}$; c) $\color{blue}{tg{(\alpha – beta)}}$; d)$\color{blue}{ctg{(\alpha – beta)}}$; e)$\color{blue}{csc{(\alpha – beta)}}$ e $\color{blue}{sec{(\alpha – beta)}}$.

Novamente começaremos por determinar o seno e o cosseno de $\alpha$ e $\beta$.

Temos que: $\color{brown}{cos\alpha = {1\over 2}}$

$\color{blue}{sen²\alpha + cos²\alpha = 1}$

Substituímos: $sen^2\alpha + {\left(1\over 2\right)}^2 = 1$$\Leftrightarrow$$sen^2\alpha + {1\over 4} = 1$

$sen^2\alpha = {1 – {1\over 4}}$$\Leftrightarrow$$sen^2\alpha = {3\over 4}$

$\sqrt{sen^2\alpha} = \sqrt{3\over 4}$$\Leftrightarrow$$sen\alpha ={\sqrt{3}\over\sqrt{4}}$

$\color{maroon}{sen\alpha = {\sqrt{3}\over 2}}$

Temos também que: $\color{blue}{sen\beta = {\sqrt{2}\over2}}$

Substituindo na relação fundamental: $\color{navy}{sen^2\beta + cos^2\beta = 1}$

$\left({\sqrt{2}\over 2}\right)^2+ cos^2\beta = 1$

$\left({\not{2}^1\over\not{4}^2}\right) + cos^2\beta = 1$$\Leftrightarrow$$cos^2\beta = {1 – {1\over 2}}$

$\sqrt{cos^2\beta} = {\sqrt{1\over 2}}$$\Leftrightarrow$$cos\beta = {\sqrt{1}\over\sqrt{2}}$

$cos\beta = {1\over\sqrt{2}}= {1\cdot\sqrt{2}\over\sqrt{2}^2}$

$\color{maroon}{cos\beta = {\sqrt{2}\over2}}$

Agora podemos determinar:

$\color{blue}{sen{(\alpha – \beta)} = {sen\alpha\cdot cos\beta – sen\beta\cdot cos\alpha}}$

$sen{(\alpha – \beta)}={{\sqrt{3}\over2}\cdot{\sqrt{2}\over2} – {\sqrt{2}\over 2}\cdot{1\over 2}}$=${{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}$

$\color{maroon}{sen{(\alpha – \beta)} = {{\sqrt{6} -\sqrt{2}}\over 4}}$

b)Também podemos determinar$\color{brown}{cos{(\alpha – \beta)}}$.

$\color{navy}{cos{(\alpha – \beta)} = {{cos\alpha\cdot cos\beta} + {sen\alpha\cdot sen\beta}}}$

$cos{(\alpha – \beta)} = {({1\over2})\cdot({\sqrt{2}\over 2})+({\sqrt{3}\over2})\cdot({\sqrt{2}\over 2})}$=${({\sqrt{2}\over4}) + ({\sqrt{6}\over 4})}$

$\color{maroon}{cos{(\alpha – \beta)} = {{\sqrt{2} + \sqrt{6}}\over 4}}$

c) Vamos determinar $\color{blue}{tg{(\alpha – \beta)}}$

Começaremos por determinar:

$\color{blue}{tg\alpha}$; $\color{blue}{tg\beta}$; $\color{blue}{ctg\alpha}$ e $\color{blue}{ctg\beta}$

$\color{blue}{tg\alpha = {{sen\alpha}\over {cos\alpha}}}$

$tg\alpha = \left[{\left({\sqrt{3}\over 2}\right)\over\left({1\over2}\right)}\right]$$\Leftrightarrow$$tg\alpha = \left[{\left({\sqrt{3}\over2}\right)\cdot\left({1\over2}\right)}\right]$

$\color{maroon}{tg\alpha = {\sqrt{3}\over 4}}$

$\color{blue}{tg\beta = \left[{\left({sen\beta}\right)\over\left({cos\beta}\right)}\right]}$

$tg\beta =\left[{\left({\sqrt{2}\over 2}\right)\over\left({\sqrt{2}\over2}\right)}\right]$

$\color{maroon}{tg\beta = 1}$

$\color{blue}{ctg\alpha = {cos\alpha\over sen\alpha}}$

$ctg\alpha = \left[{\left({1\over2}\right)\over\left({\sqrt{3}\over2}\right)}\right]$ $\Leftrightarrow$$ ctg\alpha = \left[{\left({1\over 2}\right)\cdot\left({2\over \sqrt{3}}\right)}\right]$

$ctg\alpha = \left[{\left({1\cdot\not{2}}\right)\over\left({\not{2}\cdot\sqrt{3}}\right)}\right]$$\Leftrightarrow$$ctg\alpha = {1\over\sqrt{3}} = {{1\cdot\sqrt{3}}\over\sqrt{3}^2}$

$\color{maroon}{ctg\alpha = {\sqrt{3}\over 3}}$

$\color{navy}{ctg\beta ={{cos\beta}\over{sen\beta}}}$

$ctg\beta = \left[{\left({\sqrt{2}\over 2}\right)\over\left({\sqrt{2}\over 2}\right)}\right]$

$\color{maroon}{ctg\beta = 1}$

$\color{blue}{tg{(\alpha – \beta)} = \left[{\left({1 – tg\beta\cdot ctg\alpha}\right)\over\left({ctg\alpha + tg\beta}\right)}\right]}$

$tg{(\alpha – \beta)} =\left[{{1 + \left({1\cdot\sqrt{3}\over 3}\right)}}\over{\left({{\sqrt{3}\over 3} + 1}\right)}\right]$$\Leftrightarrow$$tg{(\alpha – \beta)} = \left[{{\left({1 + \sqrt{3}}\right)\over3}\over{\left({\sqrt{3}\over3} + 1}\right)}}\right]$

$tg{(\alpha – \beta)}=\left[{\left({{3 + \sqrt{3}}\over\not{3}}\right)\cdot\left({\not{3}\over\sqrt{3}}\right)}\right]$$\Leftrightarrow$$tg{(\alpha – \beta)} = \left[{{\left({3 +\sqrt{3}}\right)\cdot\sqrt{3}}\over{\sqrt{3} +{3}}}\right]$=$\left[{{3\sqrt{3} +\sqrt{3}^2}\over\sqrt{3}^2}\right]$

$tg{(\alpha – \beta)}=\left[{{3\sqrt{3} + 3}\over 3}\right]={\sqrt{3} + 1}$

$\color{maroon}{tg{(\alpha – \beta)} = {\sqrt{3} + 1}}$

d) Agora a cotangente $\color{blue}{(\alpha – \beta)}$

$ \color{blue}{ctg{(\alpha\pm\beta)} = {{ctg\alpha\mp tg\beta}\over{1\pm tg\beta\cdot ctg\alpha}}}$

$ctg{(\alpha – \beta)}=\left[{\left({{\sqrt{3}\over3} + 1}\right)\over\left({1 – 1\cdot{\sqrt{3}\over3}}\right)}\right]$=$\left[{\left({{\sqrt{3} + 3}\over3}\right)\over\left({{3 -\sqrt{3}}\over3}\right)}\right]$

$ctg{(\alpha -\beta)} = \left[{\left({{\sqrt{3} + 3}\over\not{3}}\right)\cdot\left({\not{3}\over{\sqrt{3} – 3}}\right)}\right]$

$ctg{(\alpha – \beta)}=\left[{({\sqrt{3} +3})\cdot({\sqrt{3} + 3})\over({\sqrt{3}-3})\cdot({\sqrt{3}+3})}\right]$

$ctg{(\alpha-\beta)}=\left[{({\sqrt{3}^2 + 6\cdot\sqrt{3} + 9})\over({\sqrt{3}^2 – 9})}\right]$

$ctg{(\alpha – \beta)} = {{12 + 6\sqrt{3}}\over{3 – 9}}$=${{12 + 6\sqrt{3}}\over{-6}}$

$\color{maroon}{ctg{(\alpha-\beta)} = {\sqrt{3} – 2}}$

e) Vamos à secante $\color{blue}{(\alpha-\beta)}$

$\color{blue}{sec{(\alpha\pm\beta)} = {1\over{cos\alpha\cdot cos\beta\mp sen\beta\cdot sen\alpha}}}$

$sec{(\alpha-\beta)}=\left[{1\over{{1\over2}\cdot{\sqrt{2}\over2} +{\sqrt{3}\over2}\cdot {\sqrt{2}\over2}}}\right]$=$\left[{1\over{{\sqrt{2}\over4}+{\sqrt{6}\over4}}}\right]$

$sec{(\alpha-\beta)}=\left({4\over{\sqrt{2} + \sqrt{6}}}\right)$=$\left[{4\cdot\left({\sqrt{2}-\sqrt{6}}\right)\over{\left({\sqrt{2} +\sqrt{6}}\right)\cdot\left({\sqrt{2} -\sqrt{6}}\right)}}\right]$

$sec{(\alpha-\beta)}=\left[{4\cdot\left({\sqrt{2} -\sqrt{6}}\right)\over\left({\sqrt{2}^2 – \sqrt{6}^2}\right)}\right]$=$\left[{4\cdot\left({\sqrt{2} -\sqrt{6}}\right)\over{2 – 6}}\right]$

$sec{(\alpha-\beta)}=\left[{\not{4}\cdot\left({\sqrt{2} – \sqrt{6}}\right)\over {-\not{4}}}\right]$=${-{\left(\sqrt{2} – \sqrt{6}\right)}}$

$\color{maroon}{sec{(\alpha-\beta)} = {\sqrt{6} – \sqrt{2}}}$

f) é a vez da cossecante $\color{blue}{(\alpha-\beta)}$

$\color{navy}{csc{(\alpha-\beta)}=\left({1\over{sen\alpha\cdot cos\beta – sen\beta\cdot cos\alpha}}\right)}$

$csc{(\alpha-\beta)}=\left[{1\over\left({{\sqrt{3}\over2}\cdot{\sqrt{2}\over2}}-{{\sqrt{2}\over2}\cdot{1\over2}}\right)}\right]$=$\left[{1\over\left({{\sqrt{6}\over 4} – {\sqrt{2}\over 4}}\right)}\right]$

$csc{(\alpha-\beta)}=\left[{1\over\left({{\sqrt{6} – \sqrt{2}}\over4}\right)}\right]$=$\left[{4\over{\sqrt{6} -\sqrt{2}}}\right]$

$csc{(\alpha-\beta)}=\left[{4\cdot\left({\sqrt{6}+\sqrt{2}}\right)\over\left({\sqrt{6} – \sqrt{2}}\right)\cdot\left({\sqrt{6}+\sqrt{2}}\right)}\right]$

$csc{(\alpha-\beta)}=\left[{4\cdot\left({\sqrt{6}+\sqrt{2}}\right)\over\left({6 – 2}\right)}\right]$=$\left[{4\cdot\left({\sqrt{6} +\sqrt{2}}\right)\over 4}\right]$

$\color{maroon}{csc{(\alpha-\beta)}={\sqrt{6} +\sqrt{2}}}$

05. Sabe-se que um ângulo tem $sen\gamma={\sqrt{6}\over5}$. Determine: a) $sen{2\gamma}$; b)$cos{2\gamma}$; c)$tg{2\gamma}$; d)$ctg{2\gamma}$

a) Seno do ângulo duplo $\color{green}{sen{2\gamma}}$

Precisamos começar determinando o cosseno do ângulo.

$\color{navy}{sen²\gamma + cos²\gamma = 1}$

$({\sqrt{6}\over 5})² + cos²\gamma = 1$$\Leftrightarrow$${6\over25} + cos²\gamma = 1$

$cos²\gamma = 1 – {6\over{25}}= {{25 -6}\over25}$

$\sqrt{cos²\gamma} = {\sqrt{{19}\over{25}}}$

$\color{blue}{cos\gamma = {\sqrt{19}\over5}}$

$\color{navy}{sen{(2\gamma)}= {2\cdot sen\gamma\cdot cos\gamma}}$

$sen{(2\gamma)}={2\cdot \left({\sqrt{6}\over 5}\right)\cdot\left({\sqrt{19}\over 5}\right)}$

$sen{(2\gamma)}= {2\cdot\left({\sqrt{114}\over{25}}\right)}$

$\color{maroon}{sen{(2\gamma)}= {2\sqrt{114}\over25}}$

b)$cos{(2\gamma)}$

$\color{navy}{cos{(2\gamma)}={cos^2\gamma – sen^2\gamma}}$

$cos{(2\gamma)}={\left({\sqrt{19}\over 5}\right)^2 – \left({\sqrt{6}\over 5}\right)^2}$

$cos{(2\gamma)}={{{19}\over{25}} – {6\over{25}}}={{13}\over{25}}$

$\color{maroon}{cos{(2\gamma)}={{13}\over{25}}}$

c)$\color{green}{tg{(2\gamma)}}$

Comecemos por determinar a $\color{red}{tg\gamma}$ e $\color{red}{ctg\gamma}$

$\color{blue}{tg\gamma = {{sen\gamma}\over {cos\gamma}}}$

$tg\gamma = \left[{({\sqrt{6}\over 5})\over({\sqrt{19}\over 5})}\right]$=$\left[{({\sqrt{6}\over \not{5}})\cdot({\not{5}\over\sqrt{19}})}\right]$

$tg{\gamma}=\left[{{\sqrt{6}\cdot\sqrt{19}}\over{\sqrt{19}\cdot\sqrt{19}}}\right]$= ${\sqrt{114}\over{19}}$

$\color{maroon}{tg\gamma = {\sqrt{114}\over{19}}}$

$\color{blue}{ctg\gamma = {1\over tg\gamma}}$

$ctg\gamma = \left[{1\over{\sqrt{114}\over{19}}}\right]$=$\left[{{19}\over\sqrt{114}}\right]$

$ctg\gamma=\left[{({19}\cdot\sqrt{114})\over({\sqrt{114}\cdot\sqrt{114}})}\right]$=$\left[{({{19}\cdot\sqrt{114}})\over{114}}\right]$

$\color{maroon}{ctg{(\gamma)}={\sqrt{114}\over 6}}$

$\color{navy}{tg{(2\gamma)}= {2\over{ctg\gamma – tg\gamma}}}$

$tg{(2\gamma)}=\left[{2\over{\left({\sqrt{114}\over 6}\right)-\left({\sqrt{114}\over{19}}\right)}}\right]$=$\left[{2\over\left({{{19}\sqrt{114} – 6\sqrt{114}}\over{114}}\right)}\right]$

$tg{(2\gamma)}=\left[{({2\cdot{114}})\over({{113}\cdot\sqrt{114}})}\right]$=$\left[{\left(2\cdot{114}\sqrt{114}\right)\over\left({113\sqrt{\left(114\right)}²}\right)}\right]$

$\color{maroon}{tg{(2\gamma)}= {2\sqrt{114}\over {113}}}$

d)$\color{green}{ctg{(2\gamma)}}$

$\color{blue}{ctg{(2\gamma)}={1\over tg{(2\gamma)}}}$

$ctg{(2\gamma)}=\left[{1\over({2\sqrt{114}\over {113}})}\right]$=$\left[{{113}\sqrt{114}\over{2\sqrt{114}^2}}\right]$

$ctg{(2\gamma)}=\left[{{{113}\sqrt{114}}\over 228}\right]$

$\color{maroon}{ctg{(2\gamma)}={{113}\sqrt{114}\over{228}}}$

Exercícios para treinar

01. Se um triângulo isósceles tem o ângulo oposto à base, medindo $\alpha = 60º$, determine o seno e o cosseno do ângulo resultante da justaposição de dois desses triângulos, como mostra a figura.

02. Sabendo que um ângulo $\beta$ mede mede 30º e o outro mede 45º. Determine a tangente e cotangente da soma desses dois ângulos.

Triângulos contíguos, com um vértice comum.

03. Dois triângulos são colocados lado a lado, de modo a fazer coincidir um de seus vértices da base. O primeiro é equilátero e o segundo isósceles, onde o ângulo do vértice superior mede 45º. Determine: a) o seno do ângulo entre os lados dos dois triângulos $\color{red}{\alpha}$; b) o cosseno da soma do ângulo interno do equilátero e o lado do isósceles$\color{red}{(\alpha + \gamma)}$; c) o seno do ângulo formado entre a base do isósceles e o lado do equilátero$\color{red}{(\alpha + \beta)}$.

05. Sendo os ângulos $\color{red}{\alpha = 60º}$ e $\color{red}{\beta = 45º}$, determine: a) $cos{(\alpha – \beta)}$; b)$sen{(\alpha – \beta)}$; c)$tg{(\alpha – \beta)}$.

06. Calcular as restantes razões trigonométricas sabendo que tgα=4/3 e α pertence ao primeiro quadrante($0\lt\alpha\lt90^{0}$.

07. Demostrar as seguintes igualdades trigonométricas:

a)$\left[{{1 – sen\alpha}\over cos\alpha}\right] = \left[{{cos\alpha}\over{1 + sen\alpha}}\right]$;

b) $\left[{{sen\alpha + ctg\alpha}\over{tg\alpha + cosec\alpha}}\right] = cos\alpha$;

c)${tag\alpha + ctg\alpha} = sec\alpha\cdot csec\alpha$;

d)$cos^2\alpha = sen^2\alpha\cdot cos^2\alpha + cos^4\alpha$

08. Faça a demonstração das igualdades trigonométricas:

a)$\color{blue}{2tg x\left({{1 + cos x}over 2}\right)} = sen x\cdot tg x$

b)$\color{blue}{\left({{tg\alpha + tg\beta}\over{ctg\alpha +ctg\beta}}\right) = tg\alpha\cdot tg\beta}$

09. Demonstrar as seguintes igualdades trigonométricas.

a)$\color{blue}{sec^2\alpha + csc^2\alpha = sec^2\alpha\cdot csc^2\alpha}$

b)$\color{blue}{\left({{sen\alpha\cdot cos\alpha}\over{sen^2\alpha -cos^2\alpha}}\right) = sec^2\alpha\ cdot csc^2\alpha}$

c)$\color{blue}{{\left(sec\alpha – tg\alpha\right)^2 }=\left({{1-sen\alpha}\over{1+sen\alpha}}\right)}$

10. Demonstre as seguintes identidades trigonométricas.

a)$\color{blue}{sen\alpha + cos\alpha = \left({{1 + tg\alpha}\over{sec\alpha}}\right)}$

b)$\color{blue}{\left({{cos\alpha + tg\alpha}\over{cos\alpha\cdot tg\alpha}}\right) = ctg\alpha + sec\alpha}$

c)$\color{blue}{\left({{2sen\alpha}\over{tg(2\alpha)}}\right) = cos\alpha – \left({sen²\alpha\over cos\alpha}\right)}$

11. Demonstrar as seguintes igualdades trigonométricas.

a)$\color{blue}{1 + sen\alpha\cdot tg\alpha = \left({{sen\alpha + ctg\alpha}\over{ctg\alpha}}\right)}$

b)$\color{blue}{tg\alpha + ctg\alpha = \left({1\over{sen\alpha\cdot cos\alpha}}\right)}$

c)$\color{blue}{{\left(sen\alpha + cos\alpha\right)^2} +{\left(sen\alpha – cos\alpha\right)^2} = 2}$

12. Calcular as restantes razões trigonométricas sabendo que $ sen\alpha=3/5 $ e $0\lt\alpha\lt90$, isto é pertence ao primeiro quadrante.

13. Calcular as outras razões trigonométricas sabendo que o $cos\alpha=5/13$ e $ \alpha$ pertence ao primeiro quadrante.

14. Calcular as outras razões trigonométricas sabendo que $ tgα=4/3$ e $α$ pertence ao primeiro quadrante.

15. Calcular as demais razões trigonométricas sabendo que o $\color{Green}{ cos\alpha={4\over 5}}$ e $0< α<90^{0}$, isto é, pertence ao primeiro quadrante.

Irá seguir em pouco tempo um post com a resolução de todos esses exercícios para que possas conferir e tirar dúvidas.

Curitiba, 30 de dezembro de 2019

Décio Adams

[email protected]  

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732