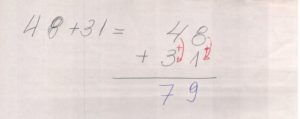Adição de números naturais
Números com vários algarismos. Mais de dois números.
Vamos ver agora como se procede com mais de dois números. Sejam os números.
- 35 + 21 + 43 =
3 5
+ 2 1
4 3
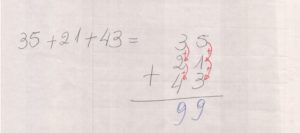
9 9
Temos na coluna das unidades simples (5 + 1 + 3 = 9) e na coluna das dezenas (3 + 2 + 4 = 9). Escrevemos os dois resultados abaixo das colunas correspondentes, sob a reta horizontal e temos o resultado da adição, que dá noventa e nove (99). São nove dezenas e nove unidades simples.
- 413 + 324 + 252 =
4 1 3
+ 3 2 4
2 5 2
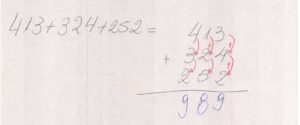
9 8 9
Na coluna das unidades temos (3 + 4 + 2 = 9), na coluna das dezenas (1 + 2 + 5 =8) e na coluna das cebtebas simples temos ( + 4 + 3 + 2 = 9). Escrevendo os resultados abaixo das colunas correspondentes, teremos o resultado da adição que é 989. Nove centenas, oito dezenas e nove unidades simples. Facilmente entendemos que se houver mais números a serem adicionados, bastará escreve-los todos na forma de colunas e efetuar a adição, começando da direita (unidades) para esquerda. Novamente iremos exercitar o que vimos.
Efetue as adições, escrevendo em colunas os números (parcelas).
- 17 + 42 + 30 =
- 43 + 12 + 34 =
- 132 + 225 + 312 =
- 315 + 462 + 212 =
- 3125 + 2423 + 1321 =
- 1473 + 3012 + 4114 =
- 132 + 205 + 230 + 322 =
- 92 + 142 + 231 + 420 + 23 =
Realize as adições e confira, revisando para ter certeza de que o resultado é o que você encontrou. Se tiver dúvidas, entre em contato comigo por um dos canais abaixo listados.
Curitiba, 18 de julho de 2018
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/adamsdecio
Telefone: (41) 3019-4760
Celulares: (41) 99805-0732