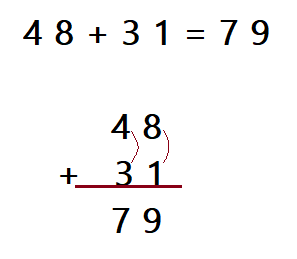Aritmética.
Essa palavra designa a parte da Matemática que nos apresenta ao mundo dos números. Começamos por aprender a contar, associar um símbolo aos números que correspondem às quantidades de objetos que contamos. Esses símbolos denominamos algarismos, e os mais usados no mundo hoje em dia são os hindu arábicos. Essa denominação é devida ao fato de sua origem ter ocorrido na India e depois foram aperfeiçoados na Arábia. Depois de dominarmos a escrita e leitura dos números, fazendo o uso adequado da posição dos algarismos, começamos a aprender as quatro operações:
-
Adição
Consiste na reunião dos elementos de dois ou mais conjuntos. A quantidade de elementos resultante é denominada soma. A soma será o número de elementos do novo conjunto formado pela reunião dos primeiros. Por exemplo. Seja o conjunto $\color{Navy}{A =\varnothing}$ e $\color{Navy}{B = \{ O\}}$. O primeiro conjunto é vazio, isto é não tem nenhum elemento. Então o número de elementos é $\color{Navy}{n(A) = 0}$. O segundo conjunto tem apenas uma letra “O“. Portanto $\color{Navy}{n(B) = 1}$. Vamos representar isso num desenho.
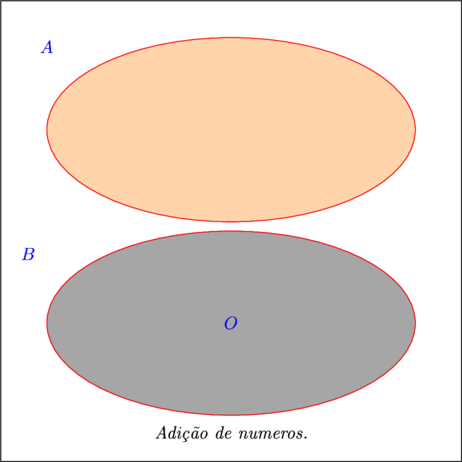
- Vamos reunir os elementos dos dois conjuntos em um único conjunto e contar a quantidade de elementos resultante.
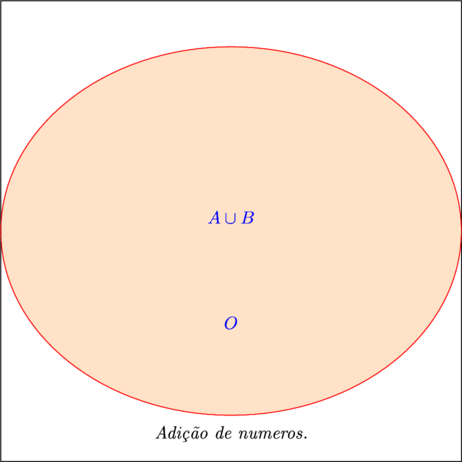
- Notamos que da reunião dos dois conjuntos resultou um novo conjunto com um único elemento. Isto nos permite afirmar que a adição dos números 0 (zero) com o número 1(um), resulta na soma 1 (um). Ou seja adicionar 0 (zero) com qualquer número não altera o resultado.
- $\color{Navy}{0 + 1 = 1}$
- Vejamos agora dois conjuntos, tendo o primeiro 1(um) elemento e o outro 2(dois) elementos. Façamos a reunião dos mesmos e vejamos quantos elementos resultam.
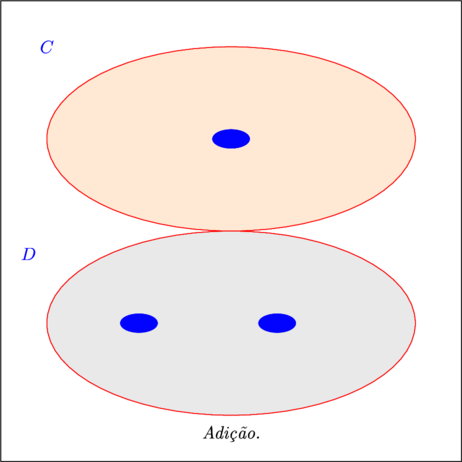
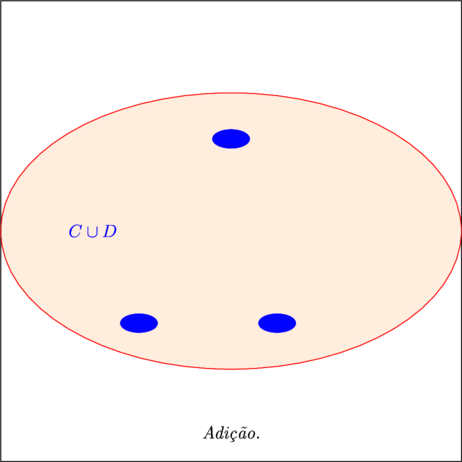
- Notamos que o conjunto que reúne os dois conjuntos é um conjunto com um total de 3(três) elementos. Portanto:
- $\color{Navy}{ 1 + 2 = 3 }$
- Este procedimento de juntar os elementos de dois ou mais conjuntos você pode fazer usando os dedos de suas mãos. Vejamos mais um exemplo. Um conjunto M com três elementos e um conjunto N com quatro elementos.
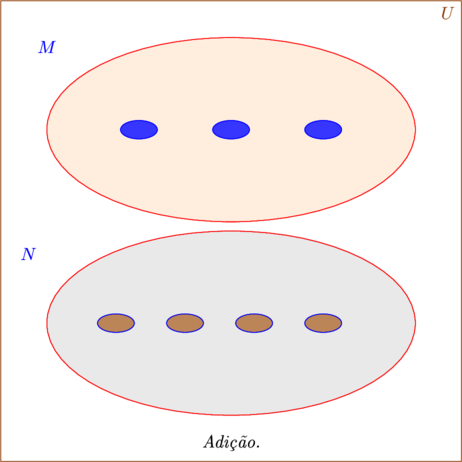
Vemos na figura dois conjuntos com o mesmo tipo de elementos. O conjunto M formado por três elipses e o conjunto N por 4 elipses. Podemos reunir todos em um único conjunto e ver quantos serão os elementos do do novo conjunto formado pela reunião dos dois.
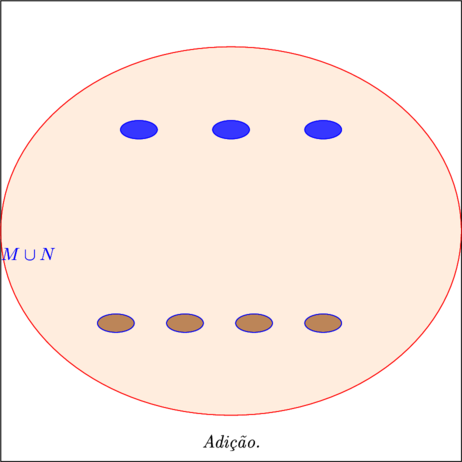
Se contarmos o número de elementos existentes no novo conjunto encontraremos como resultado o número 7. Isto nos permite afirmar que a adição dos números que representam a quantidade de elementos dos dois conjuntos que foram reunidos, tem como resultado 7 (sete). Simbolicamente fica:
- $\color{Navy}{ 3 + 4 = 7} $
- Se você quiser fazer a adição de 5 ovos com 7 ovos, usando os dedos das mãos, como irá proceder?
- Em condições normais, você terá em sua mão esquerda 5 dedos, que podem representar os 5 ovos. Na outra mão terá também 5 dedos, que poderão representar outros 5 ovos. Se você continuar contando, depois do cinco vem o seis e logo o sete. Portanto faltarão dois dedos. Conte os dedos da mão esquerda, os da mão direita, chegando a 10, e volte a contar mais dois da mão esquerda. Deverá obter o número 12. Ou seja:
- $\color{Navy}{ 5 + 7 = 5 + 5 + 2 = 12 }$
- 6 uvas + 3 maçãs = 9 frutas, mas não serão 9 uvas, nem 9 maçãs. Em geral não adicionamos coisas diferentes.
- Os números que somamos são chamados parcelas. O número de parcelas de uma adição, não tem limites e nem importa a ordem em que as adicionamos, contanto que façamos o processo de maneira correta.
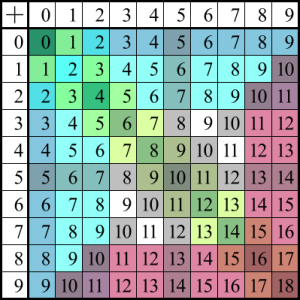
- A tabela apresentada acima, pode ser útil para obter a soma da adição de números entre 0(zero) e 9 (nove). Pode substituir os dedos ou outros objetos no momento de realizar a adição de números.
-
Adição de números maiores.
- Sejam, por exemplo as parcelas $\color{Navy}{ 149 + 214 = ?}$
- Eles serão escritos um sobre o outro, formando a coluna das unidades, a coluna das dezenas, centenas, milhares e assim até o final. Começamos a efetuar pelas unidades e assim sucessivamente, até completar a adição. O número formado será a soma das parcelas.
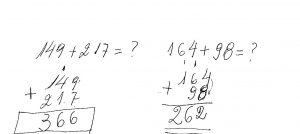
- Na figura ao lado, vemos efetuada a adição dos dois números dados. Observe que adicionamos a partir das unidades. No caso $\color{Navy}{ 9 + 7 = 16}$. Escrevemos as unidades 6 (seis) abaixo da linha horizontal e a dezena, colocamos acima do 4 (quatro), na coluna das dezenas. Repetimos o processo e obtemos $\color{Navy}{1 + 4 + 1=6}$ (seis) dezenas. Não temos nenhuma centena. Adicionamos a coluna das centenas e resulta a soma $\color{Navy}{366}$.
- Ao lado temos a adição $\color{Navy}{164 + 98 = ?}$. Na formação das colunas, a casa das centenas ficou vaga para o segundo número, uma vez que temos um número sem nenhuma centena. $\color{Navy}{4 + 8 = 12}$, nos dá duas unidades e uma dezena. Escrevemos as duas unidades abaixo da linha horizontal e a dezena colocamos acima dos algarismos das dezenas. Somamos $\color{Navy}{ 1 + 6 + 9 = 16}$ que nos dá seis dezenas de unidades e uma centena. O seis vai ao lado do dois, na casa das dezenas e a centena, acima dos algarismos das centenas. Somamos $\color{Navy}{1 + 1 = 2}$, resultam duas centenas e a soma dos números é igual a $\color{Navy}{262}$.
- Tomemos mais dois exemplos.
- $\color{Navy}{1537 + 7259 = ? }$
- $\color{Navy}{2836 + 475 =?}$

- Note que devemos colocar os algarismos na posição correta e sempre efetuar a adição da direita (unidades) para esquerda, seguindo a ordem das dezenas, centenas e demais classes. A adição de $\color{Navy}{7 + 9 = 16}$. Seis unidades e uma dezena que irá ser adicionada na segunda coluna. Assim $\color{Navy}{1 + 3 + 5 = 9}$. Escrevemos as nove dezenas na segunda coluna, ao lado esquerdo das seis unidades da primeira coluna. Adicionamos $\color{Navy}{5 + 2 = 7}$ e depois $\color{Navy}{1 + 7 = 8}$. O resultado (soma) será o número ${8796}$. Procedemos da mesma maneira com os outros dois números.
-
Vamos exercitar.
- Efetue as adições dos números, utilizando os dedos, outros objetos e mesmo a tabela apresentada acima.
- $\color{Blue}{9 + 12 = ?}$
- $\color{Blue}{15 + 8 = ?}$
- $\color{Blue}{16 + 9 = ?}$
- $\color{Blue}{21 + 5 = ?}$
- $\color{Blue}{33 + 4 = ?}$
- $\color{Blue}{27 + 3 = ?}$
- $\color{Blue}{35 + 8 = ?}$
- Efetue as adições dos números, escrevendo em colunas, como mostrado acima e efetue da direita para esquerda.
- $\color{Brown}{78 + 63 = ?}$
- $\color{Brown}{93 + 142 = ?}$
- $\color{Brown}{87 + 231 + 158 = ?}$
- $\color{Brown}{527 + 1872 = ?}$
- $\color{Brown}{2056 + 1932 = ?}$
- $\color{Brown}{5743 + 3278 + 7094 = ?}$
- Efetue as adições dos números, utilizando os dedos, outros objetos e mesmo a tabela apresentada acima.
Curitiba, 10 de julho de 2017 (Post refeito e ampliado nesta data).
Republicado em 25 de outubro de 2017.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com\decioadams.matfisonline
Celular e WhatsApp: (41) 9805-0732