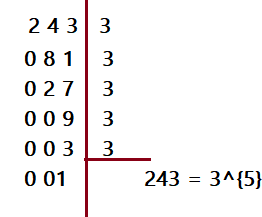Aprofundando radiciação
- Quando fazemos a decomposição do radicando em fatores primos e o exprimimos na forma de uma potência, teremos uma forma equivalente do radical. Por exemplo:
- $\color{Blue}{\root 3 \of{729} = \root 3 \of {3^6} }$
- Podemos colocar esse radical na forma de uma potência, onde o expoente é uma fração. O numerador é o expoente do radicando e o denominador é o índice do radical. Teremos então:
- $\color{Blue}{\root 3 \of {3^6} = 3^{\frac{6}{3}}}$
- Simplificando a fração, temos: ${3^2 = 9}$
- A raiz de índice n de um radicando na forma de potência pode ser sempre escrita na forma de uma potência com expoente fracionário e vice-versa. Se temos uma potência de expoente fracionário, podemos escrevê-la na forma de radical, cujo índice é o denominador do expoente e o numerador é o expoente da base.
- OBS.: quando o índice é 2, dizemos que a raiz é quadrada e quando o índice é 3, a raiz é cúbica. O índice 2 pode ser subentendido, uma vez que não faz sentido falar em raiz de índice 1(hum).
- Alguns exemplos.
- $\color{Blue}{\sqrt {7^5} = 7^{\frac{5}{2}}}$
- $\color{Blue}{\sqrt {256} = \sqrt {2^8} = 2^{\frac{8}{2}} = 2^4 = 16}$
- $\color{Blue}{\sqrt 5 = 5^{\frac{1}{2}}}$
- $\color{Blue}{\root 3 \of {2^6} = 2^{\frac{6}{3}} = 2^2 = 4}$
- $\color{Blue}{\root 4 \of{9^2} = 9^{\frac{2}{4}} = 9^{\frac{1}{2}} = \sqrt {9} = 3} $
- $\color{Blue}{\root 5 \of {2^{10}} = 2^{\frac{10}{5}} = 2^2 = 4}$
O exemplo 5 mostra que podemos dividir o índice e o expoente pelo mesmo número, de modo que o radical fique simplificado. Assim podemos fazer:
- $\color{Blue}{\root 6 \of {3^2} = \root 3 \of 3 = 3^{\frac{1}{3}}}$
- $\color{Blue}{\root 4 \of {5^6} = \sqrt {5^3} = 5^{\frac{3}{2}} = \sqrt{5^2\cdot 5} = 5\cdot\sqrt{5} } $
- Alguns exemplos para treinar. Vamos a eles.
- $\color{Brown}{\root 12 \of {64} = ?}$
- $\color{Brown}{\root 10 \of {25} = ?}$
- $\color{Brown}{\root 18 \of {256} = ?}$
- $\color{Brown}{\root 9 \of {125} = ?}$
- $\color{Brown}{\root 16 \of {128} = ?}$
- $\color{Brown}{\root 14 \of {144} = ?}$
- $\color{Brown}{\root 3 \of {512} = ?}$
- $\color{Brown}{\root 4 \of {49} = ?}$
- $\color{Brown}{\root 3 \of {32} = ?}$
Experimente criar alguns. Sugiro começar calculando as potências e depois fazer o processo contrário. Não importa que você saiba a resposta antecipadamente. O objetivo é exercitar. Ajuda a gravar os valores das potências mais comuns e suas raízes de diferentes índices. Não é nada desprezível conhecer alguns desses valores de memória. Ajuda muito em alguns momentos decisivos.
Essa memória me salvou uma questão numa prova no tempo de faculdade. Demorei a encontrar o caminho da resolução e quando faltavam apenas alguns segundos para o final do tempo, cheguei a raiz quadrada do número 1296. Para minha sorte, na noite anterior eu havia resolvido e determinado essa raiz com os meus alunos no ginásio, na 5ª série e não precisei calcular. Foi o tempo de escrever a resposta e entregar a prova. Nunca mais esqueci a resposta, que é 36.
Não é proibido decorar alguns, não que deva ser uma preocupação essencial, mas em muitos casos ajuda um bocado.
Até outro momento, com mais algumas coisas sobre o assunto.
Obs.: Em caso de dúvidas, não hesite em pedir ajuda. Para isso são os canais que informo logo abaixo. Também pode perguntar sobre outros assuntos que ainda não constem do blog. Esteja à vontade.
Curitiba, 09 de novembro de 2018
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732