Divisão.

• Vamos continuar aprendendo mais um pouco.
• Vou tentar apresentar alguns exemplos onde apareçam as dificuldades que podem atrapalhar e explicar como se procede para contornar.
• Vejamos o caso:
• $$\color{NavyBlue}{1516\div 76 = ?}$$

Temos que dividir os três primeiros algarismos do dividendo, para ser possível. Observe que ${15\div 7 = 2}$. Isso nos daria o primeiro algarismo do quociente igual a 2. Mas, ao multiplicar ${2\times 76 = 152}$, vemos que não é possível subtrair esse valor de ${151}$. Assim, temos que reduzir o primeiro algarismo do quociente para 1. Isso acontece com frequência. É preciso ter cuidado para não se perder nesse momento.

Colocando ${1}$ no quociente e fazendo a multiplicação, subtraímos de ${151-76 = 75}$. O resto é ${75}$. Note que faltou pouco para o quociente ser ${2}$. Baixamos o ${6}$ para a direita do resto e temos o número ${756}$. Importante notar que nunca se colocam dois algarismos de uma vez no quociente. Por isso o máximo que pode aparecer é ${9}$, nunca mais. A multiplicação ${9\times 76 = 684}$, subtraímos  ${756-684=72}$. Temos portanto o resultado da divisão: $\color{NavyBlue}{1516\div 76 = 19}$, $\color{NavyBlue}{resto = 72}$ $\Leftrightarrow $ $\color{NavyBlue}{19\times 76 + \color{Red}{72} = 1516}$

$\color{NavyBlue}{5356\div 52 = ?}$

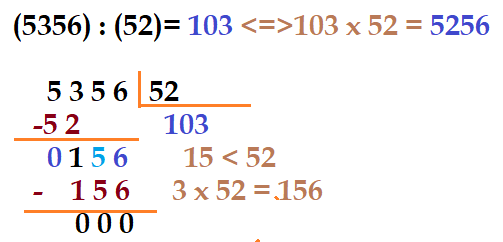
O primeiro algarismo do quociente será ${1}$ (um) e teremos resto ${1}$. Ao baixarmos o próximo algarismo, forma-se o número ${15\lt 52}$ e neste caso escrevemos, como próximo algarismo do quociente um ${0}$ (zero), antes de baixar o outro algarismo, formando agora o número ${156}$. A divisão de ${15\div5 = 3}$ o que deve permitir divisão por ${3}$ (três). Multiplicando ${3\times 52 = 156}$, que subtraído do dividendo, deixará resto${0}$ (zero). Resulta que $\color{NavyBlue}{5356\div 52 = 103}$, $\color{NavyBlue}{resto = 0}$ $\Leftrightarrow$ $\color{NavyBlue}{103\times 52 = 5356}$.

• $\color{NavyBlue}{4009\div 64 = ?}$

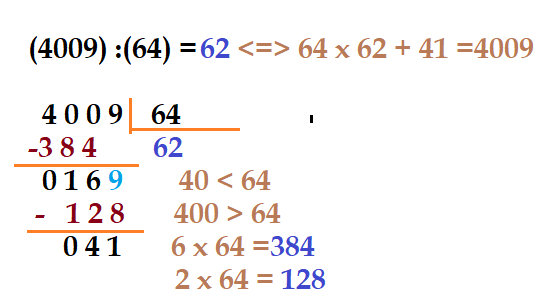
Os dois primeiros algarismos do dividendo formam um número menor que o divisor ${40\lt 64}$. Então temos que começar dividindo o número com três algarismos ${400\gt 64}$. Dividindo ${40\div 6 = 6}$, resto ${4}$. Devemos ter como primeiro algarismo do quociente o ${6}$ (seis). ${6\times 64 =384\lt 400}$. Subtraindo ${400 – 384 =16}$. Escrevemos ao lado direito do resto o último algarismo do dividendo, formamos ${169}$. A divisão ${16\div 6 = 2}$ com resto ${4}$. O próximo algarismo do quociente será ${2}$. ${2\times 64 = 128}$, que subtraído ${169 – 128 = 41}$. O quociente da divisão será pois ${62}$ e o resto ${41}$. Podemos escrever: $\color{NavyBlue}{4009\div 64 = 62}$, $\color{NavyBlue}{resto = 41}$, $\Leftrightarrow$ $\color{NavyBlue}{62\times 64 +\color{red}{41} = 4009}$

• $\color{navy}{2401\div 49 = ?}$

• O número para começar a divisão, deve ter três algarismos, pois ${24\lt 49}$. Então ${24\div 4 = 6}$. Fazendo ${6\times 49 = 294\gt 240}$ o que não permite a divisão. Diminuímos para ${5\times 49 = 245\gt 240}$, também não permite a divisão. Devemos começar com o algarismo ${4}$ no quociente. Multiplicando ${4\times 49 = 196}$. Subtraindo ${240 – 196 = 44}$.
• Escrevemos à direita do resto o último algarismo do dividendo ficamos com ${441}$. Dividindo ${44\div 4 = 11\gt 9}$. Portanto o próximo algarismo pode ser no máximo ${9}$. Multiplicamos ${9\times 49 = 441}$. Subtraímos ${441 – 441 = 0}$. Então:
• $\color{NavyBlue}{2401\div 49 = 49}$,$\color{NavyBlue}{resto = 0}$ $\Leftrightarrow$ $\color{NavyBlue}{49\times 49 = 2401}$.

• $\color{NavyBlue}{2581\div 89 =?}$

A divisão começa pelo número ${258}$, onde temos ${25\div 8 = 3}$, restando ${1}$. Multiplicando ${3\times 89 = 267\gt 258}$. Temos que diminuir uma unidade. Agora ${2\times 89 = 178}$, que diminuído ${258 – 178 = 80}$. Escrevendo o algarismo final ${1}$ à direita do resto fica ${801}$. Para saber o valor do próximo algarismo do quociente, vejamos quanto dá ${80\div 8 = 10\gt 9}$, por isso devemos usar no máximo ${9}$. Multiplicamos ${9\times 89 = 801}$. Diminuímos ${801 – 801 = 0}$. $\color{NavyBlue}{2581\div 89 = 29}$, $\color{NavyBlue}{resto = 0}$, $\Leftrightarrow$ $\color{NavyBlue}{29\times 89 = 2581}$.

Exercícios, lá vamos nós!

Efetue as divisões a seguir, usando para isso a forma de escrever os termos dentro da chave e realizando as operações, passo a passo. 

• $\color{OliveGreen}{3792\div 65 =?}$
• $\color{OliveGreen}{7921\div 89  = ?}$
• $\color{OliveGree}{4036\div 53  = ?}$
• $\color{OliveGreen}{5123\div 47 =?}$
• $\color{OliveGreen}{3584\div 37 = ?}$
• $\color{OliveGreen}{10548\div 96 =?}$
• $\color{OliveGreen}{3230\div 65 = ?}$
• $\color{OliveGreen}{3792\div 72 = ?}$
• $\color{OliveGreen}{9486\div 75 =?}$
• $\color{OliveGreen}{5392\div 82 =?}$

Obs.: Em caso de qualquer dúvida, faça contato com um dos meios abaixo para tirar suas dúvidas. Mande outro tipo de dúvida que tentarei ajudar se for possível. 

Confira as respostas que obteve para os exercícios acima. 

• $\color{OliveGreen}{3792\div 65 = 58 \Rightarrow (58\cdot 65) + 22}$
• $\color{OliveGreen}{7921\div 89 = 89\Rightarrow(89\cdot 89) = {(89)}^2}$
• $\color{OliveGreen}{4036\div 53  = 76\Rightarrow (76\cdot 53) + 8}$
• $\color{OliveGreen}{5123\div 47 =109\Rightarrow (109\cdot 47)}$
• $\color{OliveGreen}{3584\div 37 = 96 \Rightarrow(96\cdot 37) + 32}$
• $\color{OliveGreen}{10548\div 96 = 109 \Rightarrow (109\cdot 96) + 84}$
• $\color{OliveGreen}{3230\div 65 = 49 \Rightarrow (49\cdot 65) +45}$
• $\color{OliveGreen}{3792\div 72 = 52 \Rightarrow(52\cdot 72) + 48}$
• $\color{OliveGreen}{9486\div 75 =126 \Rightarrow(126\cdot 75) + 36}$
• $\color{OliveGreen}{5392\div 82 =65 \Rightarrow (65\cdot 82) + 62}$

Curitiba, 14 de julho de 2016. Revisado e atualizado em 12 de outubro de 2019.

Décio Adams

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular: (41) 99805-0732