Adição de frações.

• Frações com o mesmo denominador.

• Se os denominadores das frações são iguais, a adição será efetuada pela manutenção do denominador e adição dos numeradores.
• $\bbox[4px,border:2px solid Olive]{\mathbf{\color{Navy}{\frac{3}{7} + \frac{5}{7} + \frac{6}{7} = \frac{3 + 5 + 6}{7}}}}$

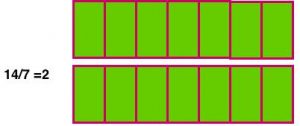
• Temos três retângulos, divididos em sete partes iguais. No primeiro tomamos $3$ (três) partes, no segundo $5$ (cinco) partes e no terceiro $6$ (seis) partes.
• Quantas partes iguais foram juntadas?
• É fácil constatar que foram $14$ partes. O que corresponde a exatamente dois inteiros.
• $\bbox[4px,border:2px solid Olive]{\mathbf{\color{Navy}{\frac {14}{7}  = 2}}}$

• No final foi possível fazer a divisão do numerador pelo denominador, resultando em um número inteiro. Vejamos outro exemplo.

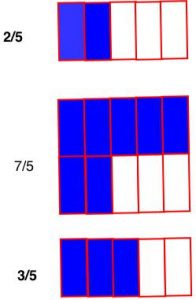
• Sejam as frações

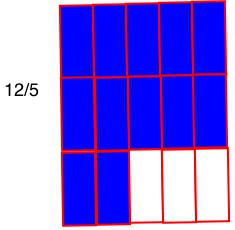
• $\bbox[4px,border:2px solid Olive]{\mathbf{\color{Navy}{\frac{2}{5} +\frac {7}{5} +\frac{3}{5} = \frac{2 + 7 + 3}{5}}}}$

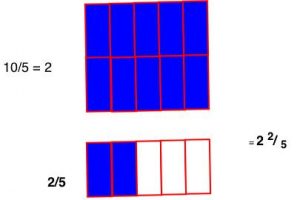
• $\bbox[4px,border:2px solid Olive]{\mathbf{\color{Navy}{\frac{12}{5} = 2\frac{2}{5}}}}$
• Nesse exemplo resultou da adição, uma fração imprópria. Podemos optar por deixar a resposta na forma de fração, ou transforma-la em número misto, extraindo os inteiros e escrevendo o número nessa nova forma.

• Para voltar à forma de fração imprópria, basta multiplicar o inteiro pelo denominador e adicionar o numerador, obtendo o numerador da fração imprópria.
• $\bbox[4px,border:2px solid Olive]{\mathbf{\color{Brown}{2\frac{2}{5} =\frac {{(2\cdot 5)} + 2}{5} = \frac{12}{5}}}}$

• Vamos exercitar essa operação.

  • $\mathbf{\color{Maroon}{\frac{7}{12} + \frac{6}{12} + \frac{5}{12} + \frac{3}{12}}}$
  • $\mathbf{\color{Maroon}{\frac{9}{11} +\frac{5}{11} +\frac{8}{11}}}$
  • $\mathbf{\color{Maroon}{\frac{8}{9} +\frac{5}{9} +\frac{2}{9}}}$
  • $\mathbf{\color{Maroon}{\frac{5}{8} + \frac{2}{8} + \frac{3}{8} + \frac{7}{8}}}$
  • $\mathbf{\color{Maroon}{\frac{7}{5} + \frac{2}{5} + \frac{4}{5}}}$
  • $\mathbf{\color{Maroon}{\frac{9}{7} + \frac{5}{7} + \frac{3}{7} + \frac{2}{7}}}$

• Frações com denominadores diferentes.

• Neste caso iremos recorrer novamente ao m.m.c. e reduzir as frações ao mesmo denominador, como fizemos na comparação de frações. Feito isso, bastará efetuar a adição dos numeradores e, se houver  possibilidade, simplificar o resultado. Pode ocorrer que resulte um inteiro ou uma fração imprópria que podemos transformar em número misto. Terá uma parte inteira e uma fração própria.

Veja o exemplo:

• $\mathbf{\color{Brown}{\frac{6}{5} + \frac{2}{7} +\frac{3}{10}}}$
• Os denominadores são 5, 7 e 10. Os dois primeiros são números primos. O último é múltiplo do primeiro (2 x 5= 10). De onde podemos inferir que o mmc dos denominadores é
• $\color{Navy}{2\times 5\times 7 = 70}$
• Ou fazemos a determinação, decompondo em fatores primos.
•  

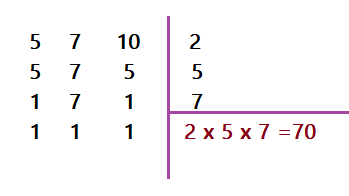
Vem então que:

• $\mathbf{\frac{6}{5} + \frac{2}{7} +\frac{3}{10}\\ = \frac{6\times {14} + 2\times {10} + 3\times7}{70} = \frac {84 + 20 + 21}{70}\\ = \frac{125}{70}  = \frac{25\times 5}{14\times 5}\\= \frac{25}{14} = 1\frac{11}{14}}$

• Mais um exemplo para entender melhor. Seja a adição das frações:
• $\mathbf{\color{Navy}{{3\over 5} + {4\over 3} + {2\over 7} + {3\over 2}}}$ 

Observando essas frações, vemos que seus denominadores são todos números primos. Nesse caso o mmc será igual ao produto de todos eles. Assim:

• $\color{Sepia}{m.m.c. (2,3,5,7)= {2\cdot 3\cdot 5\cdot 7}= 210}$

Assim sendo, a adição dessas frações fica assim.

• $\mathbf{\color{Navy}{\frac{3}{5} + \frac{4}{3} + \frac{2}{7} +\frac{3}{2} = \frac{{3\times 42} +{4\times 70} + {2\times 30} + {3\times 105}}{210} \\  = \frac{126 + 280 + 60 + 315}{210}  = \frac{781}{210} = 3\frac{151}{210}}}$

• Exercícios para sua diversão (kkkkkkk).

  • $\mathbf{\color{Brown}{\frac{3}{8} + \frac{1}{3} + \frac{2}{4} + \frac{3}{6}}}$
  • $\mathbf{\color{Brown}{\frac{5}{10} +\frac{2}{5} + \frac{3}{2}}}$
  • $\mathbf{\color{Brown}{\frac{7}{5} + \frac{5}{3} +\frac{2}{15} +\frac{4}{5}}}$
  • $\mathbf{\color{Brown}{\frac{8}{9} +\frac{6}{18} + \frac{5}{3}}}$

Obs.:Em caso de dúvidas, faça contato por um dos meios abaixo mostrados. Estou à disposição para ajudar e sanar suas dúvidas, orientar na superação das dificuldades.

Curitiba, 28 de março de 2015 (Reformulado em 21 de julho de 2016).

Republicado em 18 de novembro de 2017.

Décio Adams

[email protected]

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732