Divisão decimal aproximada.

Quando estudamos a divisão, vimos que grande parte das vezes essa operação não é exata, sobrando ao final do processo, um resto menor que o divisor. Naquele momento deixamos de efetuar esse complemento da operação. Ficamos com o resultado:

$\color{navy}{quociente\cdot divisor + resto = dividendo}$

Agora, vamos determinar o resultado da operação, com uma aproximação na forma de número decimal. Para isso recorremos à colocação de uma vírgula após o último algarismo inteiro obtido no quociente e acrescentamos um zero no resto. A partir daí tentamos continuar a divisão. Se ainda não for possível, acrescentamos um zero ao quociente e mais outro no resto. Podemos continuar assim indefinidamente. Talvez em algum momento ocorra uma divisão exata, ou então teremos uma dízima periódica, quando um ou mais algarismos começam a se repetir no quociente. O melhor de tudo é fazer isso na prática.

$\color{navy}{793\div 17 = ?}$
Colocamos os números na chave como há vimos antes e iniciamos o processo. Assim:

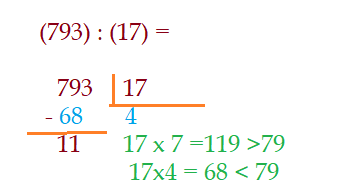
Primeiro passo da divisão. Vamos continuar, usando o outro algarismo do dividendo, acrescido ao resto que sobrou.

Começamos por dividir os dois primeiros algarismos, que formam o número ${79}$, pelo divisor ${17}$. Observando, notamos que não pode ser ${7}$ o quociente, pois a multiplicação entre ele e o divisor, ultrapassa em muito o dividendo ${79}$. É preciso baixar o valor. Iremos ver que a divisão é possível com ${4}$ no quociente, pois $\color{olive}{17\cdot 4 = 68\lt 79}$. Subtraindo ${68}$ de ${79}$, teremos no resto ${11}$. Colocamos ${4}$ no quociente, baixamos o último algarismo ${3}$ e voltamos a dividir.

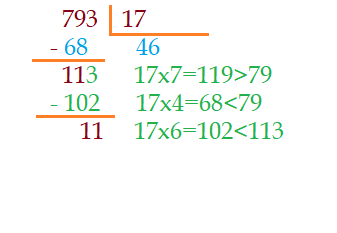
Para continuar, iremos colocar vírgula no quociente e acrescer um ${0}$ ao resto até aqui existente e assim seguiremos.

Temos agora $113$ dividido por ${17}$. Pelas multiplicações iremos verificar que podemos usar no máximo o número ${6}$. Fazendo $\color{olive}{17\cdot 6 = 102\lt113}$ e subtraímos esse valor do dividendo. Resta ${11}$.

Chegamos ao final com um resto ${1}$, sendo que o quociente já contém três algarismos após a vírgula.

Como não há mais algarismos no dividendo para baixar, colocamos a vírgula no quociente, após o algarismo ${6}$ e acrescentamos um ${0}$ após o resto ${11}$. Vamos agora dividir ${110}$ por ${17}$, o que novamente nos dá ${6}$. $\color{olive}{17\cdot 6 = 102\lt 110}$. Subtraindo do dividendo, nos resta agora ${8}$. Tornamos a acrescentar mais um $0$ ao resto e voltamos a dividir, agora ${80}$ por ${17}$, onde encontramos ${4}$. $\color{olive}{17\cdot 4 = 68\lt 80}$. Subtraimos de ${80}$ e temos resto ${12}$.

Com mais um ${0}$ acrescentado, temos agora ${120}$, dividido por ${17}$. O resultado é ${7}$ e $\color{olive}{17\cdot 7 = 119\lt 120}$. Subtraímos o produto do dividendo, restando agora apenas ${1}$. Se quisermos é possível continuar, mas na próxima tentativa de dividir, teremos ${1}0$ dividido por ${17}$, que não é possível. Colocaríamos um ${0}$ no quociente e acrescentaríamos outro no dividendo. Já temos no quociente três algarismos após a vírgula, o que corresponde a décimos, centésimos, milésimos. Não iremos encontrar o valor exato da divisão de qualquer maneira. Em diferentes situações poderemos precisar de mais ou menos algarismos decimais. Mas isso é assunto para outro momento. Podemos escrever $\color{navy}{(46,647)\cdot 17 \simeq 793}$

Divisão decimal exata

Vamos ver um outro exemplo. Seja $\color{navy}{67\div 4 = ?}$. Colocando na chave, teremos:

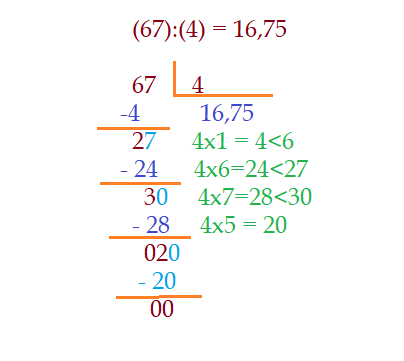
Começamos dividindo ${6}$ por ${4}$, obtendo ${1}$. Multiplicamos $\color{navy}{4\cdot 1 = 4\lt 6}$. Subtraimos e resta ${2}$. Baixamos o próximo algarismo, obtendo no dividendo ${27}$. Teremos no quociente o próximo algarismo ${6}$. $\color{navy}{6\cdot 4 = 24 \lt 27}$. Subtraimos e irá restar ${3}$.

Acrescentamos um ${0}$ e colocamos a vírgula no quociente. Temos agora ${30}$ dividido por ${4}$.

O próximo algarismo do quociente será ${7}$ e $\color{navy}{7\cdot 4 = 28\lt 30}$. Subtraindo do dividendo, resta ${2}$. Acrescentamos outro ${0}$ ao resto e teremos agora ${20}$ dividido por ${4}$. O algarismo no quociente será ${5}$. Multiplicamos $\color{navy}{5\cdot 4 = 20}$.

Subtraindo do dividendo, sobra agora resto ${0}$, indicando que a divisão, embora decimal, deu exata, pois não sobrou resto. Aqui podemos dizer que $\color{navy}{(16,75)\cdot 4 = 67}$

Outro exemplo de divisão decimal exata:

$\color{navy}{(3456)\div (25) = ?}$

A divisão de dois números inteiros, resultou num número decimal, sem sobrar resto, isto é, a divisão é exata.

Vamos a mais uns exemplos. $\color{brown}{12\div 45 = ?}$

A cada passo acrescentamos mais um zero no resto, enquanto os algarismos decimais vão se distanciando para direita da vírgula.

Observamos que o dividendo é menor que o divisor e portanto, não teremos nenhum algarismo na parte inteira. Nesse caso vamos colocar $0$ na parte inteira, seguido de vírgula e acrescentar $0$ à direita do dividendo. Assim passamos a dividir $120$ por $45$.

O máximo que podemos colocar no quociente é $2$. Multiplicando $\color{olive}{2\cdot (45) = 90\lt 120}$. Subtraimos e resulta resto $30$.

Acrescentamos um ${0}$ ao resto e dividimos agora ${300}$ por ${45}$. O resultado será ${6}$. Multiplicando teremos $\color{olive}{6\cdot (45) = 270\lt 300}$. Subtraindo, resta novamente ${30}$.

Acrescentamos novamente um ${0}$ e tornamos a dividir ${300}$ por ${45}$, resultando o mesmo no quociente e resto. Estamos diante de uma divisão que resulta em uma dízima periódica, isto é sempre irá sobrar resto ${30}$ e o algarismo ${6}$ irá se repetir no quociente sem parar. Neste caso temos uma dízima composta, pois o primeiro algarismo não faz parte do período, isto é, não se repete. $\color{brown}{(0,266…)\cdot (45) = 12}$.

Vejamos um exemplo de dízima simples, onde todos os algarismos se repetem na mesma ordem. $\color{olive}{10\div 7 = ?}$

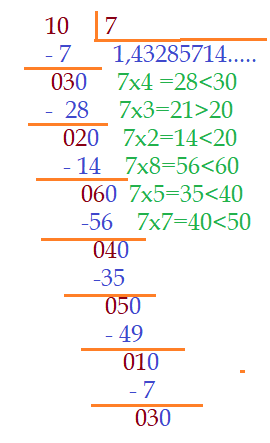
Dividindo ${10}$ por ${7}$, obtemos ${1}$ e o resto é ${3}$. Colocamos vírgula no quociente e acrescentamos um ${0}$.

Agora dividimos ${30}$ por ${7}$, obtendo no quociente o algarismo ${4}$. Multiplicando $\color{olive}{4\cdot 7 = 28\lt 30}$. Subtraindo, resta ${2}$. Acrescentamos um ${0}$ ao resto e continuamos.
A divisão de ${20}$ por ${7}$, nos dá no quociente o algarismo ${2}$ e o resto é ${6}$. Acrescentamos ao resto o algarismo ${0}$.
Agora temos ${60}$, dividido por ${7}$ e o algarismo do quociente será ${8}$. A multiplicação nos dá $\color{olive}{8\cdot 7 = 56\lt 60}$. Subtraindo temos ${4}$ ao qual acrescentamos um ${0}$.

O número ${40}$ dividido por ${7}$, nos dá no quociente o algarismo ${5}$. Multiplicando temos $\color{olive}{5\cdot 7 = 35\lt 40}$. O resto ao subtrair, será ${5}$ e acrescentamos a ele um ${0}$.

Ao acrescentar ${0}$ ao resto, obtivemos o número ${50}$. Na divisão, resulta o algarismo ${7}$ no quociente. Multiplicando e subtraindo, temos resto ${1}$. Acrescentando ${0}$, vamos para mais uma divisão.

O número ${1}$, acrescido de um ${0}$, dividido por ${7}$, nos fornece mais um algarismo ${1}$ no quociente e o resto volta a ser ${3}$. Notamos que começa aí a repetição dos algarismos. Embora na parte decimal, neste caso, o algarismo ${1}$ apareça no final, ele é o primeiro do período. Se estivéssemos dividindo $\color{olive}{1\div 7 =?}$, começaríamos por um ${0}$, seguido de vírgula. Todos os números que tenham por algarismo inicial ${1}$, seguido de um ou mais zeros, precedidos de um ou mais zeros, depois da vírgula, ao serem divididos por ${7}$, resultam na mesma sequência periódica de algarismos. O que muda é a posição da vírgula. Assim: $\color{navy}{(0,001)\div 7 = 0,000142857…}$ $\color{navy}{(0,01)\div 7 = 0,00142857…}$ $\color{navy}{(0,1)\div 7 = 0,0142857…}$ $\color{navy}{(1)\div 7 = 0,142857…}$ $\color{navy}{(10)\div 7 = 1,428571…}$ $\color{navy}{(100)\div 7 = 14,2857…}$ $\color{navy}{(1000)\div 7 = 142,857…}$

Essa situação é bastante comum e é útil em diversas ocasiões. Neste exemplo usei de propósito uma divisão que resultou em um período longo (seis algarismos). Há outros com períodos menores e estes são em maior número.

$\color{Brown}{(50)\div (30) = ?}$
$\color{Brown}{(132)\div (78) = ?}$
$\color{Brown}{(12)\div (19) = ?}$
$\color{Brown}{(5)\div (9) = ?}$
$\color{Brown}{(50)\div (30) = ?}$
$\color{Brown}{(150)\div (70) = ?}$
$\color{Brown}{(53)\div (75) = ?}$
$\color{Brown}{(250)\div (30) = ?}$
$\color{Brown}{(50)\div (22) = ?}$
$\color{Brown}{(525)\div (44) = ?}$
$\color{Brown}{(75)\div (30) = ?}$
$\color{Brown}{(648)\div (24) = ?}$
$\color{Brown}{(5)\div (45) = ?}$
$\color{Brown}{(3549)\div (328) = ?}$
$\color{Brown}{(143)\div (530) = ?}$
$\color{Brown}{(5960)\div (2580) = ?}$

Se tiver dúvidas sobre algum exercício ou de outros exercícios semelhantes encontrados em outras fontes, peça ajuda que não há problema. Estou à disposição.

Curitiba, 03 de outubro de 2019

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732