Função do primeiro grau.

1. Função linear

Quando exprimimos uma grandeza $\color{maroon}{y}$ em função de uma expressão do primeiro grau da grandeza $\color{maroon}{x}$, dizemos que temos uma $\color{blue}{funç\tilde{a}o}$ do primeiro grau. \[\bbox[5px,border:2px solid olive]{\color{navy}{y = f(x)}}\]

A função é denominada linear quando o termo independente é nulo ou inexistente. Quando a expressão do primeiro grau é completa ela ficará assim:

\[\bbox[5px,border:2px solid olive]{\color{navy}{y = b + a\cdot x}}\].

Essa função é denominada afim e será vista depois.

Assim:

\[\bbox[5px,border:2px solid olive]{\color{navy}{ y = a\cdot x}}\]

Domínio

É o conjunto numérico onde iremos encontrar os valores da variável $\color{maroon}{x}$.

Contra-domínio

É o conjunto numérico ao qual pertencem os valores da variável $\color{maroon}{y}$.

Na maior parte das vezes, consideramos tanto o domínio quanto o contra-domínio como sendo o o conjunto dos números reais. Para cada valor de $\color{maroon}{x}$ existe um valor correspondente de $\color{maroon}{y}$, formando um par ordenado, como vimos no produto cartesiano. Cada par ordenado identifica um ponto do plano cartesiano. Unindo esses pontos, teremos o gráfico da função. Vamos tomar por exemplo a função $\bbox[4px,border:2px solid olive]{\color{navy}{y = 2x}}$. Dizemos que $\bbox[4px,border:2px solid olive]{\color{navy}{y = f(x)}}$ definida no conjunto $\color{navy}{R}$. Vamos escolher alguns valores para a variável $\color{maroon}{x}$ e determinar os correspondentes valores de $\color{maroon}{y}$.

Para $x = 0$ $\Leftrightarrow $ $ y = 2\cdot 0 = 0$ e temos o par $\color{navy}{(0,0)}$

Para $x=-3$ $\Leftrightarrow$ $y = 2\cdot{(-3)} = -6$ e temos o par $\color{navy}{(-3, -6)}$

Para $x = -2$ $\Leftrightarrow$ $ y = 2\cdot{(-2)}= -4$ e temos o par $\color{navy}{(-2, -4)}$

Para $x = 2$ $\Leftrightarrow$ $y = 2\cdot 2 = 4$ e temos o par $\color{navy}{(2, 4)}$

Para $x = 3$ $\Leftrightarrow$ $y = 2\cdot 3 = 6$ e temos o par $\color{navy}{(3, 6)}$

É evidente que poderíamos determinar uma infinidade de outros pontos intercalados entre esses, mas veremos que o gráfico fica perfeitamente determinado com estes pontos. Vamos ver como fica esse gráfico?

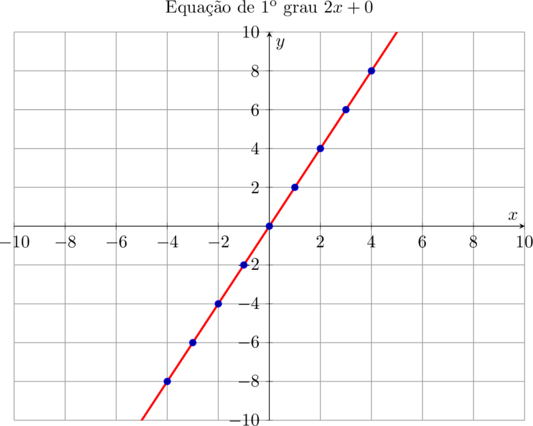
Podemos notar que o gráfico resultante é uma reta, que passa pelo ponto de coordenadas $\color{navy}{(0,0)}$. Vamos verificar o que acontece com a posição do gráfico, se tivermos o sinal do coeficiente $\color{maroon}{a}$ trocado, como em $\bbox[5px,border:2px solid olive]{\color{navy}{y = -2x + 0}}$.

Para $x = -3$ $\Leftrightarrow$ $y = -2\cdot {(-3)} = 6$ e temos o par $\color{navy}{(-3,6)}$

Para $x= -2$ $\Leftrightarrow$ $y=-2\cdot{(-2)} = 4$, temos o par $\color{navy}{(-2, 4)}$

Para $x=-1$ $\Leftrightarrow$ $y=-2\cdot{(-1)} = 2$, temos o par $\color{navy}{(-1,2)}$

Para$x =0$ $\Leftrightarrow$ $y =-2\cdot 0 =  0$, temos o par $\color{navy}{(0,0)}$

Para $x=1$ $\Leftrightarrow$ $y = -2\cdot 1 = -2$, temos o par $\color{navy}{(1,-2)}$

Para $x=2$ $\Leftrightarrow$ $y= -2\cdot 2 = -4$, temos o par $\color{navy}{(2,-4)}$

Para $x=3$ $\Leftrightarrow$ $y = -2\cdot 3 = -6$, temos o par $\color{navy}{(3,-6)}$

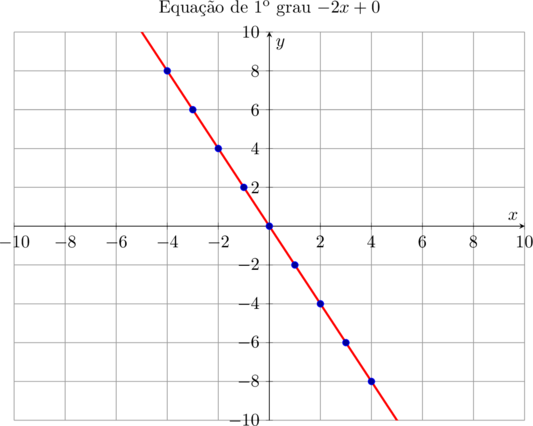
Observamos que a inclinação mudou de lado, isto é, o ângulo entre a reta do gráfico e o semi-eixo positivo de $x$ fica aumentado. Assim fica fácil entender que o valor e o sinal do coeficiente $\color{navy}{a}$ determina a posição e o ângulo. Daí ser este coeficiente chamado de coeficiente angular e é determinado pelo valor de \[\color{blue}{a = \frac{\Delta y}{\Delta x}}\]

Este número, denominado coeficiente angular, representa na verdade a razão trigonométrica $\color{navy}{\tan\theta}$, do ângulo formado entre o semi-eixo $\color{navy}{x}$ e a reta gráfica. Para observar esse fato, vamos pegar várias funções lineares, com diferentes coeficientes $\color{navy}{a}$, e representar no mesmo plano cartesiano, observando a variação da posição da reta, em consequência da variação do coeficiente.

Seja $\color{blue}{y = \frac{x}{2}}$; $\color{blue}{y = 3x}$; $\color{blue}{y = – 3x}$ e $\color{blue}{y = -\frac{x}{2}}$. Vamos determinar alguns pares ordenados para as funções e depois representar no plano cartesiano.

Em $\color{blue}{y = \frac{x}{2}}$, teremos:

• para $x=8$ $\Leftrightarrow$ $ y=\frac{8}{2} = 4$, formando o par $\color{navy}{(8,4)}$
• para $x = 4$ $\Leftrightarrow$ $y = \frac{4}{2} = 2$, formando o par $\color{navy}{(4,2)}$
• para $x =0$ $\Leftrightarrow$ $ y = \frac{0}{2} = 0$, formando o par $\color{navy}{(0,0)}$
• para $x =-4$ $\Leftrightarrow$ $y = \frac{-4}{2} =-2$, formando o par $\color{navy}{(-4,-2)}$
• para $x=-8$ $\Leftrightarrow$ $y= \frac{-8}{2} = -4$, formando o par $\color{navy}{(-8,-4)}$

Em $\color{blue}{y = 3x}$, teremos:

• para $x=3$ $\Leftrightarrow$ $y= 3\cdot{3} = 9$, formando o par $\color{navy}{(3,9)}$
• para $x=2$  $\Leftrightarrow$ $y=3\cdot 2 = 6$, formando o par $\color{navy}{(2,6)}$
• para $x=1$  $\Leftrightarrow$ $y=3\cdot 1= 3$, formando o par $\color{navy}{(1,3)}$
• para $x=0$ $\Leftrightarrow$ $y =0\cdot 0 = 0$, formando o par $\color{navy}{(0,0)}$
• para $x=-1$ $\Leftrightarrow$ $y =3\cdot{(-1)}=-3$,formando o par $\color{navy}{(-1,-3)}$
• para $x=-2$  $\Leftrightarrow$ $y=3\cdot{(-2)}=-6$, formando o par$\color{navy}{(-2,-6)}$
• para $x =-3$ $\Leftrightarrow$ $y=3\cdot(-3)=-9$, formando o par $\color{navy}{(-3,-9)}$

Em $\color{blue}{y = – 3x}$ teremos:

• para $x=3$ $\Leftrightarrow$ $y =-3\cdot 9= -9$, formando o par $\color{navy}{(3,-9)}$
• para $x=2$ $\Leftrightarrow$ $y=-3\cdot 2= -6$, formando o par $\color{navy}{(2,-6)}$
• para $x=1$ $\Leftrightarrow$ $y=-3\cdot 1=-3$, formando o par $\color{navy}{(1,-3)}$
• para $x=0$ $\Leftrightarrow$ $y = -3\cdot 0 = 0$, formando o par $\color{navy}{(0,0)}$
• para $x=-1$ $\Leftrightarrow$ $y=-3\cdot{(-1)}=3$, formando o par $\color{navy}{(-1,3)}$
• para $x=-2$ $\Leftrightarrow$ $y=-3\cdot{(-2)}=6$, formando o par $\color{navy}{(-2,6)}$
• para $x=-3$ $\Leftrightarrow$ $y=-3\cdot{-3} = 9$,formando o par $\color{navy}{(-3,9)}$

Em $\color{blue}{y = -\frac{x}{2}}$, teremos:

• para $x=8$  $\Leftrightarrow$ $y=-\frac{(8}{2} =-4$, formando o par $\color{navy}{(8,-4)}$
• para $x=4$ $\Leftrightarrow$ $y =-\frac{4}{2} = -2$, formando o par $\color{navy}{(4,-2)}$
• para $x=0$ $\Leftrightarrow$ $y =-\frac{0}{2} = 0$, formando o par $\color{navy}{(0,0)}$
• para $x=-4$ $\Leftrightarrow$ $y =-\frac{-4}{2} = 2$, fornando o par $\color{navy}{(-4,2)}$
• para $x=-8$ $\Leftrightarrow$ $y= -\frac{-8}{2} = 4$, formando o par $\color{navy}{(-8,4)}$

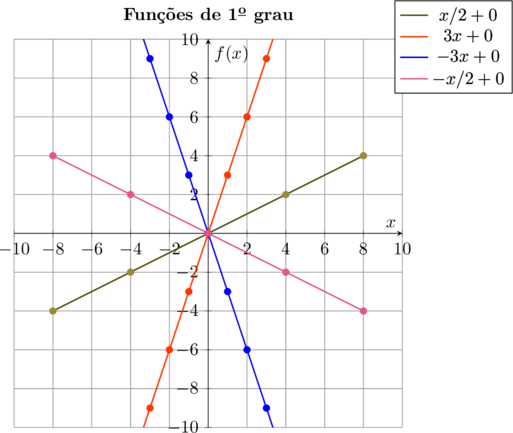
Observando as posições das retas, percebemos que elas todas passam pela origem do plano cartesiano, isto é têm em comum um ponto que é o de coordenadas $\color{navy}{(0,0)}$. duas abrangem o primeiro e terceiro quadrante e duas o segundo e quarto quadrante. Vamos determinar os coeficientes angulares de cada uma delas.

Para a primeira temos: $\color{navy}{ a_1 = \frac{2}{4} = \frac{1}{2}}$

Para a segunda, temos: $\color{navy}{ a_2 = \frac{9}{3} = 3} $

Para a terceira, temos: $\color{navy}{a_3 = \frac{-9}{3} = -3} $

Para a quarta, temos: $\color{navy}{a_4= \frac{4}{-8} =-\frac{1}{2}} $

Fica fácil de observar que, estando a função na sua forma mais simples, o coeficiente angular da reta, corresponde ao coeficiente do termo que contém a variável $\color{maroon}{x}$.

Para fixar o assunto, vejamos alguns exemplos para cada um exercitar no tempo que tiver disponível.

1. Determine alguns pares ordenados para cada uma das funções lineares e construa o gráfico correspondente, em papel milimetrado, ou na falta deste, usando uma régua e uma folha de papel que tenha.

a) $\color{blue}{ y = 4x}$                                           b)$\color{blue}{y =\frac{1}{3}\cdot x}$

c) $\color{blue}{y = -5x }$                                         d)$\color{blue}{y = \frac{2}{3}\cdot x}$

e)$\color{blue}{y =-\frac{3}{5}\cdot x}$                  f)$\color{blue}{y = -\frac{5x}{4}}$

As dúvidas que restarem podem ser sanadas usando um dos canais abaixo listados. Mesmo exemplos de outras origem podem ser apresentados para consultas. Estou à disposição de quem necessitar.

Curitiba, 28 de junho de 2016. Revisado e republicado em 08/10/2019

Décio Adams

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular: (41) 99805-0732