Função afim!
Achou engraçado?
Mas é esse mesmo o nome que damos a uma função do primeiro grau, cuja representação gráfica cartesiana, não passa pela origem do sistema de eixos cartesianos. Sua forma geral é do tipo \[\bbox[5px,border:2px solid olive]{\color{maroon}{ y = a\cdot x + b }}\]
Coeficiente angular
O coeficiente do termo $\color{navy}{ax}$ é também nesse caso o coeficiente angular, indicando a inclinação da reta gráfica, em relação ao eixo das abcissas.
Coeficiente linear
Vejamos o que acontece se substituirmos a variável $\color{navy}{x}$ pelo valor 0(zero).
$ y = a\cdot 0 + b $ $\Leftrightarrow$ $ y = 0 + b = b $ $\Leftrightarrow$ $ y = b $
Isto significa que o ponto do plano cartesiano, corresponde ao valor do termo independente $\color{navy}{b}$, tem como abcissa o número $\color{navy}{0}$. Neste ponto ocorre a intersecção do gráfico, com o eixo das ordenadas.
Nada melhor do que verificar como é que isso fica na prática. Seja a função $\color{navy}{y =f(x)}$, definida por $\color{navy}{y= x + 3}$.
- Para $x=-10$ $\Leftrightarrow$ $y=-10 + 3=-7$, formando o par $\color{blue}{(-10,-7)}$.
- Para $x= -7$ $\Leftrightarrow$ $y =-7 + 3 =-4$, formando o par $\color{blue}{(-7,-4)}$.
- Para $x= -5$ $\Leftrightarrow$ $y=-5 + 3 =-1$, formando o par $\color{blue}{(-5,-2)}$.
- Para $x=-3 $ $\Leftrightarrow$ $y=-3 +3 = 0$, formando o par $\color{maroon}{(-3,0)}$.
- Para $x= 0$ $\Leftrightarrow$ $y =0 + 3 = 3$, formando o par $\color{maroon}{(0,3)}$.
- Para $x= 3$ $\Leftrightarrow$ $y = 3 + 3= 6$, formando o par $\color{blue}{(3,6)}$.
- Para $x=5$ $\Leftrightarrow$ $y = 5+ 3 =8$, formando o par $\color{blue}{(5,8)}$.
- Para $x=7$ $\Leftrightarrow$ $y= 7 + 3 =10$, formando o par $\color{blue}{(7,10)}$.
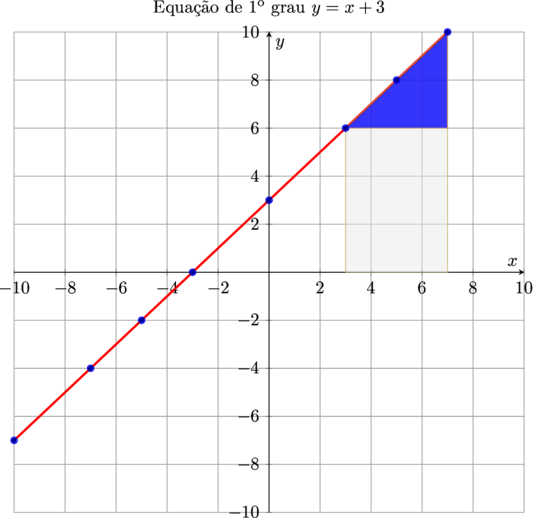
Podemos observar que o ponto em que o gráfico intercepta o eixo $\color{blue}{x}$, é o ponto indicado pelo número $\color{blue}{3}$, ou seja o coeficiente linear é $\color{olive}{b = 3}$.
O coeficiente angular pode ser determinado pelos valores das coordenadas de dois pontos. Podemos usar pontos de nossa livre escolha, como por exemplo $\color{blue}{(7,10) (3,6)}$, vértices dos ângulos agudos do triângulo destacado no gráfico.
\[\Delta y = 10 – 6 = 4\]
\[\Delta x = 7 – 3 = 4\]
\[ a =\frac{\Delta y}{\Delta x}\]
\[a = \frac{4}{4} = 1\]
\[ a = 1\]
Só para ver, vamos usar a mesma função, trocando o sinal do coeficiente linear. Teremos então: $\color{navy}{y = f(x)}$ , definida por $\color{navy}{y = x – 3}$
Vamos apenas determinar os pontos para traçar a reta.
- para $x =-7$ $\Leftrightarrow$ $y=-7 – 3 = -10$, formando o par $\color{navy}{(-7,-10)}$.
- para $x= -4$ $\Leftrightarrow$ $y=-4 – 3 =-7 $, formando o par $\color{navy}{(-4,-7)}$.
- para $ x= o$ $\Leftrightarrow$ $y= 0 – 3 = -3$, formando o par $\color{navy}{(0,-3)}$.
- para $x = 3$ $\Leftrightarrow$ $y = 3 – 3= 0$, formando o par $\color{navy}{(3,0)}$.
- para $x= 7$ $\Leftrightarrow$ $y = 7 – 3 = 4$, formando o par $\color{navy}{(7,4)}$.
- para $x= 10$ $\Leftrightarrow$ $y=10 -3= 7$,formando o par $\color{navy}{(10,7)}$.
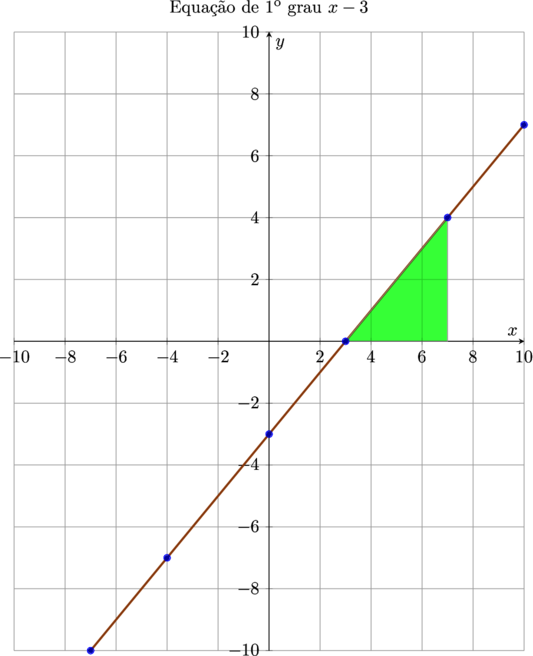
A nova função, tem o mesmo coeficiente angular $\color{blue}{a = 1}$. Os vértices dos ângulos agudos destacados no gráfico, permitem determinar o valor do coeficiente angular.
\[a = \frac{4 – 0}{7-3} =\frac{4}{4} = 1\]
O coeficiente linear $\color{blue}{b= -3}$. Se as retas tem a mesma inclinação em relação aos eixos cartesianos, e estão separadas de uma distância constante, elas são retas paralelas. Assim como elas poderíamos traçar uma infinidade de outras, paralelas a elas e deslocadas para cima ou para baixo no plano cartesiano.
- Vamos representar no mesmo plano cartesiano as funções afim a seguir.
a)${y = 2x – 1}$
b)${y = 2x +1}$
c)${y = 2x + 2}$
d)${y = 2x -2}$
2. Identifique os coeficiente escreva a função afim correspondente aos gráficos abaixo.
a)
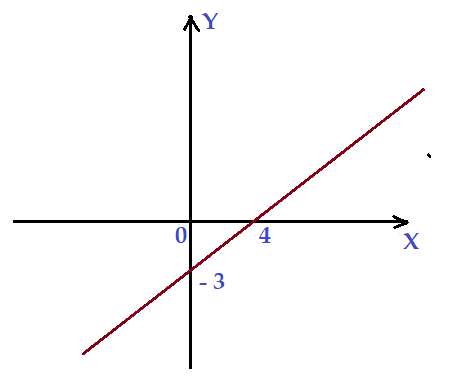
b)
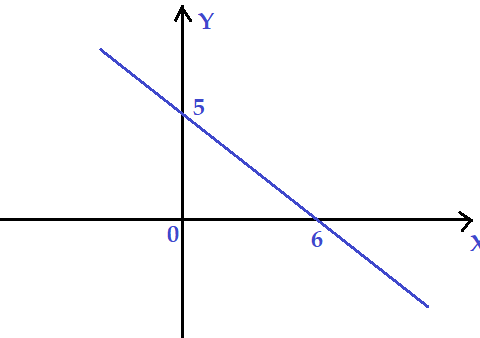
c)
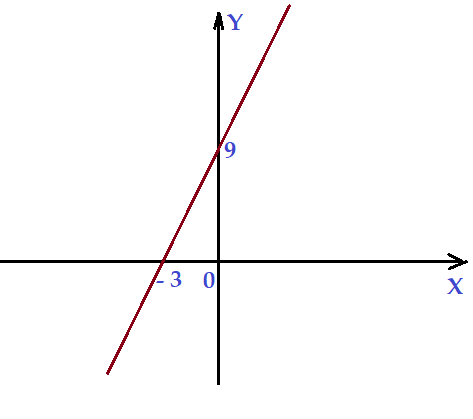
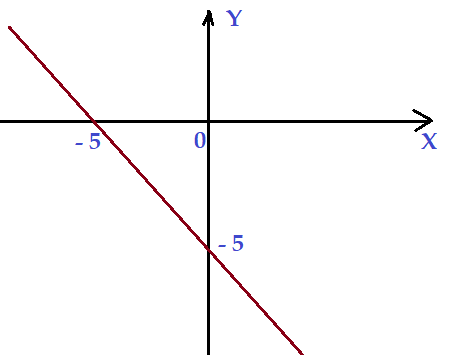
d)
Curitiba, 29 de junho de 2016. Revisto e melhorado no dia 08 de outubro de 2019.
Obs.: Em caso de dúvidas, pergunte por intermédio de um dos canais abaixo listados. Nem se sinta constrangido de pedir ajuda na solução de exercícios vindos de outra origem. Estou aqui para ajudar sempre. Disponha.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular: (41) 99805-0732

