Vamos subtrair
Começaremos por dizer que a subtração é a operação inversa da adição. Se na adição nós juntamos, reunimos os elementos de mais de um conjunto, na subtração fazemos o contrário. Retiramos, diminuimos os elementos de um conjunto(subtraendo), dos elementos de outro conjunto(minuendo) normalmente maior. Por exemplo:
- ${(♠, ♠, ♠, ♠, ♠, ♠, ♠)} – {(♠, ♠, ♠)} $
- $= {(♠, ♠, ♠, ♠,\underbrace{ ♠, ♠, ♠})} ={(♠, ♠, ♠, ♠)}$
- 7 – 3 = 4
Na forma de conjuntos, basta contar os elementos a serem subtraídos(subtraendo), retirando-os do conjunto (minuendo) e teremos um conjunto que é igual a diferença entre os dois. No exemplo temos 7 elementos no minuendo e 3 no subtraendo. Restaram 4 elementos no conjunto diferença. Para conferir se está certo, basta contar os elementos do resto, junto com os elementos do subtraendo e deveremos encontrar o minuendo. Você pode usar os dedos das suas mãos, dos pés, outros objetos para formar os conjuntos que ajudarão a efetuar essas operações. Com isso logo, logo, saberá de cor e salteado a diferença entre esses números pequenos, ficando mais fácil obter o resultado.
Quando tivermos que subtrair números com vários algarismos, novamente recorremos às colunas, escrevendo os números em conforme as ordens e classes que os algarismos ocupam nesses números. Vamos a um exemplo.
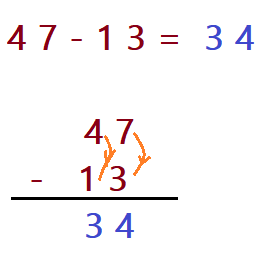
- $$\color{Sepia}{47 – 13 =?}$$
Na coluna das unidades vamos fazer (7 – 3 = 4) e na coluna das dezenas (4 – 1 = 3). O que nos dá a diferença igual a 34 (resto).
$$\color{NavyBlue}{47 – 13 = 34}$$
- $$\color{Sepia}{569 – 235 =?}$$
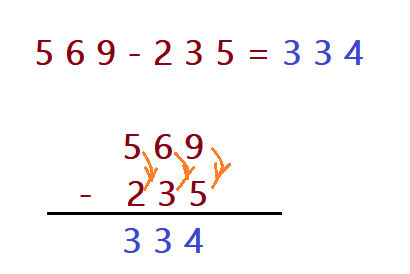
As unidades nos apresentam (9 – 5 = 4), nas dezenas (6 – 3 = 3) e nos milhares (5 – 2 = 3). Escrevendo esses algarismos nas colunas corretas, resulta a diferença entre os dois números igual a 334.
$$\color{NavyBlue}{569 – 235 = 334}$$
Antes do próximo passo, alguns exercícios para sedimentar a aprendizagem.
- Efetue as subtrações
- $65 – 43 =?$
- $76 – 35 =?$
- $254 – 132 =?$
- $529 – 314 =?$
- $3576 – 2354 =?$
- $8357 – 5236 = ?$
Observe que nos exemplos e exercícios acima, propositalmente eu coloquei números de modo que sempre o algarismo do minuendo é maior que o subtraendo. O objetivo era mostrar como se procede nesse caso.
Agora, vamos ver o que fazer quando se trata de subtrair um algarismo maior de um menor. Olha só:
- $$\color{Sepia}{46 – 29 =?}$$
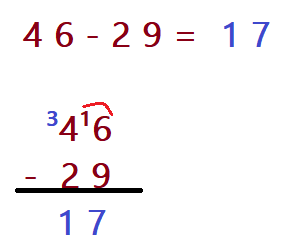
Observe que na coluna das dezenas temos (6 – 9 = ?). Com o que aprendemos até aqui, não é possível subtrair 9 unidades de onde há somente 6 delas. O que as pessoas, principalmente nas comunidades menores, onde todos se conhecem, fazem se por acaso faltar açúcar para adoçar o café ou o chá? Alguém corre até a vizinha e pede uma xícara ou copo do produto emprestado. Quando comprar, devolve e pronto. Nós vamos fazer algo parecido. Veja o algarismo das dezenas. Ele tem unidades sobrando em relação ao subtraendo e pode emprestar uma dezena ao 6, formando então 16, o que torna possível a subtração ( 16 – 9 = 7).
Como o 4 emprestou uma dezenas de unidades ao seu “vizinho” 6, ele agora só possui mais 3 dezenas e a operação fica assim (3 – 2 = 1). Colocamos os dois algarismos nas colunas e formamos o número 17, que é a diferença dos números dados.
$$\color{NavyBlue}{46 – 29 = 17}$$
- $$\color{Sepia}{607 – 259 =?}$$
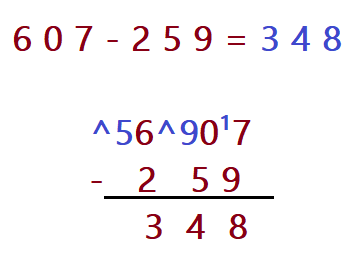
Note que nas unidades temos (7 – 9 = ?). Não é possível. Precisamos emprestar do vizinho. Mas a casa vizinha está vazia, não mora ninguém (0). Vamos emprestar uma unidade de centenas ao 6, nessa ordem. Uma centena tem dez dezenas e o (0) também vai precisar emprestar para poder subtrair dele o 5. Então pegamos uma das 10 dezenas e juntamos ao 7, formando 17 e as outras 9 dezenas ficam no lugar do (0) e podemos fazer a subtração (17 – 9=8). Depois (9 – 5 = 4) e por último (5 – 2 = 3). Não podemos esquecer que o 6 emprestou uma de suas centenas aos vizinhos “mais pobres” para que eles pudessem pagar a “conta” (kkkkkkk).
Colocamos os resultados nas suas colunas e temos
$$\color{NavyBlue}{607 – 259 = 348}$$
- $$\color{Sepia}{3479 – 1684 =?}$$
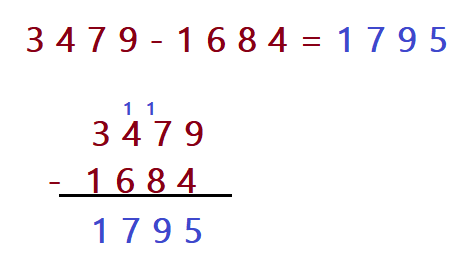
Na coluna das unidades temos (9 – 4 = 5). Na coluna das dezenas (7 – 8=?) o que é impossível. Vamos ver se o vizinho empresta uma centena. O vizinho tem 4 unidades de centena e pode emprestar uma. Fica (17 – 8 = 9). Agora nas centenas ficou (3 – 6 =?) é impossível. Novamente emprestamos do vizinho, mais rico, que tem 3 milhares e pode emprestar. Ficamos com (13 – 6 = 7) e por último nos milhares ficamos com (2 – 1 = 1). Temos todos os algarismos para formar o número que é a diferença.
$$\color{NavyBlue}{3479 – 1684 =1795}$$
Vamos ver se ficou entendido. Se ficar alguma dúvida, pergunte que eu esclareço depois. Chegou a vez de fazer exercícios.
- Efetue as subtrações.
- $73 – 32 =?$
- $92 – 57 =?$
- $167 – 86 =?$
- $462 – 349 =?$
- $853 – 537 =?$
- $651 – 423 =?$
- $1567 – 925 =?$
- $3749 – 1567 =?$
- $20534 – 12528 =?$
- $5781 – 4059 =?$
- $6724 – 2549 =?$
- $17243 – 8934 = ?$
Prova real
Dissemos no começo do texto que a subtração é a operação inversa da adição. Se isso é verdadeiro, deve ser possível tirar a prova, isto é, verificar se o resultado está correto. Vamos ver como é que se faz isso?
Se: $\color{Sepia}{607 – 259 = 348}$, então
$$\color{NavyBlue}{348 + 259 = 607}$$

Se fizermos a soma do resto (diferença) com o subtraendo, encontraremos o minuendo. Isso sempre será verdadeiro e vale a mesma coisa, apenas em sentido inverso para tirar a prova da soma.
Curitiba, 02 de outubro de 2017
Atualizado em 16 de junho de 2018
Decio Adams, IWA
www.facebook.com/livros.decioadams
Telefone: (41) 3019-4760
Celular WhatsApp: (41) 99805-0732

