Funções com gráficos paralelos.

Como vimos nos dois posts anteriores, existem funções de primeiro grau, cujos gráficos são paralelos. Basta que elas tenham coneficientes angulares iguais. O que as diferencia, é o coeficiente linear, ou seja, o número que não está ligado a uma variável pela operação de multiplicação ou divisão.

Lembrando: $\bbox[5px,border:2px solid olive]{\color{navy}{ y = ax + b}}$

O coeficiente angular é o número que ocupa o lugar da letra $\color{navy}{a}$ e o coeficiente linear é o número que ocupa o lugar da letra $\color{navy}{b}$

Vejamos um grupo de funções, cujos gráficos são retas ascendentes, paralelas. \[\color{maroon}{ y = 3x – 9}\] \[\color{maroon}{ y = 3x – 6}\] \[\color{maroon}{ y = 3x – 3}\] \[\color{maroon}{ y = 3x + 3}\] \[\color{maroon}{ y = 3x + 6}\] \[\color{maroon}{ y = 3x + 9}\] \[\color{maroon}{ y = 3x + 0}\]

A geometria e o desenho geométrico nos ensinam que para traçar uma reta, basta conhecer dois de seus pontos. Por isso, para facilitar, vamos determinar os pares ordenados que identificam os dois pontos em que as retas gráficas das funções acima, interceptam os eixos cartesianos.

\[\bbox[4px,border:2px solid olive]{\color{maroon}{ y = 3x – 9}}\]

para $x = 0 $ $\Rightarrow$ $ y = 3\cdot{0} – 9 = – 9 $ $ \rightarrow $ $ (0,-9) $
para $x =3 $ $\Rightarrow$ $ y = 3\cdot{3} – 9=0$ $\rightarrow$ $ (-3, 0)$

\[\bbox[4px,border:2px solid olive]{\color{maroon}{ y = 3x – 6}}\]

para $x = 0$ $\Rightarrow$ $y = 3\cdot 0 – 6 = -6$ $\rightarrow$ $ (0,-6) $
para $x = 2 $ $\Rightarrow$ $y =3\cdot 2 -6 = 0$ $\rightarrow$ $(2,0)$

\[\bbox[4px,border:2px solid olive]{\color{maroon}{ y = 3x – 3}}\]

para $x = 1$ $\Rightarrow$ $y =3\cdot{1} -3 = 0$ $\rightarrow$ $(1,0)$
para $x=0$ $\Rightarrow$ $y= 3\cdot 0 -3 = – 3$ $\rightarrow$ $(0,-3)$

\[\bbox[4px,border:2px solid olive]{\color{maroon}{ y = 3x + 3}}\]

para $x =0$ $\Rightarrow$ $ y = 3\cdot 0 + 3 = 3$ $\rightarrow$ $(0,3)$
para $x = – 1$ $\Rightarrow$ $y =3\cdot{-1} + 3 = 0$ $\rightarrow$ $(-1,0)$

\[\bbox[4px,border:2px solid olive]{\color{maroon}{ y = 3x + 6}}\]

para $x = 0$ $\Rightarrow$ $y = 3\cdot 0 + 6 = 6$ $\rightarrow$ $(0,6)$
para $x = -2$ $\Rightarrow$ $y =3\cdot{(-2)} +6 = 0 $ $\rightarrow$ $(-2,0)$

\[\bbox[4px,border:2px solid olive]{\color{maroon}{ y = 3x + 9}}\]

para $x = 0$ $\Rightarrow$ $y = 3\cdot 0 + 9 = 9$ $\rightarrow$ $(0,9)$
para $x= -3$ $\Rightarrow$ $y =3\cdot{-3} + 9 = 0$ $\rightarrow$ $(-3, 0)$

\[\bbox[4px,border:2px solid olive]{\color{maroon}{ y = 3x + 0}}\]

para $x = 0$ $\Rightarrow$ $y = 3\cdot 0 = 0 $ $\rightarrow$ $(0,0)$
para $x = 3 $ $\Rightarrow$ $y = 3\cdot 3 = 9$ $\rightarrow$ $(3,9)$
para $x = -3$ $\Rightarrow$ $ y = 3\cdot{(-3)} = -9$ $\rightarrow$ $(-3,-9)$

Rendered by QuickLaTeX.com

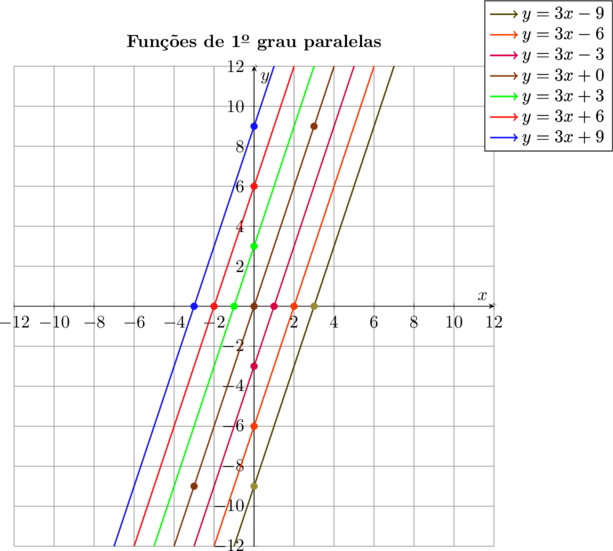
Podemos notar que todas as retas são ascendentes, e paralelas. Os coeficientes lineares começam com $\color{maron}{-9}$ e terminam em $\color{maroon}{9}$. pelas equações, vemos que em todas aparece o coeficiente $\color{navy}{a = 3}$ e portanto todas têm o mesmo coeficiente angular.

Eu coloquei propositalmente entre elas uma função linear, com o mesmo coeficiente angular e podemos observar que ela também é paralela as demais. O que nos mostra que a função denominada linear, é na verdade um caso particular das outras, pois ela tem a característica de passar na origem dos eixos cartesianos, no ponto $\color{navy}{(0,0)}. Assim sendo, pode-se traçar num mesmo plano cartesiano, infinitas retas paralelas, com a mesma inclinação, diferindo entre si apenas pelo valor do coeficiente linear, isto é, o ponto em que elas interceptam o eixo das ordenadas.

Vamos ver agora um exemplo semelhante, com o coeficiente angular negativo. Sejam as funções \[\bbox[4px,border:2px solid olive]{\color{maroon}{y=-2x – 10}}\]

para$x=-5$ $\Rightarrow$ $y = -2\cdot{-5} – 10 = 0$ $\rightarrow$ $\color{navy}{(-5,0)}$;
para$x= 0$ $\Rightarrow$ $y = -2\cdot 0 -10 = -10$ $\rightarrow$ $\color{navy}{(0,-10)}$;

\[\bbox[4px,border:2px solid olive]{\color{maroon}{y = -2x – 6}}\]

para$x= 0$ $\Rightarrow$ $y = -2\cdot 0 -6 = – 6$ $\rightarrow$ $\color{navy}{(0,-6)}$;
para$x= -3$ $\Rightarrow$ $y = -2\cdot {-3} -6 = 0 $ $\rightarrow$ $\color{navy}{(-3,0)}$;

\[\bbox[4px,border:2px solid olive]{\color{maroon}{y = -2x -2}}\]

para$x= 0$ $\Rightarrow$ $y = -2\cdot {0} -6 = -2 $$\rightarrow$ $\color{navy}{(-1,0)}$;

\[\bbox[4px,border:2px solid olive]{\color{maroon}{y = -2x + 0}}\]

para$x= -5$ $\Rightarrow$ $y = -2\cdot {-5} = 10 $ $\rightarrow$ $\color{navy}{(-5,10)}$;
para$x= 0$ $\Rightarrow$ $y = -2\cdot {0} = 0 $ $\rightarrow$ $\color{navy}{(0,0)}$;
para$x= 5$ $\Rightarrow$ $y = -2\cdot {5} = -10 $ $\rightarrow$ $\color{navy}{(5,-10)}$;

\[\bbox[4px,border:2px solid olive]{\color{maroon}{y = -2x +2}}\]

para$x= -0$ $\Rightarrow$ $y = -2\cdot {0} +2 = -2 $ $\rightarrow$ $\color{navy}{(0,-2)}$;
para$x= 1$ $\Rightarrow$ $y = -2\cdot {1} +2 = 0 $ $\rightarrow$ $\color{navy}{(1,0)};$

\[\bbox[4px,border:2px solid olive]{\color{maroon}{y = -2x +6}}\]

para$x= 0$ $\Rightarrow$ $y = -2\cdot {0} + 6 = 6 $ $\rightarrow$ $\color{navy}{(0,6)}$;
para$x= 3$ $\Rightarrow$ $y = -2\cdot {3} + 6 = 0 $ $\rightarrow$ $\color{navy}{(3,0)}$;

\[\bbox[4px,border:2px solid olive]{\color{maroon}{y = -2x + 10}}\]

para$x= 0$ $\Rightarrow$ $y = -2\cdot {0} +10 = -10 $ $\rightarrow$ $\color{navy}{(0,10)}$;
para$x= 5$ $\Rightarrow$ $y = -2\cdot {5} +10 = 0 $ $\rightarrow$ $\color{navy}{(5,0)}$;

Representando graficamente, teremos:

Rendered by QuickLaTeX.com

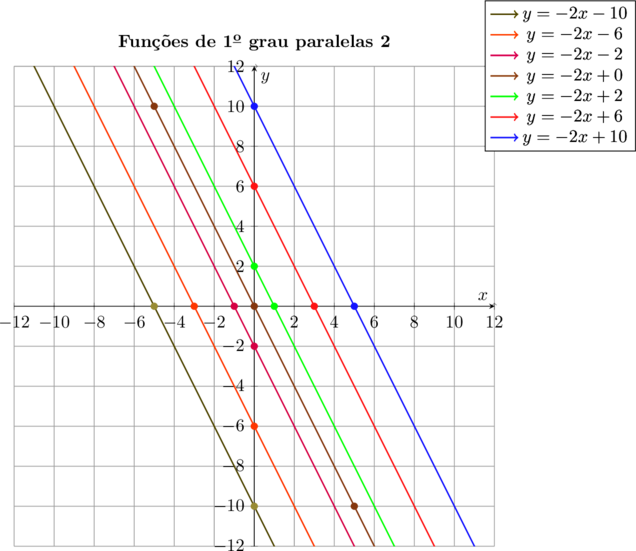
Novamente, temos uma “família” de reta paralelas, que diferem entre si apenas pelo coeficiene linear, que começa em $\color{navy}{-10}$ e termina em $\color{navy}{10}$. Os coeficientes angulares são todos iguais a $\color{navy}{-2}$, inclusive para a função linear que intercepta ambos os eixos na origem do sistema de coordenadas cartesianas.

Você notou que até o momento, não tivemos nenhum caso de reta que fosse paralela ao eixo $\color{maroon}{z}$ ? Ou ao eixo $\color{maroon}{y}$?

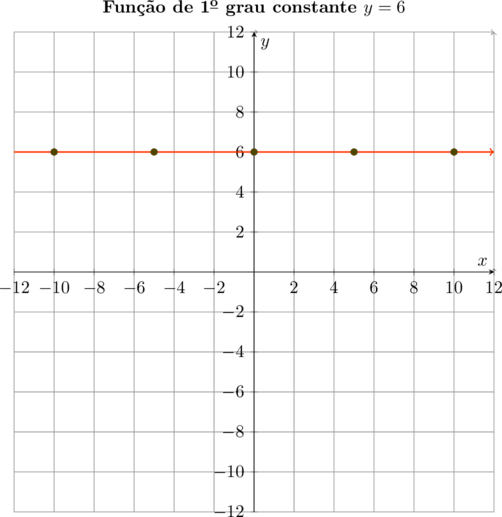
Pois é o que vamos ver agora. Uma função, denominada $\color{brown}{constante}$, tem a forma $\bbox[4px,border:2px solid olive]{\color{navy}{y = b}}$ e o seu gráfico é uma linha reta, paralela ao eixo das $\color{navy}{abcissas}$. Seu coeficiente angular é igual a $\color{navy}{a = 0}$. Vamos tomar como exemplo \[\bbox[4px,border:2px solid olive]{\color{maroon}{y = 6}}\]

para $x = -10 $ $\Rightarrow$ $ y = 6 $ $\rightarrow$ $\color{maroon}{(-10, 6)}$;
para $x = -5 $ $\Rightarrow$ $ y = 6 $ $\rightarrow$ $\color{maroon}{(- 5, 6)}$;
para $x = 0 $ $\Rightarrow$ $ y = 6 $ $\rightarrow$ $\color{maroon}{(0, 6)}$;
para $x = 5 $ $\Rightarrow$ $ y = 6 $ $\rightarrow$ $\color{maroon}{(5, 6)}$;
para $x = 10 $ $\Rightarrow$ $ y = 6 $ $\rightarrow$ $\color{maroon}{(10, 6)}$;

Vamos representar gráficamente.

Rendered by QuickLaTeX.com

E o caso da reta paralela ao eixo $\color{brown}{y}$? Neste caso temos apenas uma relação, pois, para o mesmo valor de $\color{brown}{x}$, temos os valores de $\color{brown}{y}$ $\color{brown}{variando}$ $\color{brown}{entre}$ $\color{brown}{\pm\infty}$. Por exemplo. Se tivermos o valor \[\bbox[4px,border:2px solid olive]{\color{navy}{x = 4}}\] Y poderá assumir qualquer valor no intervalo mostrado acima. Isso implica que não haverá intersecção com o eixo das $\color{naby}{ordenadas}$ e o coeficiente angular será $\color{brown}{a = \pm\infty}$

Tomando o exemplo citado, podemos formar infinitos pares ordenados. Eis alguns deles:

\[\{(4,-10)(4, -6)(4,0)(4,6)(4,10)\}\]. Representando graficamente, fica:

Rendered by QuickLaTeX.com

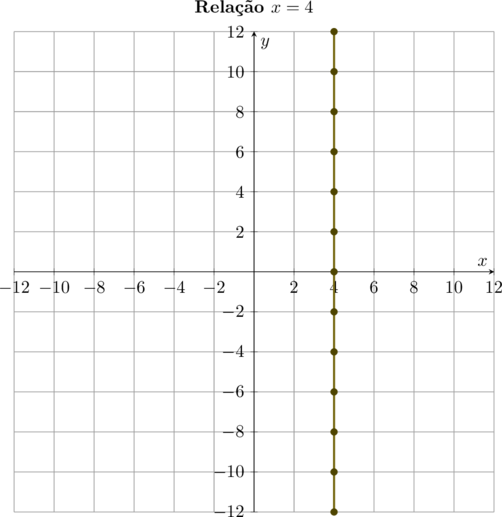
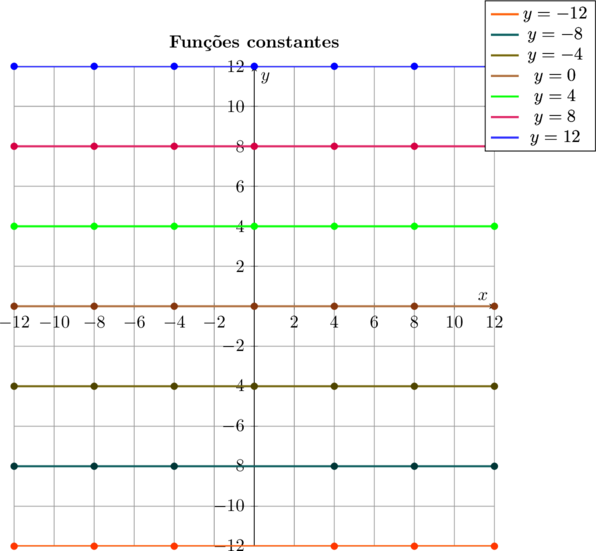
Podemos também traçar uma família de funções constantes no mesmo diagrama, variando os valores da ordenada. Assim podemos fazer:\[\bbox[4px,border:2px solid olive]{\color{brown}{y = -12}}\]

podemos formar os pares ordenados $\color{navy}{\{(-12,-12)(-8,-12)(-4,-12)(0-12)(4,-12)(8,-12)(12,-12)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{y = -8}}\]

podemos formar os pares ordenados $\color{navy}{\{(-12,-8)(-8,-8)(-4,-8)(0-8)(4,-8)(8,-8)(12,-8)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{y = -4}}\]

podemos formar os pares ordenados $\color{navy}{\{(-12,-4)(-8,-4)(-4,-4)(0,-4)(4,-4)(8,-4)(12,-4)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{y = -0}}\]

podemos formar os pares ordenados $\color{navy}{\{(-12,0)(-8,0)(-4,0)(0,0)(4,0)(8,0)(12,0)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{y = 4}}\]

podemos formar os pares ordenados $\color{navy}{\{(-12,4)(-8,4)(-4,4)(0,4)(4,4)(8,4)(12,4)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{y = 8}}\]

podemos formar os pares ordenados $\color{navy}{\{(-12,8)(-8,8)(-4,8)(0,8)(4,8)(8,8)(12,8)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{y = 12}}\]

podemos formar os pares ordenados $\color{navy}{\{(-12,12)(-8,12)(-4,12)(0,12)(4,12)(8,12)(12,12)\}}$

Representando graficamente, fica:

Rendered by QuickLaTeX.com

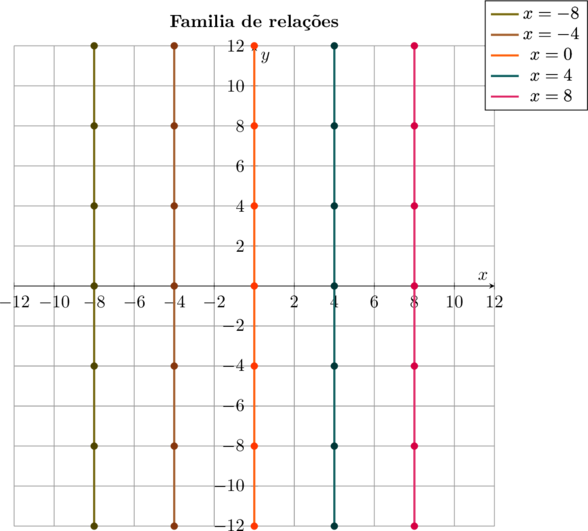
Agora uma família de retas representando relações, em vários pontos do eixo das $\color{navy}{abcissas}$.

\[\bbox[4px,border:2px solid olive]{\color{brown}{x = -8}}\]

Sejam os pares ordenados $\color{navy}{\{(-8, -12) (-8,-8)(-8,-4)(-8,0)(-8,4)(-8,8)(-8,12)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{x = -4}}\]

Sejam os pares ordenados $\color{navy}{\{(-4, -12) (-4,-8)(-4,-4)(-4,0)(-4,4)(-4,8)(-4,12)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{x = 0}}\]

Sejam os pares ordenados $\color{navy}{\{(0, -12) (0,-8)(0,-4)(0,0)(0,4)(0,8)(0,12)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{x = 4}}\]

Sejam os pares ordenados $\color{navy}{\{(4, -12) (4,-8)(4,-4)(4,0)(4,4)(4,8)(4,12)\}}$

\[\bbox[4px,border:2px solid olive]{\color{brown}{x = 8}}\]

Sejam os pares ordenados $\color{navy}{\{(8, -12) (8,-8)(8,-4)(8,0)(8,4)(8,8)(8,12)\}}$

No gráfico cartesiano teremos:

Rendered by QuickLaTeX.com

Usando as funções dadas como base, escreva duas funções paralelas e faça a representação gráfica das mesmas.

a) $\color{olive}{y = {x\over 2} + 4}$

b) $\color{olive}{y = {{- 2x}\over 3} – 1}$

c) $\color{olive}{y = 3} $

d)$\color{olive}{y = -4x + 2}$

e)$\color{olive}{y = 5x – 6}$

f)$\color{olive}{y = \frac{7}{3} {x} + 5}$

g)$\color{olive}{{{y}\over{3}} = 2x – 3}$

h)$\color{olive}{y = 4x + 3}$

Se houver dificuldades na resolução dos exercícios, ou no entendimento do conteúdo, use um dos canais abaixo listados e peça esclarecimentos. Estou à disposição.

Curitiba, 30 de junho de 2016. Melhorado e republicado em 09 de outubro de 2019.

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@AdamsDcio

Telefone: (41) 3019-4760

Celular: (41) 99805-0732