Trigonometria
O nome desse assunto começa com uma palavra bem nossa conhecida trigo, o que pode nos sugerir algo bem diferente do que é na verdade. A origem da palavra trigonometria, vem da língua grega, aquela dos filósofos, matemáticos, geômetras e outras especialidades, que viveram nos tempos antigos, naquele país insular.
Nessa língua temos a palavra trígono, significando três ângulos ou seja triângulo. Na verdade já é uma palavra composta de duas partes: tri = três e gono = ângulo. Já estudamos algumas relações métricas nos triângulos, porém apenas relacionando os lados e as linhas como altura, mediana, bissetriz e mediatriz. Podemos também estabelecer relações entre os lados e os ângulos que eles formam. Esse é o assunto de que iremos falar agora e denomina-se trigonometria.
Trigonometria no triângulo retângulo.
É o estudo das relações existentes entre os ângulos de um triângulo retângulo e seus respectivos lados.
Vejamos como isso funciona.
Temos na figura um triângulo retângulo $\Delta{(ABCA)}$, junto com a sucessão de outros que lhe são semelhantes:
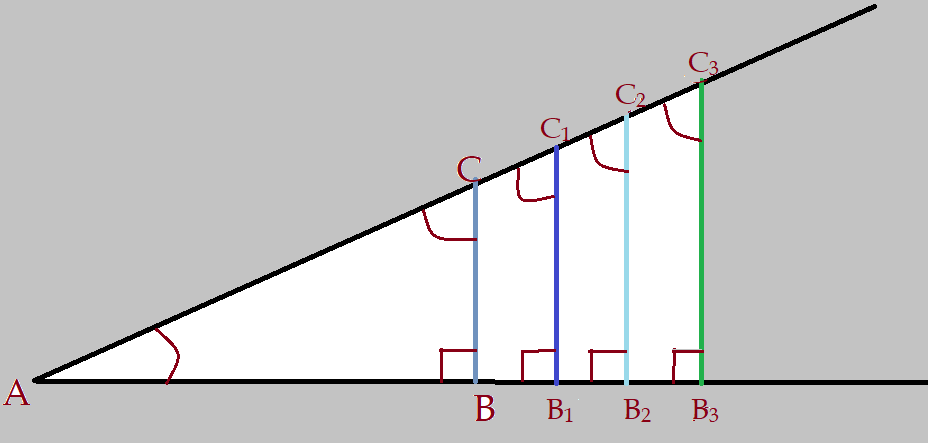
$\Delta{(AB_{1}C_{1}A)} \land\Delta{(AB_{2}C_{2}A)}\land \Delta{(AB_{3}C_{3}A)}$.
São semelhantes por terem todos um ângulo comum no vértice $\hat{A}$; todos têm um ângulo reto nos vértices $\hat{B}, \hat{B_{1}}, \hat{B_{2}}, \hat{B_{3}}$. Como consequência os outros ângulos agudos também são congruentes.
Quando estudamos triângulos semelhantes, vimos que eles têm os lados homólogos proporcionais. São os lados compreendidos entre dois ângulos congruentes nos dois triângulos.
Ao estudar as medidas desses lados, identificou-se a existência de uma razão constante entre os lados que são adjacentes ou opostos aos ângulos. Foi assim que surgiu a trigonometria. Poderíamos traçar uma infinidade de linhas paralelas à $\overline{BC}$, na figura acima e sempre teríamos a mesma proporção entre os respectivos lados.
Observando os triângulos da figura, vemos que os segmentos $\overline{AC}. \overline{AC_{1}}, \overline{AC_{2}}, \overline{AC_{3}}$ são as hipotenusas. Os segmentos $\overline{AB}, \overline{AB_{1}}, \overline{AB_{2}}, \overline{AB_{3}}$ são os catetos adjacentes ao ângulo $\hat{A} = \alpha$ e os segmentos $\overline{BC}, \overline{B_{1}C_{1}}, \overline{B_{2}C_{2}}, \overline{B_{3}C_{3}}$ são os catetos opostos ao mesmo ângulo agudo $\alpha$. As razões entre os lados de um triângulo retângulo, são o que denominamos razões trigonométricas, a saber:
Cosseno: é o quociente do cateto adjacente pela hipotenusa.
Esse valor é constante, para qualquer tamanho do triângulo.
$cos \alpha = \frac{cat. adj.}{hip} = \frac{\overline{AB}}{\overline{AC}} =\frac{\overline{AB_{1}}}{\overline{AC_{1}}} = \frac{\overline{AB_{2}}}{\overline{AC_{2}}} = \frac{\overline{AB_{3}}}{\overline{AC_{3}}}$
Seno é o quociente do cateto oposto ao ângulo pela hipotenusa.
$sen\alpha = \frac{cat. op.}{hip} =\frac{\overline{BC}}{\overline{AC}} = \frac{\overline{B_{1}C_{1}}}{\overline{AC_{1}}}= \frac{\overline{B_{2}C_{2}}}{\overline{AC_{2}}}=\frac{\overline{B_{3}C_{3}}}{\overline{AC_{3}}}$
Tangente é o quociente do cateto oposto ao ângulo, pelo cateto adjacente.
$tg\alpha = \frac{cat. op.}\over{cat. adj.} = \frac{\overline{BC}}{\overline{AB}} =\frac{\overline{B_{1}C_{1}}}{\overline{AB_{1}}} = \frac{\overline{B_{2}C_{2}}}{\overline{AB_{2}}} = \frac{\overline{B_{3}C_{3}}}{\overline{AB_{3}}}$
Co-tangente é o quociente do cateto adjacente pelo cateto oposto do ângulo.
$ctg\alpha = \frac{cat. adj.}{cat. op.} = \frac{\overline{AB}}{\overline{BC}} = \frac{\overline{AB_{1}}}{\overline{B_{1}C_{1}}}=\frac{\overline{AB_{2}}}{\overline{B_{2}C_{2}}} = \frac{\overline{AB_{3}}}{\overline{B_{3}C_{3}}}$
Se observarmos bem, notaremos que a Co-tangente é igual ao inverso da tangente, o que podemos exprimir assim:
$ctg\alpha = \frac{1}{tg\alpha}$
Mais uma relação entre as razões trigonométricas:
$cos\alpha = {\overline{AB}\over\overline{AC}}$$\Leftrightarrow$$\overline{AB} = {\overline{AC}\cdot {cos\alpha}}$
$sen\alpha =\frac{\overline{BC}}{\overline{AC}}$$\Leftrightarrow$$\overline{BC} = {\overline{AC}\cdot {sen\alpha}}$
$tg\alpha = \frac{\overline{BC}}{\overline{AB}}=\frac {{\overline{AC}\cdot sen\alpha}}{\overline{AC}\cdot {cos\alpha}}$
$tg\alpha = \frac{sen\alpha}{cos \alpha}$
Como vimos a tangente e a co-tangente são uma o inverso da outra. Isso nos permite concluir que:
$ctg\alpha = \frac{cos\alpha} {sen\alpha}$
Ainda existem duas outras razões trigonométricas. São elas a cossecante e a secante.
Cossecante é a denominação dada ao inverso do seno.
$csc\alpha =\frac {1}{sen\alpha}$
Equivale a $csc\alpha = \frac{hipotenusa}{cateto oposto}$
Secante é o inverso do cosseno de um ângulo.
$sec\alpha = \frac{1}{cos\alpha}$
Equivale a $sec\alpha = {{hipotenusa}\over{cateto adjacente}}$
Relação fundamental da trigonometria.
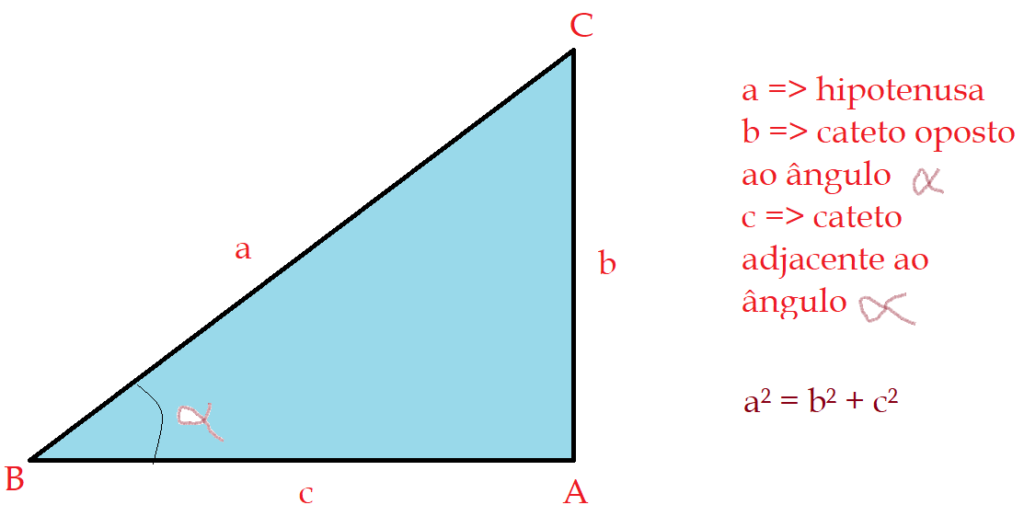
Lembrando do estudo do triângulo retângulo, encontramos o Teorema de Pitágoras.
Vamos aplicar as definições das razões trigonométricas seno e cosseno ao triângulo acima.
$sen\alpha =\frac{c}{a}$$\Leftrightarrow$$ c = {a\cdot sen\alpha} $
$cos\alpha = \frac{b}{a}$$\Leftrightarrow$$b = {a\cdot cos\alpha}$
$a^2 = b^2 + c^2$$\Leftrightarrow$$a^2 ={(a\cdot cos\alpha)}^2 + {(a\cdot sen\alpha)}^2$
Distribuindo o expoente dos termos do segundo membro da igualdade, teremos:
$a^2 = {a^2\cdot cos^2\alpha} + {a^2\cdot sen^2\alpha}$
Cancelando o fator comum a todos os termos $a²$, chegaremos à relação fundamental.
$1 = sen^2\alpha + cos^2\alpha$
Essa relação fundamental é, de certa forma, o equivalente trigonométrico do Teorema de Pitágoras. É denominada fundamental pela importância de suas aplicações no desenvolvimento de múltiplos raciocínios dentro do assunto.
É escusado dizer que os valores das razões trigonométricas são em sua quase totalidade representadas por números decimais. Não se pode ter a pretensão de guardar de memória tal quantidade de informações. Para isso existem as tabelas trigonométricas e o mais fácil é fazer uso de calculadoras eletrônicas para obter esses valores. Em geral usamos arredondar com duas ou três casas decimais, obedecendo os critérios de arredondamento.
Os valores mais comuns são escritos na forma de razões, onde algumas contém um termo irracional (radical).
| $sen\alpha$ | $cos\alpha$ | $tg\alpha$ | $ctg\alpha$ | $csc\alpha$ | $sec\alpha$ | |
| $0^{0}$ | $0$ | $1$ | $0$ | 4$\infty$ | $\infty$ | $1$ |
| $30^{04}$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{3}}{3}$ | $\sqrt{3}$ | $2$ | $\frac{2\sqrt{3}}{3}$ |
| $45^{0}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $1$ | $1$ | $\sqrt{2}$ | $\sqrt{2}$ |
| $60^{0}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ | $\sqrt{3}$ | $\frac{\sqrt{3}}{3}$ | $\frac{2\sqrt{3}}{3}$ | $2$ |
| $90^{0}$ | $1$ | $0$ | $\infty$ | $0$ | $1$ | $\infty$ |
| $120^{0}$ | $\frac{\sqrt{3}}{2}$ | $-\frac{1}{2}$ | $-\sqrt{3}$ | $-\frac{\sqrt{3}}{3}$ | $\frac{2\sqrt{3}}{3}$ | $-2$ |
| $135^{0}$ | $\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-1$ | $-1$ | $\sqrt{2}$ | $-\sqrt{2}$ |
| $150^{0}$ | $\frac{1}{2}$ | $-\frac{\sqrt{3}}{2}$ | $- \frac{\sqrt{3}}{3}$ | $-\sqrt{3}$ | $2$ | $-\frac{2\sqrt{3}}{3}$ |
| $180^{0}$ | $0$ | $-1$ | $0$ | $-\infty$ | $\infty$ | $-1$ |
Atenção! Observe bem a tabela acima e verifique um detalhe importante. Definimos as razões entre os lados de um triângulo retângulo. Como foi visto na ocasião do estudo dos triângulos, a soma dos ângulos internos de um triângulo é sempre igual a $180^{0}$. Então, se um dos ângulos é reto, $\alpha = 90^{0}$, teremos que a soma dos outros dois ângulos, que são agudos obrigatoriamente, será igual a $\beta + \zeta = 90^{0}$. Fica fácil verificar que o seno de um dos ângulos agudos é igual ao cosseno do outro, que é seu complemento.
$sen(60º) = cos(90º – 60º) = cos(30º)$
Isso equivale a afirmar que “o seno de um ângulo é igual ao cosseno de seu complemento”
Há ainda outras igualdades que podemos inferir pela análise da tabela trigonométrica.
Exercícios
01. Um triângulo retângulo, tem a hipotenusa medindo $a = 15,0 cm$ e um de seus ângulos agudos mede $\zeta = 30^{0}$. Determine as medidas dos catetos oposto e adjacente, bem como a medida do outro ângulo agudo.
$sen\beta = {b\over a}$$\Leftrightarrow$$ sen(30^{0}) = {b\over{15,0}}$
$b = {{15,0}\cdot {1\over2}}$$\Leftrightarrow$$b = 7,5 cm$
$cos\beta = {c\over a}$$\Leftrightarrow$$ {\sqrt{3}\over2} = {c\over{15,0}}$
$c = {{15,0}\cdot{\sqrt{3}\over2}}$$\Leftrightarrow$$ c = (7,5)\cdot\sqrt{3}cm$
Se um ângulo agudo mede $\beta = 30^{0}$ o outro medirá:
$\zeta = {90^{0} – 30^{0}} = 60^{0}$
02. Um triângulo retângulo tem em um de seus ângulos agudos $cos\beta =\frac{ \sqrt{5}}{5}$. Determine o valor do seno desse mesmo ângulo. Depois obtenha os valores da tangente, cotangente, cossecante e secante.
Iremos começar pela aplicação da relação fundamental para determinar o valor do seno.
$sen^2\beta + cos^2\beta = 1$$\Leftrightarrow$$sen^2\beta + \left(\frac{\sqrt{5}}{5}\right)^2 = 1$
$sen^2\beta = 1 – \left(\frac{\sqrt{5}}{5}\right)^2$$\Leftrightarrow$$ sen^2\beta = 1 – \frac{5}{25}$
$sen^2\beta = \frac{ 5 – 1}{5} = \frac{4}{5}$
$sen\beta = \sqrt{\frac{4}{5}}$$\Leftrightarrow$$sen\beta = {2\over\sqrt{5}}$
$sen\beta= \frac{2\cdot\sqrt{5}}{5}$
$tg\beta = \frac{sen\beta}{cos\beta}$$\Leftrightarrow$$tg\beta = {\left(\frac{\frac{2\cdot\sqrt{5}}{5}}{\frac{\sqrt{5}}{5}}\right)}$
$tg\beta = \frac{2\cdot\sqrt{5}}{5}\cdot\frac{5}{\sqrt{5}}$$\Leftrightarrow$$tg\beta= 2$
$tg\beta= 2$
$ctg\beta = \frac{1}{tg\beta}$$\Leftrightarrow$$ctg\beta = \frac{1}{2}$
$ctg\beta =\frac {1}{2}$
$csc\beta = \frac{1}{sen\beta}$$\Leftrightarrow$$csc\beta =\frac {1}{\frac{2\sqrt{5}}{5}}} = \frac{5}{2\sqrt{5}} $
$csc\beta = \frac{5\cdot\sqrt{5}}{2\cdot\sqrt{5}^2} = \frac{5\cdot\sqrt{5}}{10} = \frac{\sqrt{5}}{2}$
$csc\beta = \frac{\sqrt{5}}{2}$
$sec\beta = \frac{1}{cos\beta}$$\Leftrightarrow$$sec\beta= {1}\cdot \frac{5}{\sqrt{5}}$
$sec\beta = \frac{{5}\cdot\sqrt{5}}{\sqrt{5}^2}$
$sec\beta = \frac{\not{5}}{\not{5}}\cdot\sqrt{5}$
$sec\beta = \sqrt{5}$
03. Os catetos de um triângulo retângulo medem respectivamente $b = 8,0 cm$ e $c = 6,0 cm$. Determine: a) a tangente e a cotangente do ângulo agudo $\gamma$ formado pela hipotenusa e o cateto b; b) o seno e o cosseno desse mesmo ângulo; c) a secante e a cossecante desse ângulo; d) a medida da hipotenusa.
a)Sendo sendo os catetos os segmentos $b$ e $c$, temos que a tangente será dada por:
$tg\gamma = \frac{c}{b}$$\Leftrightarrow$$tg\gamma = \frac{6,0}{8,0} =\frac {3}{4}$
$tg\gamma = \frac{3}{4}$
$ctg\gamma = \frac{b}{c}$$\Leftrightarrow$$ctg\gamma = \frac{8,0}{6,0} = \frac{4}{3}$
$ctg\gamma = \frac{4}{3}$
b)Temos que
$sen^2\gamma + cos^2\gamma = 1$
Podemos dividir a expressão toda por $cos^2\gamma$
$\frac{sen^2\gamma}{cos^2\gamma} +\frac{cos^2\gamma}{cos^2\gamma} = \frac{1}{cos^2\gamma}$
Daí tiramos que:
$tg^2\gamma + 1 =\frac {1}{cos^2\gamma}$$\Leftrightarrow$$cos^2\gamma = \frac{1}{tg^2\gamma +1}$
$cos^2\gamma =\left[\frac{1}{\left(\frac{3}{4}\right)^2 + 1}\right]$ =$\left[\frac{1}{\left(\frac{9}{16}\right)+1}\right]$
$ cos^2\gamma = \left[\frac{1}{\left(\frac{9 + 16}{16}\right)}\right]$
$cos^2\gamma = \left[\frac{1}{\left(\frac{25}{16}\right)}\right] = \frac{16}{25}$
$\sqrt{cos^2\gamma} = \sqrt{\left(\frac{16}{25}\right)} =\frac {4}{5}$
$cos\gamma = \frac{4}{5} = 0,8$
Com procedimento semelhante teremos:
$sen^2\gamma + cos^2\gamma = 1$$\Leftrightarrow$$\frac{sen^2\gamma}{sen^2\gamma} + \frac{cos^2\gamma}{sen^2\gamma} = \frac{1}{sen^2\gamma}$
$ 1 + ctg^2\gamma = \frac{1}{sen^2\gamma}$$\Leftrightarrow$$sen^2\gamma = \left[\frac{1}{ 1 + cotg^2\gamma}\right]$
$sen^2\gamma = \left[\frac{1}{1 + (\frac{4}{3})^2}\right]$$\Leftrightarrow$$sen^2\gamma = \left[\frac{1}{1 +\frac{16}{9}}\right]$
$sen^2\gamma = \left[\frac{1}{\frac{9 + 16} {9}}\right]$$\Leftrightarrow$$sen^2\gamma = \left[\frac{1}{\frac{25}{9}}\right]$
$\sqrt{sen^2\gamma} = \left[\sqrt{\frac{9}{25}}\right]$$\Leftrightarrow$$sen\gamma = \frac{3}{5} = 0,6$
$sen\gamma = \frac{3}{5} = 0,6$
c) a cossecante é $csc\gamma =\frac{1}{sen\gamma}$
$csc\gamma = \left[\frac{1}{\left(\frac{3}{5}\right)}\right]$
$csc\gamma =\frac{5}{3}$
A secante é $sec\gamma = \frac{1}{cos\gamma}$
$sec\gamma = \left[\frac{1}{\left(\frac{4}{5}\right)}\right]$
$sec\gamma = \frac{5}{4}$
d)a hipotenusa pode ser obtida de diversas formas. Vamos determiná-la a partir do seno do ângulo.
$sen\gamma =\frac {c}{a}$$\Leftrightarrow$$a = \frac{c}{sen\gamma}$
$a = \left[\frac{6,0}{\frac{3}{5}}\right]$$\Leftrightarrow$$a = \left[\frac{6,0\cdot 5}{3}\right]$
$a = \frac{30,0}{3}$
$a = 10,0 cm$
Exercícios para resolver.
01. Em um triângulo retângulo a hipotenusa mede 12,0 cm e um dos ângulos agudos adjacentes mede $\beta = 60^{0}$. Determine o seno do outro ângulo agudo, a tangente e a cotangente desse ângulo. Depois calcule as medidas dos dois catetos.
02. Em um triângulo retângulo sabe-se que a hipotenusa $a = 7\sqrt{2} cm$ e um dos catetos mede $b = 8,0 cm$. Determine o seno e cosseno do ângulo formado, a medida do outro cateto, as razões tangente, cotangente, secante e cossecante do ângulo.
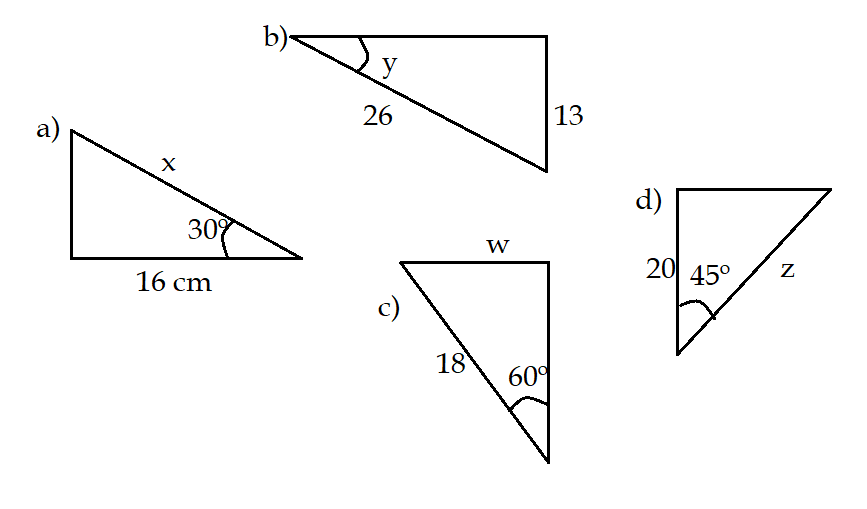
03. Determine os valores de ${x}, {y}, {w}, {z}$ em cada caso:
04. Em um triângulo retângulo, determine as medidas dos ângulos agudos e da hipotenusa, sabendo que um dos catetos mede $b = 3,0 cm$ e o outro mede$\sqrt{3} cm$.
05. (Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de $30^{0}$ com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:
a) $6\sqrt{3}cm$
b) $12 m$
c) $13,6 m$
d) $9\sqrt{3} m$
e) $18 m$
06. (UFAM) Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é:
a) $2\sqrt{3}$
b) ${\sqrt{3}\over3}$
c) ${\sqrt{3}\over6}$
d) ${\sqrt{20}\over{20}}$
e) $3\sqrt{3}$
07. Uma pessoa observa um edifício de 270 m de altura, sob um ângulo de $30^{0}$ em relação à horizontal. Admitindo que o olho desse observador encontra-se no nível do chão, qual é a distância entre o edifício e o observador?
08. Um poste de iluminação tem 10 m de altura e em dado instante projeta uma sombra de 12 m. Determine as razões trigonométricas do ângulo de incidência dos raios solares em relação ao solo.
09. Uma corda é amarrada no topo de uma árvore que está para ser removida, mas precisa ser puxada para cair na posição em que não irá causar danos. Se a altura em que a corda é amarrada é de 15 m, determine o comprimento da corda para que ela não atinja os trabalhadores encarregados ao cair. O tronco será cortado rente ao chão.
10. Uma escada é construída entre dois andares de uma edificação. A altura entre os dois andares é de 3,0 m e a distância horizontal entre o primeiro pé do primeiro degrau e a soleira do andar superior é de 3,5 m. Determine a medida da escada do ponto em que ela começa e onde termina. Qual é o ângulo de inclinação da escada em relação à vertical?
11. (Vunesp) O cosseno do menor ângulo interno de um triângulo retângulo é $\frac{\sqrt{3}}{2}$. Se a medida da hipotenusa desse triângulo é 4 unidades, então é verdade que um dos catetos desse triângulo mede, na mesma unidade,
a)$ 1$
b) $\sqrt{3}$
c) $2$
d) $3$
e) $\frac{\sqrt{3}}{3}$
11. (FGV) Na figura a seguir, o segmento BD é perpendicular ao segmento AC.
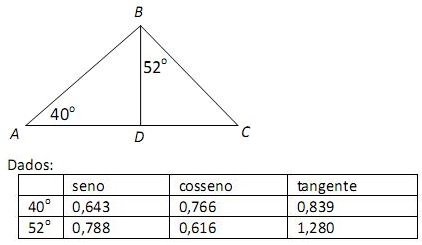
Se AB = 100m, um valor aproximado para o segmento DC é:
a) 76 m;
b) 62 m;
c) 68 m;
d) 82 m;
e) 90 m.
13. (FGV) A plateia de um teatro, vista de cima para baixo, ocupa o retângulo ABCD da figura a seguir, e o palco é adjacente ao lado BC. As medidas do retângulo são AB = 15m e BC = 20m.
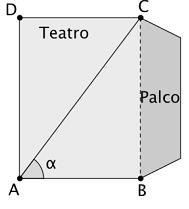
Um fotógrafo que ficará no canto A da plateia deseja fotografar o palco inteiro e, para isso, deve conhecer o ângulo da figura para escolher a lente de abertura adequada.
O cosseno do ângulo da figura acima é:
a) 0,5
b) 0,6
c) 0,75
d) 0,8
e) 1,33
14. (Unoesc) Um homem de 1,80 m encontra-se a 2,5 m de distância de uma árvore, conforme ilustração a seguir. Sabendo-se que o ângulo α é de $42^{0}$, determine a altura dessa árvore.
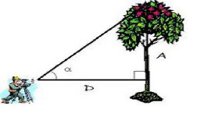
Use:
$Seno 42^{0} = 0,669$
$Cosseno 42^{0} = 0,743$
$Tangente de 42^{0} = 0,90$
a) 2,50 m;
b) 3,47 m;
c) 3,65 m;
d) 4,05 m;
e) Nda.
15. (Enem-2013) As torres Puerta de Europa são duas torres inclinadas uma contra a outra, construídas numa avenida de Madri, na Espanha. A inclinação das torres é de 15° com a vertical e elas têm, cada uma, uma altura de 114 m (a altura é indicada na figura como o segmento AB). Estas torres são um bom exemplo de um prisma oblíquo de base quadrada e uma delas pode ser observada na imagem.

Disponível em: www.flickr.com. Acesso em: 27 mar. 2012.
Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço:
a) $ A< 100 m^2$;
b) $ 100m^2<A<300m^2$;
c) $ 300m^2<A<500m^2$;.
d) $ 500 m^2<A<700 m^2;
e) $A > 700 m^2$.
Se existirem dúvidas sobre a solução dos exercícios ou sobre o conteúdo teórico, peça ajuda por um dos canais abaixo listados.
Curitiba, 23 de novembro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

