Relações entre as razões trigonométricas.
Já vimos no post anterior as primeiras relações e iremos recordá-las agora, para depois complementar com mais algumas e resolver exercícios de aplicação.
- Relação fundamental
$\color{green}{sen^{2}\beta + cos^2\beta = 1}$
- tangente e cotangente
$\color{green}{tg\beta = {{sen\beta}\over{cos\beta}}}$
$\color{green}{ctg\beta = {{cos\beta}\over{sen\beta}}}$
- cossecante e secante
$\color{green}{csc\beta = {1\over{sen\beta}}}$
$\color{green}{sec\beta = {1\over{cos\beta}}}$
Novas relações tiradas da fundamental
Dividindo a relação fundamental por $\color{red}{sen^2\beta}$ teremos:
${{sen^2\beta}\over{sen^2\beta}} + {{cos^2\beta}\over{sen^2\beta}} = {1\over{sen^2\beta}}$
Lembrando que $\color{navy}{{{cos\beta}\over{sen\beta}} = ctg\beta}$
$ {1 + ctg^2\beta = csc^2\beta}$$\Leftrightarrow$${\sqrt{csc^2\beta} = \sqrt{1 + ctg^2\beta}}$
$\color{maroon}{csc\beta = \sqrt{1 + ctg^2\beta}}$
Seguindo o mesmo raciocínio, agora dividindo a relação fundamental por $cos^2\beta$, e substituindo as razões equivalentes.
${{sen^2\beta}\over{cos^2\beta}} + {{cos^2\beta}\over {cos^2\beta}} = {1\over {cos^2\beta}}$$\Leftrightarrow$$ tg^2\beta + 1 = sec^2\beta$
${\sqrt{sec^2\beta} = \sqrt{1 + tg^2\beta}}$
$\color{maroon}{sec\beta = \sqrt{1 + tg^2\beta}}$
Em $tg\beta = {{sen\beta}\over{cos\beta}}$, isolando $sen\beta$ e substituindo na relação fundamental.
$\color{Brown}{sen\beta = {tg\beta}\cdot{cos\beta}}$
${tg^2\beta}\cdot{cos^2\beta} + cos^2\beta = 1$$\Leftrightarrow$$cos^2\beta\cdot{(tg^2\beta + 1)} = 1$
$cos^2\beta = {1\over{tg^2\beta + 1}}$$\Leftrightarrow$$\sqrt{cos^2\beta} = \sqrt{1\over{tg^2\beta + 1}}$
$cos\beta = \sqrt{1\over{tg\beta+1}}$
$\color{maroon}{cos\beta = \left({tg^2\beta + 1} \right) ^{-{1\over2}}}$
Procedendo da mesma forma com $ctg\beta = {{cos\beta}\over{sen\beta}}$
${ctg\beta}\cdot{sen\beta} = cos\beta $
$sen^2\beta + ({ctg\beta}\cdot{sen\beta})^2 = 1$
$sen^2\beta + {ctg^2\beta}\cdot{sen^2\beta} = 1$
$sen^2\beta\cdot({1 + ctg^2\beta}) = 1$$\Leftrightarrow$$ sen^2\beta = {1\over{1 + ctg^2\beta}}$
$\sqrt{sen^2\beta} = \sqrt{1\over{1 + ctg^2\beta}}$$\Leftrightarrow$$sen\beta = {1\over\sqrt{ctg^2\beta + 1}}$
$\color{maroon}{sen\beta = \left({ctg^2\beta + 1}\right)^{-{1\over 2}}}$
Lei dos senos.
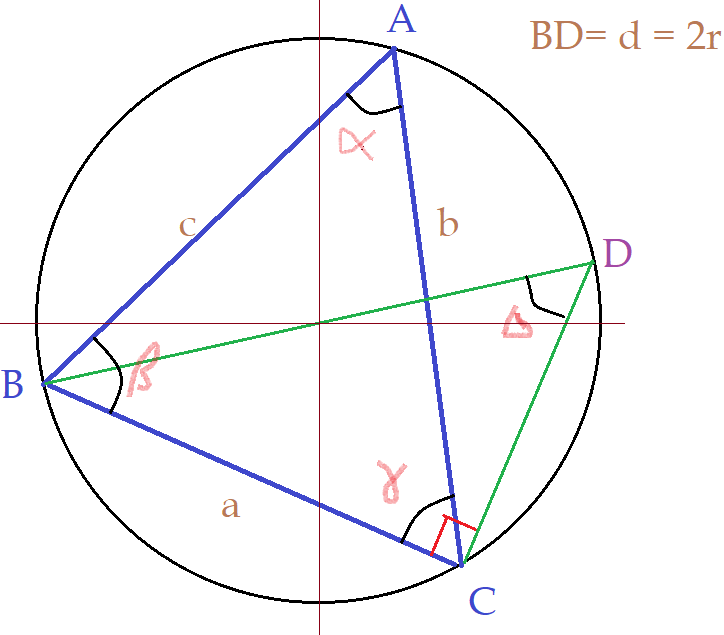
O triângulo $\Delta{BCDB}$ é retângulo no vértice $C$. O segmento $\overline{BC}$ é cateto oposto ao ângulo $\Delta$. Por isso:
$sen\Delta = {a\over \overline{BD}} = {a\over{2r}}$
$\color{Violet}{{a\over sen\Delta} = 2r}$
O vértice $\hat{A}$ é subtendido pelo mesmo arco $\hat{BC}$ assim como acontece com o ângulo $\Delta$. Donde se conclui que:
${{a\over sen\alpha} = 2r}$
Aplicando o mesmo raciocínio aos outros ângulos, teremos:
${{b\over sen\beta} = 2r}$
${{c\over sen\gamma} = 2r}$
Como consequência podemos estabelecer a lei dos cossenos, cujo enunciado fica assim:
Em qualquer triângulo o lado é diretamente proporcional ao seno do ângulo oposto e a razão constante é igual ao diâmetro da circunferência circunscrita.
$\color{maroon}{{a\over sen\alpha} = {b\over sen\beta} = {c\over sen\gamma} = 2r}$
Essa lei é especialmente útil na determinação dos demais elementos de um triângulo, conhecendo-se um ângulo e dois lados.
Leis dos cossenos
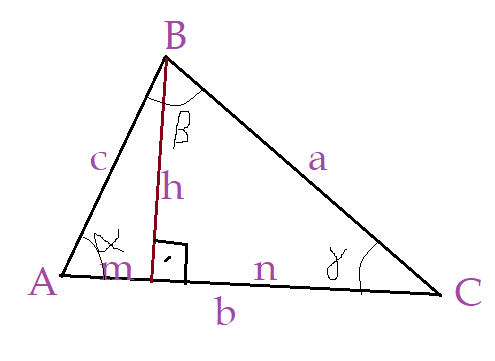
Vamos aplicar o Teorema de Pitágoras nos dois triângulos retângulos formados pela altura $h$ em relação ao lado $b$
$a^2 = h^2 + n^2$ (I)
${c^2 = h^2 + m^2}$$\Leftrightarrow$${h^2 = c^2 – m^2}$ (II)
${h^2 = c^2 – m²}$ (II)
Temos que ${b = m + n}$$\Leftrightarrow$${n = b – m}$
${n = b – m}$ (III)
${{m\over c} = cos\alpha}$$\Leftrightarrow$${m = c\cdot cos\alpha}$
${m = c\cdot cos\alpha}$ (IV)
Substituindo (II), (III) e (IV) em (I), teremos:
$a^2 = {c^2 – m^2} + {(b – m)^2}$$\Leftrightarrow$$a^2= {c^2 – \left({c\cdot cos\alpha}\right)^2} + {b^2 – 2bm + m^2}$
$a^2 = c^2 – c^2\cdot cos^2\alpha + b^2 -2b\left(c\cdot cos\alpha\right) +\left({c\cdot cos\alpha}\right)^2$
Cancelando os termos simétricos e ordenando a expressão:
$a^2 = b^2 + c^2 – c^2cos^2\alpha – 2bc\cdot cos\alpha + c^2\cdot cos^2 \alpha$
$\color{maroon}{a^2= b^2 + c^2-2bc\cdot cos\alpha}$
Aplicando o mesmo raciocínio em relação aos outros ângulos, teremos:
$\color{maroon}{b^2 = a^2 + c^2 – 2ac\cdot cos\beta}$
$\color{maroon}{{c^2 = a^2 + b^2 – 2ac\cdot cos\gamma}}$
O quadrado da medida de um lado de um triângulo qualquer é igual a soma dos quadrados dos outros lados, menos o duplo produto desses lados pelo cosseno do ângulo por eles formado.
Exercícios
01. A $csc\beta = {{3\sqrt{3}}\over5}$. Determine as demais razões trigonométricas desse mesmo ângulo.
Temos vários caminhos que nos levam aos resultados buscados. Vamos começar pela relação entre cossecante e cotangente.
$csc\beta = {\sqrt{1 + ctg^2\beta}}$
Substituindo e elevando ao quadrado teremos:
$\left({3\sqrt{3}\over5}\right)^2 = {\left({\sqrt{1 + ctg^2\beta}}\right)^2}$
$ {{9\cdot 3}\over{25}}= {1 + ctg^2\beta}$$\Leftrightarrow$${{27}\over{25}} – 1 = ctg^2\beta $
${{27 – 25}\over{25}} = ctg^2\beta$$\Leftrightarrow$$ctg^2\beta = {2\over{25}} $
$\sqrt {ctg^2\beta} = {\sqrt{2\over{25}}}$
$\color{maroon}{ctg\beta= {\sqrt{2}\over 5}}$
Temos que $tg\beta = {1\over ctg\beta}$, o que nos fornece:
$tg\beta =\left[ {1\over\left({\sqrt{2}\over5}\right)}\right]$$\Leftrightarrow$$tg\beta = \left({5\over\sqrt{2}}\right)$
Racionalizando: $ tg\beta =\left({{5\cdot\sqrt{2}}\over\sqrt{2}²}\right)$
$\color{maroon}{tg\beta= {5\sqrt{2}\over 2}}$
Se $\color{navy}{sec\beta = \sqrt{1 + tg^2\beta}}$
$sec\beta =\left[{\sqrt{1 +\left({5\sqrt{2}\over2}\right)^2}}\right]$$\Leftrightarrow$$sec\beta =\left[\sqrt{1 + {{{25}\cdot 2}\over4}}\right]$
$sec\beta = \left[\sqrt{1 + {{25}\over2}}\right]$$\Leftrightarrow$$sec\beta = \left[\sqrt{{2 + 25}\over 2}\right]$
$sec\beta =\left[\sqrt{{27}\over2}\right]$$\Leftrightarrow$$sec\beta= \left[\sqrt{{3^2\cdot 3}\over2}\right]$
$sec\beta = {3\cdot{\sqrt{3}}\over\sqrt{ 2}}$$\Leftrightarrow$$sec\beta = {{3\sqrt{6}}\over 2}$
$\color{maroon}{sec\beta = {{3\sqrt{6}}\over 2} }$
$sec\beta = {1\over cos\beta}$$\Leftrightarrow$$ cos\beta = {1\over sec\beta}$
$cos\beta = {1\over{{3\sqrt{6}}\over2}}$$\Leftrightarrow$$cos\beta = {2\over {3\sqrt{6}}}$
$cos\beta= {{{2\cdot\sqrt{6}}\over{3\cdot{\sqrt{6}}^2}}}$$\Leftrightarrow$$cos\beta = {{2\sqrt{6}}\over{3\cdot 6}}$
$\color{maroon}{cos\beta = {\sqrt{6}\over 9}}$
$csc\beta = {1\over sen\beta}$$\Leftrightarrow$$sen\beta = \left[{1\over\left({3\sqrt{3}\over5}\right)}\right]$
$sen\beta = {5\over{3\sqrt{3}}}$$\Leftrightarrow$$sen\beta = {{5\cdot\sqrt{3}}\over{3\sqrt{3}^2}}$
$\color{maroon}{sen\beta = {5\sqrt{3}\over9}}$
02. Um triângulo tem o lado $a = 8,0\, cm$, um ângulo adjacente a ele mede $\beta = 45^{0}$ e o triângulo está inscrito em uma circunferência de raio $r = 8,0\, cm$. Pede-se determinar as medidas dos outros dois lados e os ângulo $\alpha$ e $\gamma$.
Dados: $a = 8,0\, cm$; $\beta = 45^{0}$ e $r = 8,0\, cm$.
Lei dos senos: ${a\over sen\alpha} = {b\over sen\beta} = {c\over sen\gamma} = {2\cdot r}$
${a\over sen\alpha} = {2\cdot r}$$\Leftrightarrow$$sen\alpha = {a\over 2r}$
$sen\alpha = {8\over{2\cdot 8,0}}$$\Leftrightarrow$$sen\alpha ={1\over2}$
$sen\alpha = {1\over 2}$
$\color{maroon}{\alpha = 30^{0}}$
${b\over sen\beta} = {a\over sen\alpha}$$\Leftrightarrow$${b\over sen {45º}} = {8,0\over sen {30^{0}}}$
${b\over{\sqrt{2}\over 2}} = {8\over {1\over2}}$$\Leftrightarrow$$b = 8\cdot \frac{2\cdot\sqrt{2}}{2}$
$\color{maroon}{b = {8\cdot\sqrt{2}}cm}$
$\alpha + \beta + \gamma = 180^{0}$$\Leftrightarrow$$ 30^{0} + 45^{0} + \gamma = 180^{0}$
$\gamma = 180^{0} – 75^{0}$$\Leftrightarrow$$\gamma = 105^{0}$
$\color{maroon}{\gamma = 105^{0}$
${c\over sen\gamma} = 2\cdot r$
${c\over sen{(45^{0} + 60^{0})}} = 2\cdot 8 $
$\left[{c\over{(sen 45^{0}\cdot cos 60^{0} + sen 60^{0}\cdot cos 45^{0})}}\right] = 16$
$\left[{c\over{{(\sqrt{2}\over2}\cdot {1\over2}} +{{\sqrt{3}\over2}\cdot {\sqrt{2}\over2})}}\right] = 16$
$\left[{c\over{(\sqrt{2}\over 4} +{\sqrt{6}\over 4})}\right] = 16$$\Leftrightarrow$$\left[{c\over{{\sqrt{2} + \sqrt{6}}\over 4}}\right] = 16$
$c = 16\cdot{{\sqrt{2} + \sqrt{6}}\over 4}$
$\color{maroon}{c = 4\cdot\left[{\sqrt{2} + \sqrt{6}}\right] cm}$
Soma de ângulos, seno e cosseno
Imagine se deparar com uma expressão como essa: $y = sen{(\alpha + \beta)}$! ou então $y = cos{(\alpha + \beta)}$!
Simplesmente irá fazer a adição dos ângulos? Isso estará correto? No final do exercício dois acima foi usado esse recurso para obter um dos senos dos ângulos. E não foi assim. Há uma forma mais fácil de resolver essas situações.
Vejamos a demonstração de como fica essa questão. Essa demonstração normalmente não é cobrada do candidato ou aluno em provas, mas eu tenho uma aversão radical à simplesmente despejar uma fórmula e dizer apenas “é assim que se faz”. Sempre quero mostrar o “porquê?” Então me empenho em colocar tudo em pratos limpos.
Vamos inciar por desenhar um retângulo e um triângulo retângulo cuja hipotenusa é a diagonal, à qual iremos atribuir a medida de uma unidade de comprimento.
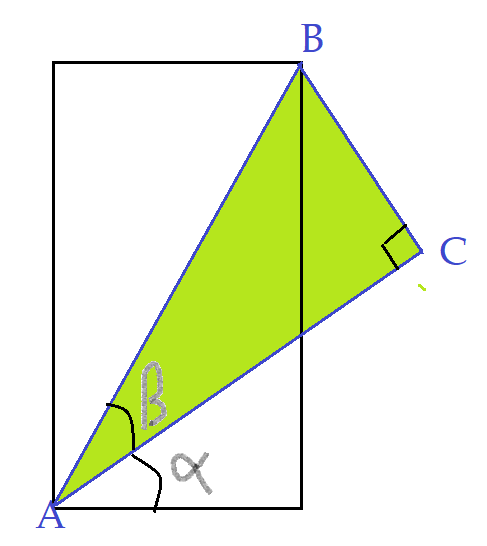
Vamos baixar uma perpendicular ao prolongamento da base do retângulo, a partir do vértice $C$ do triângulo.
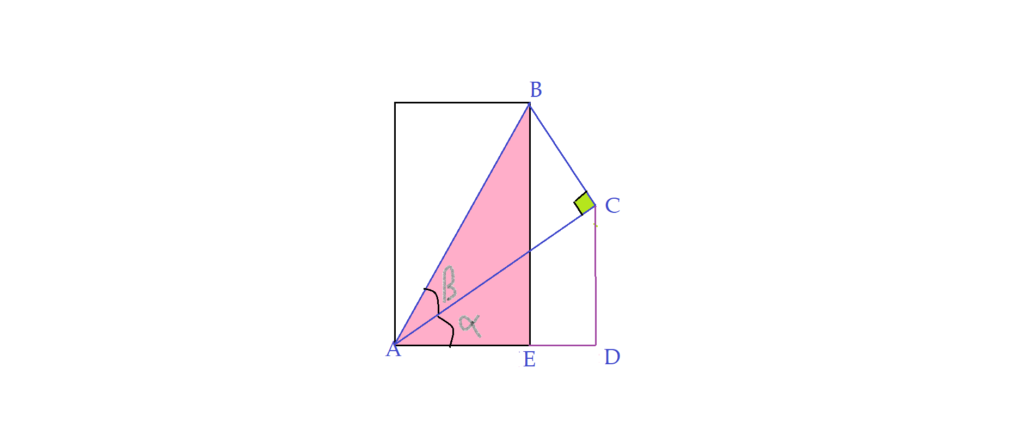
No triângulo $\Delta{ABEA}$, o ângulo do vértice $A$ é igual a soma dos ângulos agudos $\alpha + \beta$ dos outros dois triângulos e podemos escrever, pela definição das razões trigonométricas:
$sen{(\alpha + \beta)} = {{\overline{BE}}\over\overline{AB}}$ (I)
$cos{(\alpha + \beta)} = {{\overline{AE}}\over\overline{AB}}$ (II)
Vamos destacar o triângulo $\Delta{ACDA}$ e analisar as razões seno e cosseno.
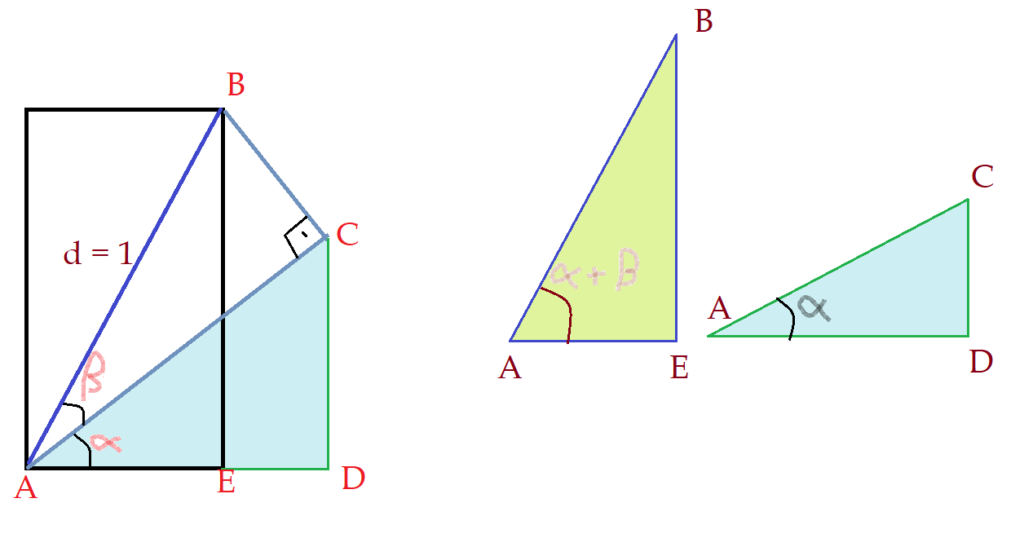
Observando seus lados, temos:
$sen\alpha = {{\overline{CD}}\over\overline{AC}}$
$sen\alpha\cdot\overline{AC} = \overline{CD}$ (III)
$cos\alpha = {{\overline{AE}}\over\overline{AC}}$
$cos\alpha\cdot\overline{AC} = \overline{AE}$ (IV)
Agora vamos destacar o triângulo $\Delta{ABCA}$ e analisar as razões seno e cosseno.
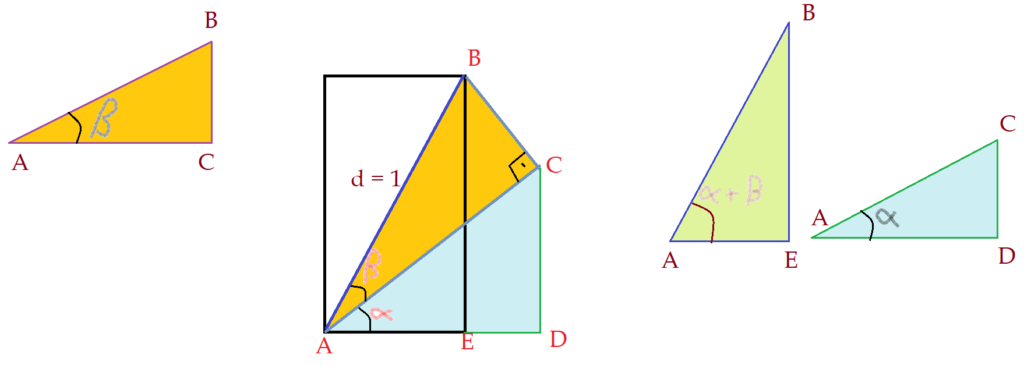
Neste triângulo, veremos:
$sen\beta = {{\overline{BC}}\over\overline{AB}}$
$sen\beta = {{\overline{BC}}\over 1}$$\Leftrightarrow$$sen\beta =\overline{BC}$ (V)
$cos\beta = {{\overline{AC}}\over 1}$$\Leftrightarrow$$cos\beta = \overline{AC}$ (VI)
Falta completar o quarto triângulo. Prolongamos a base superior do retângulo e o segmento $\overline{CD}$, formando $\Delta{CBFC}$, que é semelhante ao triângulo $\Delta{ACDA}$. São semelhantes pois ambos são retângulos e os lados são respectivamente perpendiculares. Por isso o ângulo com vértice no ponto $C$ é congruente ao ângulo $\alpha$.
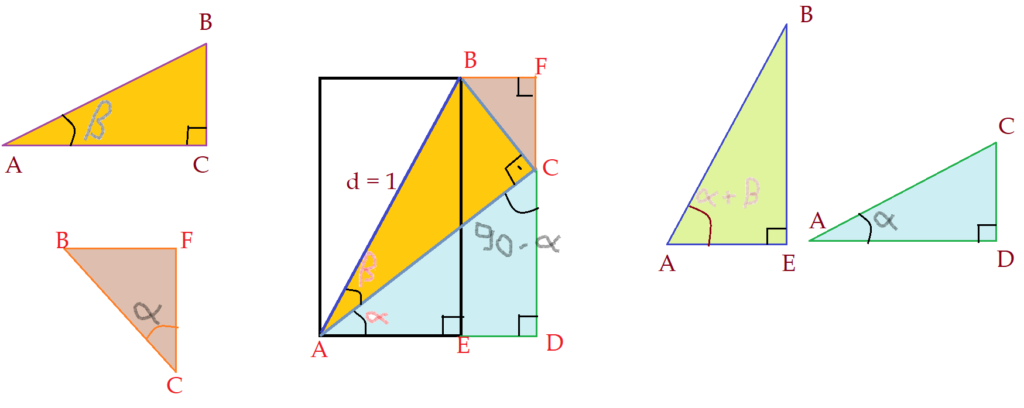
Aqui temos: $sen\alpha = {{\overline{BF}}\over\overline{BC}}$ (VII)
$cos\alpha = {{\overline{CF}}\over\overline{BC}}$ (VIII)
Resumo:
$sen{(\alpha + \beta)} = {{\overline{BE}}\over\overline{AB}}$ (I)
$cos{(\alpha + \beta)} = {{\overline{AE}}\over\overline{AB}}$ (II)
$sen\alpha\cdot\overline{AC} = \overline{CD}$ (III)
$cos\alpha\cdot\overline{AC} = \overline{AE}$ (IV)
$sen\beta =\overline{BC}$ (V)
$cos\beta = \overline{AC}$ (VI)
Substituindo (V) em (VII) e (VIII):
$sen\alpha = {{\overline{BF}}\over sen\beta}$
${sen\alpha\cdot sen\beta} = \overline{BF}$ (IX)
$cos\alpha = {{\overline{CF}}\over sen\beta}$
${cos\alpha\cdot sen\beta} = \overline{CF}$ (X)
Substituindo (VI) em (III) e (IV), fica:
${sen\alpha\cdot\cos\beta} = \overline{CD}$ (XI)
${cos\alpha\cdot\ cos\beta} = \overline{AE}$ (XII)
Na figura principal, observamos que os segmentos:
$\overline{BE} = \overline{CD} + \overline{CF}$
$\overline{AE} = \overline{AD} – \overline{ED}$
Olhando as expressões (I) e (II), podemos deduzir que:
$\overline{BE} = sen{(\alpha + \beta)}$
$\overline{AE} = cos{(\alpha + \beta)}$
De onde podemos tirar que:
$sen{(\alpha + \beta)}= {sen\alpha\cdot cos\beta + sen\beta\cdot cos\alpha}$
$cos{(\alpha + \beta)} = {cos\alpha\cdot cos\beta – sen\alpha\cdot sen\beta}$
Se em lugar de $\alpha + \beta$, tivéssemos $\alpha – \beta$, bastaria trocar os sinais +/- nas expressões, ficando:
$sen{(\alpha \pm \beta)} = {sen\alpha\cdot cos\beta \pm sen\beta\cdot cos\alpha}$
$cos{(\alpha \pm \beta)} = {cos\alpha\cdot cos\beta \mp sen\alpha\cdot cos\beta}$
A partir dessas expressões podemos obter também a tangente e cotangente da soma de ângulos. Vejamos:
$tg{(\alpha + \beta)} = \left[{{sen{(\alpha +\beta)}}\over{cos{(\alpha + \beta)}}}\right]$
$tg{(\alpha + \beta)} = \left[{{sen\alpha\cdot cos\beta + sen\beta\cdot cos\alpha}\over{cos\alpha\cdot cos\beta – sen\alpha\cdot sen\beta}}\right]$
Dividindo todos os termos do segundo membro da equação por $sen\alpha\cdot cos\beta$, teremos:
$tg{(\alpha + \beta)} =\left[{{\left({{sen\alpha\cdot cos\beta}\over{sen\alpha\cdot cos\beta}}\right) + \left({{sen\beta\cdot cos\alpha}\over{sen\alpha\cdot cos\beta}}\right)}\over{\left({{cos\alpha\cdot cos\beta}\over{sen\alpha\cdot cos\beta}}\right) – \left({{sen\alpha\cdot sen\beta}\over{sen\alpha\cdot cos\beta}}\right)}}\right]$
$\color{maroon}{tg{(\alpha + \beta)} = {{1 + tg\beta\cdot ctg\alpha}\over{ctg\alpha – tg\beta}}}$
Sendo $ctg{(\alpha + \beta)} = {1\over tg{(\alpha + \beta)}}$, podemos escrever que:
$\color{maroon}{ctg{(\alpha + \beta)} = {{ctg\alpha – tg\beta}\over{1 + ctg\beta\cdot tg\alpha}}}$
Arco duplo – Seno, cosseno e …
As relações da soma e diferença de ângulos, são úteis na obtenção dos chamados “arcos duplos ou triplos”.
${sen(2\alpha)} = ?$
Lembrando que $2\alpha = \alpha + \alpha$
$sen(2\alpha) = sen\alpha\cdot cos\alpha + sen\alpha\cdot cos\alpha$
$\color{maroon}{sen(2\alpha) = 2\cdot sen\alpha\cdot cos\alpha}$
$cos(2\alpha) = cos\alpha\cdot cos\alpha – sen\alpha\cdot sen\alpha$
$\color{maroon}{cos(2\alpha) = cos^2\alpha – sen^2\alpha}$
$tg(2\alpha) = \left({{2sen\alpha\cdot cos\alpha}\over{cos^2\alpha – sen^2\alpha}}\right)$
$tg(2\alpha) =\left[{\left({{2sen\alpha\cdot cos\alpha}\over{sen\alpha\cdot cos\alpha}}\right)\over\left({{cos²\alpha – sen²\alpha}\over{sen\alpha\cdot cos\alpha}}\right)}\right]$$\Leftrightarrow$$tg(2\alpha) = \left[{2\over{{{cos^2\alpha}\over{sen\alpha\cdot cos\alpha}}} – {{sen^2\alpha}\over{sen\alpha\cdot cos\alpha}}}\right]$
$\color{Maroon}{tg(2\alpha) = {2\over{ctg\alpha – tg\alpha}}}$
Como $ctg(2\alpha) = {1\over{tg(2\alpha)}}$
temos que:
$\color{maroon}{ctg(2\alpha) = {{ctg\alpha – tg\alpha}\over 2}}$
$csc(2\alpha) = {1\over sen(2\alpha)}$
$csc(2\alpha) = {1\over{2sen\alpha\cdot cos\alpha}}$
$\color{maroon}{sec(2\alpha) = {1\over{cos^2\alpha – sen^2\alpha}}}$
Vamos deixar os exercícios para o próximo post, que será bem recheado deles. Se existir alguma dúvida sobre as demonstrações, por obséquio, pergunte para esclarecer. Não há necessidade de decorar esses procedimentos, mas entender de onde vem as expressões que depois serão utilizadas.
Curitiba, 30 de novembro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

