Vamos tornar os radicais mais simples
O que vimos no post anterior, permite fazer algumas transformações que nos ajudam em muitas situações a obter um radical mais simples ou escrito de forma mais conveniente à situação com que nos deparamos.
Tomemos como exemplo o radical.
$\root 6 \of {2000} = ?$
Decompondo o radicando $2000$ em seus fatores primos, teremos:

$\root 6 \of {{2^4}\cdot {5^3}}=?$
Transformando em potências com expoentes fracionários fica:
${2^ \frac{4}{6}}\cdot{5^ \frac{3}{6}} = ?$
Simplificando os expoentes ficamos com:
${2^ \frac{2}{3}}\cdot {5^\frac{1}{2}} =?$
Reescrevendo na forma de radical, fica:
$\root 3\of {2^2}\cdot \sqrt {5} $
Resultou um produto de dois radicais de índices diferentes e expoentes menores.
Vejamos um exemplo diferente:
$\root 3 \of {1728} =?$
Em fatores primos, temos: 
$\root 3 \of{{2^6}\cdot{3^3}} = ?$
Em forma de expoentes fracionários:
${2^\frac{6}{3}}\cdot {3^\frac{3}{3}} =?$
${{2^2}\cdot {3^1} = 4\cdot 3 = 12}$
Neste caso temos um radicando com raiz exata e não há mais necessidade do uso de radical.
Vamos ver outro exemplo:
$\root 5 \of {256} = ?$
Começamos novamente decompondo em fatores primos.
$\root 5 \of {2^6} = \root 5 \of {{2^5}\cdot {2}} $
Obs.: a potência $2^6$ foi desdobrada em multiplicação de potências de mesma base $ {2^5}\cdot {2}$.
${2^\frac{5}{5}}\cdot {2^\frac{1}{5}} = 2\cdot {\root 5 \of2}$
Veja que ficou bem simplificado o radical.
Mais um exemplo:
$\sqrt {216} = ?$
Da decomposição em fatores primos resulta: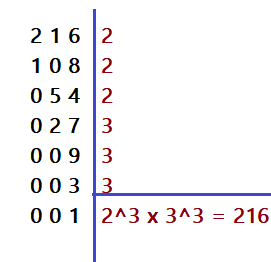
$\sqrt {{2^3}\cdot {3^3}}= ?$
Escrevendo as potências como produtos de potências de mesma base, fica:
$\sqrt{{2^2}\cdot{2}\cdot{3^2}\cdot{3}} =?$
${2\cdot 3}\cdot \sqrt{2\cdot3} = 6\cdot\sqrt{6}$
Novo exemplo: $\root 3\of {10125} =?$ 
$\root 3\of {{3^4}\cdot{5^3}} =?$
$\root 3\of {{3^3}\cdot{3}\cdot{5^3}} = ?$
$ 3\cdot \root 3\of {3}\cdot {5} = 15\cdot\root 3\of{3}$
Último exemplo.
$\root 5\of {23328} = ?$
Decompondo em fatores primos.
$\root 5\of {{2^5}\cdot{3^6}} =?$
$\root 5\of{{2^5}\cdot{3^5}\cdot{3}} = 2\cdot {3}\cdot\root 5\of {3} = 6\cdot\root 5\of {3}$
Aproveite para treinar esse assunto. Simplifique os radicais da listagem abaixo.
I) $\root 3\of {243} =?$
II) $\root 5\of {9216} =?$
III)$\sqrt {6912} =?$
IV)$\root 7\of {1024} =?$
V) $\root 4\of {50000} =?$
VI) $\sqrt {24696} =?$
VII)$\sqrt {18000} =?$
VIII)$\root 3\of {10000} =?$
IX) $\root 5\of {18225} =?$
X) $\sqrt {10648} =?$
Havendo dúvidas, entre em contato para esclarecer e resolver suas dificuldades.
Curitiba, 10 de novembro de 2018
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732

