Mês: novembro 2017

Publicado em

01.025 – Matemática – Aritmética, fração, razão, proporção.

Fração

  • Se você procurar no dicionário o significado da palavra fração, deverá encontrar entre diferentes respostas uma que é relativa ao que pretendo apresentar nesse artigo. Denominamos fração a um número representado pela divisão indicada de dois números quaisquer. Ao primeiro chamamos numerador e  é escrito acima de um traço horizontal ou inclinado para direita. Ao segundo chamamos denominador e é escrito abaixo do mesmo traço. Vejamos os exemplos:
  • \[\bbox[4px,border:2px solid Olive]{\mathbf{\color{Brown}{\frac{3}{4}}}}\]
  • \[\bbox[4px,border:2px solid Olive]{\mathbf{\color{Brown}{\frac{5}{7}}}}\]
  • \[\bbox[4px,border:2px solid Olive]{\mathbf{\color{Brown}{\frac {12}{9}}}}\]

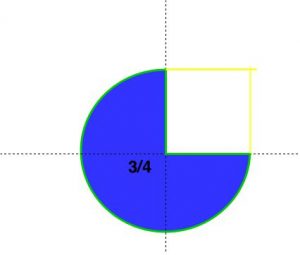
No primeiro exemplo temos como numerador $\color{navy}{3}$ e denominador $\color{navy}{4}$. O numerador indica quantas partes do inteiro foram tomadas e o denominador, indica em quantas partes o inteiro foi dividido. Podemos representar isso graficamente assim:

Treinamento de força em casa – 5 programas, 9 exercícios vardenafil 20mg rack de musculação de tração de agachamento domyos decathlon.
Fração 3-4 de um círculo
Fração três quartos de um inteiro.

Note que o circulo foi dividido em quatro partes iguais. Destas foi removida uma parte, restando três. Essa figura representa a fração

  • $\mathbf{\color{Navy}{3/4}}$ ou $\mathbf{\color{Navy}{\frac {3}{4}}}$

A parte que foi removida corresponde ao que falta para o inteiro e é representada pela fração

  • $\mathbf{\color{Navy}{1\over 4}}$

Obs.: Repare no detalhe do numerador, partes tomadas e do denominador, partes em que foi dividido o inteiro.

Continue lendo “01.025 – Matemática – Aritmética, fração, razão, proporção.”
Publicado em

01.024 – Matemática – Aritmética. Potências com expoente negativo.

Radiciação, Potênciação, expoente negativo.

Já vimos que a radiciação é a operação inversa da potênciação. Lembrando:

  • Expoente igual a zero : potência de expoente zero, tem valor igual a 1.
  •  divisão de potências de mesma base: conserva a base e subtrai os expoentes. 
  • Então vejamos o seguinte:   \[\bbox[4px,border:2px solid Olive]{\color{Navy}{\frac {1}{3^5}}}\]

Como vimos acima, podemos substituir o número 1, por uma potência de qualquer base e expoente igual a 0(zero). Assim nossa expressão acima, irá ficar:

\[\bbox[4px,border:2px solid Olive]{\color{Navy}{\frac {3^0}{3^5}  = 3^{(0 – 5)}}}\]

Não resta dúvida de que a expressão \[\bbox[4px,border:2px solid Olive]{\color{Navy}{\frac{1}{3^5} = 3^{-5}}}\]

  • Podemos converter denominador com determinado expoente,em um fator acima do traço de fração, ou seja parte do numerador, trocando sinal do expoente. Mais exemplos:
  • $\color{Brown}{\frac {1}{5^3} = 5^{-3}}$
  • $\color{Brown}{\frac{1}{2^4} = 2^{-4}}$
  • $\color{Brown}{\frac{2}{3^{-2}} = 2\times {3^2}}$
  • $\color{Brown}{\frac{3^5}{5^{-4}} = {3^5}\times{5^4}}$

Não fica difícil entender que, o denominador com expoente negativo, passa para o numerador com o mesmo expoente, porém positivo. Vejam como:

  • $\color{Maroon}{\frac {1}{7^{-5}}  = 7^5 }$
  • $\color{Maroon}{\frac{1}{{11}^{-4}} = {11}^4}$

Do mesmo modo, podemos transformar uma potência com expoente negativo, em fração cujo numerador é a unidade e o denominador a mesma potência com expoente positivo. Assim:

  • $\color{Maroon}{7^{-3} = \frac{1}{7^3}}$
  • $\color{Maroon}{5^{-7} = \frac{1}{5^7}}$

Continue lendo “01.024 – Matemática – Aritmética. Potências com expoente negativo.”

Publicado em

01.023 – Matemática – Aritmética. Potenciação de números relativos

Potências de números relativos.

Para começar o assunto, vamos lembrar que potenciação é uma multiplicação de fatores iguais. Portanto iremos fazer uso do assunto visto no post anterior sobre a multiplicação. Vamos aos exemplos.

$$\begin{align}{(+ 3)^3}& = {(+3)\times (+3)\times (+3)}& ={+ 27}\end{align}$$

$$\begin{align}{(+ 2)^2} &= {(+2)\times(+2)}& = {+ 4}\end{align}$$

$$\begin{align}{(- 5)^2}&={(- 5)\cdot(- 5)}& = { + 25}\end{align}$$

$$\begin{align}{(-4)^3}&= {(- 4)\times(- 4)\times(- 4)}&= {- 64}\end{align}$$

$$\begin{align}{(- 2)^4}& ={(-2)\times(-2)\times(-2)\times(-2)}&= {+16}\end{align}$$

$$\begin{align}{(-3)^5}&={(-3)\times(-3)\times(-3)\times(-3)\times(-3)}&= {-243}\end{align}$$

Continue lendo “01.023 – Matemática – Aritmética. Potenciação de números relativos”

Publicado em

01.022 – Matemática – Aritmética. Multiplicação e divisão de números relativos

Multiplicação de relativos.

  • Números positivos.

    Vamos multiplicar os números:

  • $\bbox[4px,border:2px solid Olive]{\color{Brown}{(+5)\times (+3)}}$
    • $\color{Navy}{(+5)\times (+3) = (+5) + (+5) + (+ 5) = 15}$
  • $\bbox[4px,border:2px solid Olive]{\color{Brown}{(+4)\times(+2)}}$
    • $\color{Navy}{(+4 )\times (+2)= (+4) + (+4)= 8}$
  • Para multiplicar números positivos multiplicamos os módulos e ao resultado damos o sinal (+). 

Obs.: Temos que lembrar de uma coisa. A multiplicação é uma soma de parcelas iguais. Temos o multiplicando e o multiplicador, isto é, o número que está sendo multiplicado e o que está multiplicando. Nada impede a inversão dessas posições, de acordo com a propriedade comutativa. Isso transforma a multiplicação em uma soma de tantas parcelas (multiplicando), iguais a quantidade expressa pelo multiplicador.

  • Números negativos.

  • Sejam os números:

    $\bbox[4px,border:2px solid Olive]{\color{Brown}{(- 4)\times (- 5)}}$

    $\bbox[4px,border:2px solid Olive]{\color{Brown}{(- 7)\times (- 4)}}$

    • $\color{Navy}{(-4)\times (-5) = {- (-4) – (-4) – (-4) – (-4) – (-4) = 4 + 4 + 4 + 4 + 4}= 20}$
    • $\color{Navy}{(- 7)\times (-4) = – (-7) – (-7) – (-7) – (-7) =  7 + 7 + 7 + 7 = 28}$
  • Ao multiplicar dois números negativos, multiplicamos os módulos e atribuímos o sinal (+).
  •  Resumindo podemos dizer que na multiplicação de números de sinais iguais, o resultado é positivo. 

  • Números de sinais contrários.

Sejam os números:

  • $\bbox[4px,border:2px solid Olive]{\color{Brown}{(- 6)\times (+ 3)}}$
  • $\bbox[4px,border:2px solid Olive]{\color{Brown}{(+ 7)\times (-4)}}$
  • $\color{Navy}{(- 6)\times (+3) = +(-6) + (-6) + (-6) = -6 -6 -6 = -18}$
  • $\color{Navy}{(+ 7)\times (-4) = -( +7) – (+7) – (+ 7) – (+7) = – 7 – 7 – 7 – 7 = – 28}$
  • A multiplicação de números de sinais contrários é igual ao produto dos módulos, com o sinal (-), sem importar a ordem dos fatores. 

Resumindo

  • $\bbox[4px,border:2px solid Olive]{\color{Brown}{(+)\times (+) = \{+\}}}$
  • $\bbox[4px,border:2px solid Olive]{\color{Brown}{(-)\times (-) = \{+\}}}$
  • $\bbox[4px,border:2px solid Olive]{\color{Brown}{(+)\times (-) = \{-\}}}$
  • $\bbox[4px,border:2px solid Olive]{\color{Brown}{(-)\times (+) = \{-\}}}$

Continue lendo “01.022 – Matemática – Aritmética. Multiplicação e divisão de números relativos”

Publicado em

01.021 – Matemática, aritimética. Adição e subtração de números relativos.

Operações com números relativos – adição.

  • Números com o mesmo sinal e sinais opostos.

Vamos usar exemplos práticos. Você e seu irmão trabalham, recebendo por dia de serviço. Se seu trabalho rende $\color{Navy}{R\$ 100,00}$ por dia e o de seu irmão $\color{Navy}{R\$ 110,00}$ por dia. Quanto terão a receber ao final de um dia de serviço?

É fácil dizer que a soma será de $\color{Brown}{100,00 + 110,00 = 210,00}$. Representando os valores ganhos como números positivos, podemos escrever:

$$\color{Maroon}{(+100) + (+110,00)= + 210,00}$$

Vamos supor que vocês compraram uma muda de roupas para cada um, gastando $\color{Navy}{R\$ 90,00}$ na sua roupa e $\color{Navy}{R\$ 85,00}$ na roupa do seu irmão. O dinheiro gasto, podemos representar por valores negativos, pois irão diminuir o saldo disponível.

  • $$\color{Navy}{(- 90,00) + (- 85,00) = -175,00}$$

Vamos determinar o saldo que sobra no seu bolso e no de seu irmão.

  • $$\color{Navy}{(+100,00) + (- 90,00)= +10,00}$$

No seu bolso haverá o saldo de $\color{Brown}{R$ 10,00}$.

  • $$\color{Navy}{(+ 110,00) +(- 85,00)= +25,00}$$

No bolso de seu irmão, haverá um saldo de $\color{Brown}{R$ 25,00}$.

Continue lendo “01.021 – Matemática, aritimética. Adição e subtração de números relativos.”

Publicado em

01.020 – Matemática, aritmética. Números inteiros relativos.

Números relativos.

Nos primórdios da matemática, surgiram primeiramente os números, hoje denominados Números Naturais, associados a quantidades de objetos. A necessidade de exprimir quantidades que não representam um número inteiro de objetos, fez surgir as divisões decimais. Os algarismos após a vírgula, mas exatos, ou as dízimas periódicas. Isso ampliou grandemente as opções de resolução de problemas. Persistia no entanto um problema. A subtração só era possível se o minuendo tivesse valor maior que o subtraendo. Isso deixava a operação de subtração impossível em muitas situações. Como a necessidade costuma resultar no surgimento de inovações, foi também aqui que surgiu o que hoje conhecemos como Conjunto de Números Inteiros Relativos e posteriormente, os Racionais Relativos. 

Continue lendo “01.020 – Matemática, aritmética. Números inteiros relativos.”

Publicado em

01.019 – Matemática – Aritmética, Teoria dos conjuntos. Diferença entre conjuntos

Diferença entre conjuntos.

Em artigos anteriores falamos de intersecção, reunião ou união, conjuntos disjuntos. Faltou apenas uma coisa. Diferença entre dois conjuntos A e B.

  • Denominamos diferença entre os conjuntos$\color{Navy}{A}$ e $\color{NavyBlue}{B}$, ao conjunto dos elementos pertencentes ao conjunto $\color{NavyBlue}{A}$ , que não pertencem ao conjunto $\color{NavyBlue}{B}$ . Um Diagrama de Venn pode nos mostrar graficamente como é.
  • $\color{Brown}{A = \{m, n, o, p, q\}}$
  • $\color{Brown}{B =\{p, q, r, s, t\}}$
  • $\color{OliveGreen}{A – B = \{m, n, o\}}$ ou $\color{OliveGreen}{A/B = \{m, n, o\}}$
  • $\color{OliveGreen}{B – A = \{r, s, t\}}$ ou  $\color{OliveGreen}{B/A = \{r, s, t\}}$

Continue lendo “01.019 – Matemática – Aritmética, Teoria dos conjuntos. Diferença entre conjuntos”

Publicado em

01.018 – Matemática, Teoria dos conjuntos. Intersecção e união de conjuntos.

Operações com conjuntos.

  • União ou reunião de conjuntos.

Sejam:

  • $\color{Navy}{A = \{a,e,i,o,u\}}$ $\rightarrow$ conjunto das vogais.
  • $\color{Navy}{B = \{a,b,c,d,e,…,x,y,z\}}$$\rightarrow$ alfabeto latino.

A união ou reunião desses dois conjuntos, formará o conjunto das letras do alfabeto. Simbolicamente representamos isso da seguinte maneira:

  • $\color{Navy}{A \cup B = U =\{a,b,c,d,e,f,g,…,x,y,z\}}$
  • Vemos que ao unir um conjunto a um de seus sub-conjuntos, o resultado é o próprio conjunto.

Num Diagrama de Venn:

Rendered by QuickLaTeX.com

Continue lendo “01.018 – Matemática, Teoria dos conjuntos. Intersecção e união de conjuntos.”

Publicado em

01.017 – Matemática, Teoria dos conjuntos. Relação de pertinência, sub-conjuntos.

Relação de pertinência.

Pertence/não pertence

Para dizer que um determinado elemento faz parte ou não de um conjunto, usamos as palavras pertence  e não pertence. Simbolicamente, usamos $\in$ e $\notin$. 

Assim, dado o conjunto das vogais:

$V = {a, e, i, o, u}$ podemos dizer que:

  • $a\in V$$\Rightarrow$ “a pertence ao conjunto V”;
  • $i\in V$$\Rightarrow$ “ i pertence ao conjunto V“;
  • $u\in V$$\Rightarrow$”u pertence ao conjunto V”;
  • $m\notin V$$\Rightarrow$ “m não pertence ao conjunto V”;
  • $r\notin V$$\Rightarrow$ “r não pertence ao conjunto V”;

e assim sucessivamente.

Subconjunto

Tomemos por exemplo o conjunto das vogais.

  • $\bbox[4px,border:2px solid Olive]{\color{Navy}{ A = \{a, e, i, o, u\}}} $

Denominamos sub-conjunto  de um conjunto dado, a todo conjunto cujos elementos pertençam a este conjunto. No exemplo acima, conjunto das vogais, temos 5 (cinco) elementos. Vimos que existe o conjunto vazio, que não tem nenhum elemento; conjunto unitário com um elemento apenas e assim por diante. Iremos formar um conjunto de subconjuntos do conjunto $\color{Navy}{A}$, também denominado conjunto das partes. Vejamos detalhadamente.

Continue lendo “01.017 – Matemática, Teoria dos conjuntos. Relação de pertinência, sub-conjuntos.”

Publicado em

01.016 – Matemática – Teoria dos Conjuntos

Matemática – teoria dos conjuntos.

  • O que é um conjunto?

Creio que não haverá dificuldades em entender o que é um conjunto. Na sua casa, deve haver vários conjuntos. Por exemplo: um conjunto de pratos, um conjunto de copos, um conjunto de xícaras, um conjunto de cadeiras, um conjunto de móveis, um ou vários conjuntos de brinquedos, seus e seus irmãos ou irmãs. Poderíamos citar mais uma porção de outros.

O que fica claro é que são coisas ou objetos que fazem parte de um grupo. Podemos estender esse conceito um pouco mais e teremos o que em matemática se chama conjunto. Podemos ter um conjunto de símbolos, letras, estrela, círculos, números e assim por diante. Da mesma forma como nossos pais quando nascemos, nos batizaram e fizeram nosso registro de nascimento identificando-nos por um nome, os nossos conjuntos em matemática, receberão um nome. Melhor dizendo, serão identificados por uma letra maiúscula: A, B, C, D, etc. Sempre que nos referirmos a um conjunto usaremos uma letra para identificar esse conjunto.

Continue lendo “01.016 – Matemática – Teoria dos Conjuntos”