Fração
- Se você procurar no dicionário o significado da palavra fração, deverá encontrar entre diferentes respostas uma que é relativa ao que pretendo apresentar nesse artigo. Denominamos fração a um número representado pela divisão indicada de dois números quaisquer. Ao primeiro chamamos numerador e é escrito acima de um traço horizontal ou inclinado para direita. Ao segundo chamamos denominador e é escrito abaixo do mesmo traço. Vejamos os exemplos:
- \[\bbox[4px,border:2px solid Olive]{\mathbf{\color{Brown}{\frac{3}{4}}}}\]
- \[\bbox[4px,border:2px solid Olive]{\mathbf{\color{Brown}{\frac{5}{7}}}}\]
- \[\bbox[4px,border:2px solid Olive]{\mathbf{\color{Brown}{\frac {12}{9}}}}\]
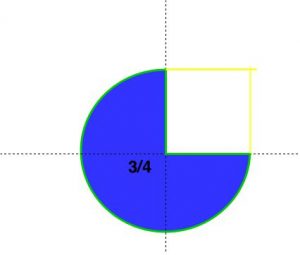
No primeiro exemplo temos como numerador $\color{navy}{3}$ e denominador $\color{navy}{4}$. O numerador indica quantas partes do inteiro foram tomadas e o denominador, indica em quantas partes o inteiro foi dividido. Podemos representar isso graficamente assim:
Treinamento de força em casa – 5 programas, 9 exercícios vardenafil 20mg rack de musculação de tração de agachamento domyos decathlon.Note que o circulo foi dividido em quatro partes iguais. Destas foi removida uma parte, restando três. Essa figura representa a fração
- $\mathbf{\color{Navy}{3/4}}$ ou $\mathbf{\color{Navy}{\frac {3}{4}}}$
A parte que foi removida corresponde ao que falta para o inteiro e é representada pela fração
- $\mathbf{\color{Navy}{1\over 4}}$
Obs.: Repare no detalhe do numerador, partes tomadas e do denominador, partes em que foi dividido o inteiro.
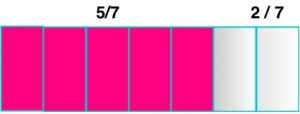
O nosso segundo exemplo
- $\bbox[4px,border:2px solid olive]{\color{brown}{{5}\over{7}}}$
Note agora que um grande retângulo foi dividido em sete partes iguais. Nossa fração é representada pelos retângulos coloridos, em número de $\color{Navy}{5}$, numerador e o total de partes do inteiro é $\color{Navy}{7}$, denominador.
Estes dois exemplos de frações, em que temos o numerador menor que o denominador, recebem o nome de frações próprias, por representar menos do que uma unidade inteira.
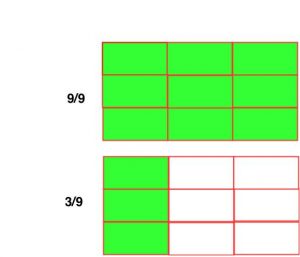
Vejamos o outro exemplo da fração
- $\bbox[4px,border:2px solid Olive]{\mathbf{\color{Brown}{{12}\over{9}}}} $
Temos agora dois retângulos divididos em 9 (nove) partes cada. No primeiro foram coloridas todas as partes, dando a fração
- $\mathbf{\color{Navy}{{9}\over{9}}}$
No segundo foram coloridas apenas três partes que nos dá a fração
- $\mathbf{\color{Navy}{3}\over{9}}$
Se contarmos as partes coloridas, encontraremos $ 9 + 3 = 12 $, que nos dará como resposta 12 partes. Isso resulta na fração
- $\mathbf{\color{Navy}{{12}\over{9}}}$
Já as partes deixadas em branco, são em número de $\color{Navy}{6}$, o que nos permite escrever a fração $\color{Navy}{{6}\over{9}}$
Esse terceiro exemplo é uma fração denominada fração imprópria, por representar mais do que uma unidade inteira. Podemos classificar pois as frações em:
- Próprias, são aquelas em que o numerador é menor que o denominador.
- Impróprias, são aquelas em que o numerador é maior que o denominador.
Uma conclusão fica óbvia diante dessa definição. Toda fração imprópria é maior que qualquer fração própria, pelo fato de a primeira representar mais do que uma unidade e a outra menos que uma unidade.
-
Qual é a fração maior?
Há duas maneiras de comparar frações. Uma é observar os denominadores. Se eles forem iguais, a maior será aquela que tiver o numerador maior. Sejam os exemplos
- $\bbox[5px,border:2px solid Olive]{\mathbf{\color{Brown}{{3}\over{7}}}}$
- $\bbox[5px,border:2px solid Olive]{\mathbf{\color{Brown}{{2}\over{7}}}}$
- $\bbox[5px,border:2px solid Olive]{\mathbf{\color{Brown}{{5}\over{7}}}}$
Observando os denominadores são todos iguais a 7, portanto o inteiro foi dividido em sete partes iguais. Os numeradores são 3, 2 e 5. Se quisermos escrevê-las em ordem crescente, começaremos pelo menor numerador e terminaremos pelo maior: 2, 3 e 5. Fica então:
- $\mathbf{{{2}\over{7}} \lt {{3}\over{7}} \lt {{5}\over{7}}}$
Em ordem decrescente, começamos pelo maior numerador e terminamos pelo menor 5, 3 e 2.
- $\mathbf{{{5}\over{7}} \gt {{3}\over{7}} \gt {{2}\over{7}}}$
Uma outra forma de colocar em ordem crescente ou decrescente as frações, podemos observar se os numeradores são iguais. Nesse caso a maior será aquela que tiver o menor denominador. Vejamos os exemplos das frações:
- $\mathbf{\color{Navy}{{{5}\over{3}},{{5}\over{7}},{{5}\over{9}},{{5}\over{6}}}}$
Veja que os numeradores são todos iguais a 5(cinco). Os denominadores são 3, 7, 9 e 6. Entre eles o menor é o número 3. Na ordem crescente os numeradores ficarão em ordem decrescente: 9, 7, 6, 3. Ficará então:
- $\mathbf{{5\over 9} \lt {5\over7}\lt {5\over6}\lt {5\over3}}$
Na ordem decrescente tomamos os denominadores na ordem crescente: 3, 6, 7, 9.
- $\mathbf{ 5/3 \gt 5/6 \gt 5/7 \gt 5/9} $
-
E se tanto os numeradores quanto os denominadores forem diferentes?
Lembram-se de uma coisa vista anteriormente e que parecia não fazer sentido naquele momento? Estudamos o máximo divisor comum (m.d.c.) e o mínimo múltiplo comum(m.m.c.). Este último é a solução que vem em nosso socorro nesse momento. Para comparar frações de numeradores e denominadores diferentes, vamos fazer o que se denomina redução ao mesmo denominador. Para isso precisamos determinar o m.m.c. dos denominadores, que irá ser o denominador de todas as frações.
Sejam os exemplos: $\mathbf{\frac{3}{2}, \frac {4}{7}, \frac{5}{6}}$
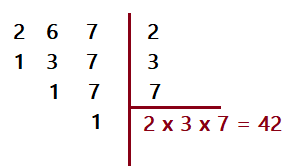
Os nossos denominadores são 2, 6 e 7. Nesse caso 6 é divisível por dois e 6 e 7 são denominados primos entre si, por não terem divisor comum além da unidade. Nosso denominador comum (m.m.c.) será o produto entre 6 e 7. Também podemos colocar os números em linha, dividindo sucessivamente pelos fatores primos comuns, até que todos estejam com quociente 1. O produto dos fatores primos será o m.m.c.
- .$\bbox[5px,border:2px solid Olive]{\mathbf{\color{Navy}{m.m.c. = 2\times 3\times 7 = 42}}}$
Agora nos resta descobrir quais serão os novos numeradores. Isso se faz dividindo o m.m.c. por cada um dos denominadores e multiplicando pelo respectivo numerador. Assim:
- $\mathbf{\color{Navy}{{42}\div 2 = 21}}$ $\mathbf{\Leftrightarrow}$ $\mathbf{\color{Navy}{3\times{21} = 63}}$
Assim podemos escrever $\mathbf{\color{Navy}{{3\over2} = {{63}\over {42}}}}$
- $\mathbf{\color{Navy}{{{42}\div 6} = 7 }}$ $\mathbf{\Leftrightarrow}$ $\mathbf{\color{Navy}{{5\times 7} = 35}}$
Podemos escrever então: $\mathbf{\color{Navy}{{{5\over 6}} = {{35}\over {42}}}}$
Na terceira fração:
- $\mathbf{\color{Navy}{{42} \div 7 = 6}}$ $\mathbf{\Leftrightarrow}$ $\mathbf{\color{Navy}{4\times 6 =24}}$
Podemos escrever: $\mathbf{\color{Navy}{{4\over 7} = {{24}\over{42}}}}$
Se observamos os novos numeradores, veremos que o maior corresponde à 3/2, depois vem 5/6 e por último 4/7. Dessa forma podemos escrever na ordem crescente:
- $\mathbf{\frac {24}{42} \lt \frac {35}{42} \lt\frac{63}{42}} $
- $\mathbf{\frac{4}{7} \lt\frac{5}{6}\lt\frac{3}{2}} $
Na ordem decrescente, teremos:
- $\mathbf{\frac{63}{42} \gt \frac{35}{42}\gt\frac{24}{42}} $
- $\mathbf{\frac{3}{2} \gt\frac{5}{6}\gt\frac {4}{7}} $
- Hora de exercitar o que aprendemos.
- Classificar as frações em próprias ou impróprias.
- $ 3/9 $, $ 7/4 $, $ 4/5 $, $ 6/11 $, $ 8/12 $, $ 15/7 $, $ 9/5 $, $ 10/17$
- Coloque em ordem crescente as frações.
- $ 3/9, 5/9, 4/9, 2/9$
- $ 10/7, 4/7, 2/7, 9/7, 6/7 $
- $ 9/4, 9/7, 9/10, 9/5 $
- $ 10/2, 10/7, 10/4$
- $ 4/3, 5/7, 3/4 e 2/6 $
- $ 5/2, 3/5, 4/3 $
Obs.: Havendo dúvidas na resolução dos exercícios, no entendimento dos conteúdos, faça contato por meio de um dos canais abaixo informados. Estou à disposição para assuntos de matemática e física, ainda não abordados em nenhuma postagem.
Curitiba, 26 de março de 2015 (Atualizado e revisado neste dia 18/07/2016)
Décio Adams
-
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
- Classificar as frações em próprias ou impróprias.
- Hora de exercitar o que aprendemos.