Inequação! Que é isso?
Lembremos que uma equação é uma igualdade, entre duas quantidades, representadas por números, letras e expressões de letras com números. O prefixo in é uma negação. Assim a palavra inequação, poderíamos dizer, que é a negação de uma equação. Em outras palavras é uma desigualdade. Existem alguns símbolos que usamos para indicar essas desigualdades como:
- “Menor do que” $\Rightarrow\color{maroon}{ \mathbf{\lt}} $
- “maior do que” $\Rightarrow \color{maroon}{\mathbf{\gt}} $
- “menor ou igual a” $\Rightarrow \color{maroon}{\mathbf{\le}} $
- “maior ou igual a” $\Rightarrow\color{maroon}{\mathbf{ \ge}} $
- “Diferente” $\Rightarrow\color{maroon}{\mathbf{\neq}} $
- “Não menor do que” $\Rightarrow\color{maroon}{\mathbf{\not\lt}} $
- “Não maior do que” $\Rightarrow\color{maroon}{\mathbf{\not\gt}} $
- “Não menor ou igual a” $\Rightarrow\color{maroon}{\mathbf{\not\le}}$
- “Não maior ou igual a” $\Rightarrow\color{maroon}{ \mathbf{\not\ge}}$
Em determinados momentos, todos esses símbolos podem aparecer em uma expressão matemática. No caso presente, estudo das inequações, iremos usar principalmente os quatro primeiros. Vejamos alguns exemplos:
- $\bbox[5px,border:2px solid brown]{\color{navy}{2x -3 \lt 0}} $
- $\bbox[5px,border:2px solid brown]{\color{navy}{ x + 7 \gt 2}} $
- $\bbox[5px,border:2px solid brown]{\color{navy}{ 8 -x \ge 5}}$
- $\bbox[5px,border:2px solid brown]{\color{navy}{ 4 + x \le 2x}} $
- A determinação do conjunto verdade de uma inequação, é feita de modo semelhante ao procedimento adotado nas equações, com algumas peculiaridades próprias.
- Vamos pegar como exemplo a primeira das quatro citadas acima:
- $\bbox[5px,border:2px solid brown]{\color{navy}{2x – 3\lt 0}}$.
- O objetivo é obter uma desigualdade que indique onde estão localizados os valores que servem para substituir x nessa inequação. Temos então que deixar o x isolado no primeiro membro.
- \[ 2x – 3 + 3 \lt 0 + 3 \] \[2x \lt 3 \] \[ {{2x}\over 2} \lt {3\over 2} \] \[ x \lt {3\over 2} \]
- Isso nos mostra que todos os números reais, menores do que o número 3/2 servem para x, isto é, transformam a expressão em uma sentença verdadeira. Logo: \[\bbox[5px,border:2px solid brown]{\color{navy}{ V =\left\{ x\in R | {x\lt {3\over 2}}\right\}}} \]
- Representando o conjunto dos números reais na Reta Real, o conjunto verdade dessa inequação será formado por todos os números associados aos pontos dessa reta, à esquerda do ponto que corresponde ao número 3/2.
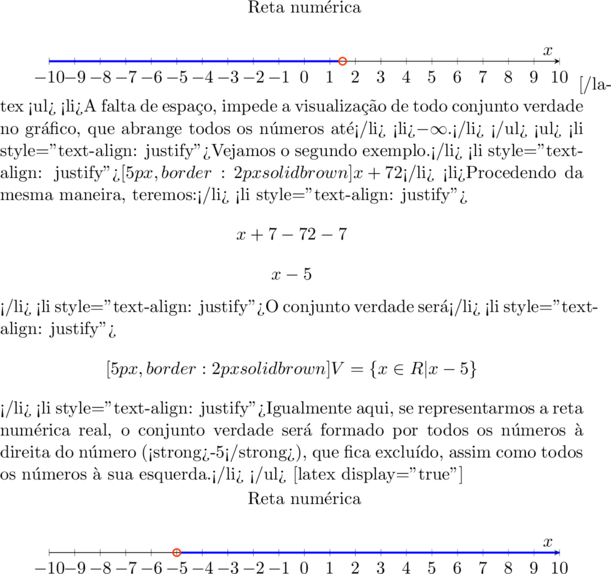
- A vez da terceira:
- $\bbox[5px,border:2px solid brown]{\color{navy}{ 8 -x \ge 5}} $
- Aplicando o mesmo procedimento, ficamos com:
- \[ 8 – 8 – x \ge 5 – 8 \] \[ -x \ge -3 \]
- Observe que o os dois membros da inequação são precedidos do sinal $-$, o que nos indica que para melhor interpretação, devemos multiplicar a expressão toda $-1$. Lembrando da reta numérica, vamos observar que a posição dos números negativos, fica invertida em relação ao zero$(0)$, isto é, quanto maior for o módulo, mais à esquerda ele se situa. A consequência disso é que, a multiplicação de uma inequação por $-1$, inverte o sentido da desigualdade, ou seja se era $\le$, passa para $\ge$ e vice-versa. Vamos ver como fica nosso exemplo.
- \[ {(-x \ge – 3)}\cdot{(-1)} \] \[ x\le 3 \]
- O conjunto verdade dessa inequação será pois:
- \[\bbox[5px,border:2px solid brown]{\color{navy}{ V = \{x\in R|{x\le 3}\}}} \]
- Neste caso o número $3$, faz parte do conjunto verdade. Ficam excluídos apenas os números à direita do $3$. Na Reta Real fica:

- O último exemplo:
- $\bbox[5px,border:2px solid brown]{\color{navy}{ 4 + x \le 2x}} $
- Aplicando o raciocínio par isolar a variável, temos:
- \[ 4 – 4 + x \le 2x – 4 \] \[ x – 2x \le 2x – 2x – 4 \] \[ -x \le -4 \]
- Novamente é preciso multiplicar por $-1$, e inverter o sinal da desigualdade.
- \[{(-x \le -4)}\cdot{(-1)} \] \[ x \ge 4 \]
- O conjunto verdade será composto por todos os números reais, desde o $4$ inclusive, até infinito$\infty$.
- \[\bbox[5px,border:2px solid brown]{\color{navy}{V = \{x\in R|{x\ge 4}\}}} \]
- Na Reta Real, teremos:

- O final da resolução de qualquer inequação de primeiro grau será sempre a variável, seguida de um sinal de desigualdade e depois um número. Se a variável tiver sinal negativo, devemos multiplicar por $\color{Brown}{-1}$ e inverter o sinal da desigualdade. Isso não pode ser esquecido.
Vamos “malhar”?
- Determine o conjunto verdade das inequações a seguir.
- $\color{navy}{ 4x – 7 \lt 2x + 1}$
- $\color{navy}{ 11 + 3x \gt – 8} $
- $\color{navy}{ – 6 + 2x \ge 3x + 1}$
- $\color{navy}{ 6 \le 5 – 3x} $
- $\color{navy}{ 3y + 4 \le 7 – y} $
- $\color{navy}{15 – 4x \lt 11 +x}$
- $\color{navy}{ 6x + 5\gt 4x – 7}$
- $\color{navy}{ 2 + 7x \ge 6x + 4} $
Curitiba, 21 de maio de 2016.
Curitiba, 07 de janeiro de 2018 (Revisto e republicado)
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@adamsDcio
Fone: (41) 3019-4760
Celular: (41) 99805-0732

