Logaritmos
Comecemos pela etimologia da palavra. Tal como uma grande quantidade de termos hoje empregados, também esse tem sua origem na língua grega.
“Logos” ⇒ razão
“Arithmos” ⇒ número
Juntando as duas partes, formamos facilmente a palavra “logaritmo”, significando “número de razão”.
Primeiros indícios
Existem vestígios em escritos da era babilônica, permitindo identificar sinais da utilização de tabelas logarítmicas entre eles. Mais tarde Arquimedes, ao se deparar com números muito grandes, também faz tentativas de estabelecer alguma coisa nesse sentido. Nos séculos XV, XVI e XVII, ocorreu uma intensificação das navegações marítimas; comércio entre pontos distantes do planeta cresceu muito. Como consequência surgiu a necessidade de executar cálculos cada vez mais complexos e por vezes tediosos. Isso foi devido a necessidade de traçar rotas, desenhar mapas, assim como computar os lucros e as despesas das operações comerciais. As operações de multiplicação e divisão, com números cada vez maiores, sem auxílio de recursos mecânicos, muito menos eletrônicos, tornava a tarefa hercúlea.
Os cálculos geográficos utilizavam-se das tabelas de relações trigonométricas. Mesmo assim havia abundância de multiplicações, divisões e potenciações a realizar, por vezes em períodos de tempo exíguos dadas as circunstâncias.
John Neper ou (Napier)
Nascido em 1550, John Neper ou simplesmente Napier, era possuidor de diversas propriedades na Escócia. Nos intervalos entre as atividades de administrar seus bens, dedicava-se a escrever sobre assuntos variados, sendo um deles as sequências de potências sucessivas. Cerca de 50 anos antes (+/- 1544), Stiefel havia publicado o que observara a respeito. Pesquisou e constatou indícios de coisa semelhante nos tratados de Arquimedes.
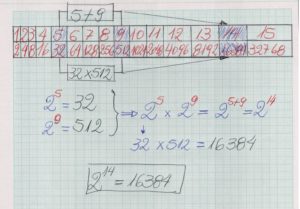
Quando estudamos as operações com potências, vemos que a multiplicação entre duas potências de mesma base, é resolvida, mantendo-se a base e elevando-a a um expoente igual a soma dos expoentes.
Na linha de cima temos os números naturais diferentes de zero e que servem de expoentes. Na linha de baixo, estão os valores das potências do número dois, elevados aos expoentes da linha de cima.
Se temos $ {a^m}\cdot{a^n}$
a resolução é feita por essa maneira
${a^{(m + n)}}$
Então ${a^m}\cdot{a^n} = {a^{(m + n)}}$
Napier imaginou que, se existisse uma tabela semelhante a essa, com intervalos menores entre os produtos(potências), seria possível usá-la para obter os resultados de muitas multiplicações, apenas consultando a tabela. Para diminuir os intervalos, ele fez sucessivas tentativas e chegou ao que hoje é tido como base dos logaritmos naturais ou neperianos. Chegou ao que procurava, usando a razão ${1 – [1/(10^7)]}$, cujo resultado é aproximadamente 0,9999999. Na tabela mostrada na figura acima, a razão é 2 e ele buscava algo próximo de 1.
Para eliminar os algarismos decimais sucessivos, ele adotou multiplicar as potências obtidas por ${10^7}$. Com isso chegou a uma tabela, que tinha na primeira linha os números L e na segunda linha os números N, o que lhe deu a expressão
${N = 10^7\{1 – [1/(10^7)]\}^L}$
O expoente L recebeu o nome de logaritmo de N . Se eventualmente $L = 0$, resultará ${N = 10^7}$. Nesta tabela o logaritmo de ${10^7}$ fica sendo igual a 1. Devemos lembrar que toda potência cujo expoente é 0 (zero), tem valor 1, conforme foi estudado na potenciação.
Em 1514 John Neper publicou suas descobertas sob o título Mirifici logatithmorum canonis descriptio (Descrição do maravilhoso método dos logaritmos).
Na mesma época o suiço Joost Burgi (1552/1632), apresentou uma proposta idêntica, apenas usando a razão 1,0001 e o primeiro termo igual a ${10^8}$, tendo criado uma tabela de 20000 termos. Mas foi o matemático inglês Henry Briggs (1561/1630) que, ao tomar conhecimento do trabalho publicado por Napier, foi ao seu encontro para lhe externar as congratulações.
Briggs sugeriu à Napier adotar uma base decimal, dando assim origem aos logaritmos decimais ou comuns como são usados largamente nos dias atuais. De comum acordo eles estabeleceram que o logaritmo de 1 seria 0 (zero).
${log_{10} {1} = 0}$
Além disso o logaritmo de 10 seria igual a 1 (um)
${log_{10}{10} = 1}$
Teve início uma atividade intensa para elaborar as denominadas tábuas de logaritmos, que permitiam resolver uma imensa quantidade de operações matemáticas. Beneficiaram-se com isso os navegadores, os guarda livros dos comerciantes, bem como os astrônomos como Tycho Brahe, Johannes Kepler, Copérnico, Galileu Galilei e outros que lhes sucederam.
Em pouco tempo os logaritmos se tornaram de uso corrente em muitos outros meios, facilitando um avanço nos cálculos necessários para as mais diversas atividades. Isso era especialmente importante. Na época não havia calculadoras eletrônicas como temos hoje. Pode-se imaginar facilmente em quanto ficou facilitado o trabalho de muita gente, poupando o tempo gasto em longas multiplicações e divisões.
Se você deseja obter mais detalhes, poderá buscar nos vários sites que tratam do assunto.
Curitiba, 28 de junho de 2018
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/adamsdecio
Telefone: (41) 3019-4760
Celulares: (41) 99805-0732

