Estudo da existência dos logaritmos.
Vimos no início do nosso estudo dos logaritmos que
${log_a{b} = x}$, tem como condição de existência que tenhamos:
${a > 0, a ≠ 1}$ ⇔ ${0 < a ≠ 1}$
${b > 0}$
Se estas condições não forem satisfeitas o logaritmo não existe. Isso nos leva a um tipo de expressão em que precisamos analisar uma ou mais situações e estabelecer a condição de existência daquele(s) logaritmo(s) especificamente.
1)Determine a condição de existência do logaritmo da expressão: ${log (x + 2) = 2}$
Observando a expressão temos que:
${ a = 10}$ ⇒ O que satisfaz a primeira condição: ${0<a≠1}$
${b = x + 2}$ ⇒ Como vimos que ${b > 0}$, fica:
${(x + 2) > 0} $ ⇒ Uma inequação do primeiro grau. Vamos resolve-la.
${(x + 2) -2 > 0 -2} ⇔ {(x + 2 – 2) > -2} ⇔ {x > -2}$
${ S = \{x ∈ ℜ| x > -2\}}$
A expressão tem solução, isto é o logaritmo existe, sempre que o valor de $x$ for maior do que ${-2}$.
Podemos determinar o valor de $x$
${log(x + 2) = 2} $
${{10}^2 = x + 2 } ⇔ {100 – 2 = x + 2 – 2} ⇔ {x = 98}$Analise
2)Determine a condição de existência desta expressão.
${log_2{\sqrt{(x-2)}}}$
${ a = 2}$ ⇒A base satisfaz a condição de existência do logaritmo(0< 2 ≠ 1).
${ b = \sqrt{(x-2)}} ⇔ {x – 2 > 0} ⇔ {x – 2 + 2 > 0 + 2} ⇔ {x >2}$
O logaritmo dessa expressão existe para todos os valores de $ {x > 2 }$
${S = \{ x∈ ℜ| x > 2\}}$
3)Analise a existência da expressão logarítmica a seguir.
${log_{1/3}{(-x^2 + 5x – 4)}}$
A base é ${a = 1/3}$ o que a torna diferente de 1 e maior que 0(zero).
O logaritmando é um trinômio quadrado.
${(-x^2 + 5x -4) > 0}$
fazendo: $ {f(x) = – x^2 + 5x -4}$, podemos estudar os sinais da função ${f(x)}$. Para isso vamos igualar o trinômio a 0 (zero) e transformá-lo numa equação do segundo grau.
${ – x^2 + 5x – 4 = 0} ⇔ { a = -1; b = 5; c = -4}$
Vamos calcular o discriminante dessa equação.
${Δ = b^2 – 4\cdot {a}\cdot {c}} ⇔ {Δ =5^2 – 4\cdot{(-1)}\cdot {(-4}}$
${Δ = 25 – 16} ⇔ {Δ = 9}$ ⇒ Discriminante $({Δ > 0})$, significa que a equação possui duas raízes, reais e diferentes.
Determinando as raízes:
${ x = {{-b \pm \sqrt{Δ}}\over {2\cdot {a}}}}$
${x = {{-5\pm\sqrt{9}}\over{2\cdot{-1}}}}$
${x = {{-5 \pm 3}\over{-2}}}$
${x’ = {{-5 + 3}\over{-2}}} ⇔ {x’ = {{-2}\over{-2}}} ⇔ {x’ = 1}$
${x” = {{-5 – 3}\over{-2}}} ⇔ {x” = {{-8}\over {-2}}} ⇔ {x” = 4}$
Para os valores das raízes a função se iguala a 0 (zero), de modo que estes ficam excluídos.
O primeiro termo da função é ${a = -1} ⇔ {a < 0}$. Desse modo o gráfico da função é uma parábola de concavidade voltada para baixo.
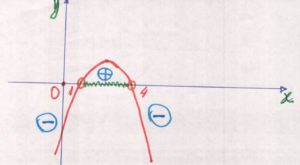
Os valores positivos da função estão localizados acima do eixo das abcissas (x) e portanto a solução para a questão é:
${ S = \{x ∈ ℜ| 1 < x < 4\}}$
4) Estabeleça a condição de existência da expressão logarítmica que segue.
${log_{x -3}{(x + 5)}}$
A base do logaritmo: ${ a = x – 3}$
Vimos que a base deve ser: ${ 0< a ≠ 1}$
Logo: ${x – 3 > 0} ⇔ {x > 3}$
${x – 3 ≠ 1} ⇔ {x ≠ 1 + 3} ⇔ {x ≠ 4} $
O logaritmando deve ser ${ b > 0} ⇔ {x + 5 > 0} ⇔ {x > -5}$
Vamos representar os valores de ${x}$ em duas retas numéricas reais.

Na primeira temos os valores de x que satisfazem a condição necessária para que a base do logaritmo seja possível. Na segunda, os valores maiores que ${-5}$, satisfazem às condições do logaritmando. Fazendo a interseção dos dois conjuntos, temos que:
${S = \{x∈ℜ| 3< x ≠ 4\}}$
5)Faça a análise das condições de existência do logaritmo na expressão a seguir.
${log_{x – 2}{(x^2 – 4x – 5)}}$
Temos que: ${x – 2 > 0} ⇔ {x > 2}$
Também: ${x – 2 ≠ 1} ⇔ {x ≠ 1 + 2} ⇔ {x ≠ 3} $
O logaritmando é também um trinômio quadrado. Vamos transforma-lo em uma função ${f(x)}$.
${f(x) = {(x^2 – 4x – 5) > 0}}$
Determinando as raízes.
${ a = 1, b = -4, c = -5}$
Discriminante: ${ Δ = {b^2 – 4\cdot{a}\cdot{c}}}$
${Δ = {(-4)^2 – 4\cdot{1}\cdot{-5}}} ⇔ {Δ = 16 + 20} $
${Δ = 36}$
Com o discriminante positivo, temos novamente duas raízes reais e diferentes.
${ x = {{-b \pm\sqrt{Δ}}\over{2\cdot{1}}}}$
${ x = {-{(-4)}\pm\sqrt{36}\over{2}}}$
${x = {{4\pm6}\over2}}$
${x’ = {{4 + 6}\over2}} ⇔ { x’ = 10/2} ⇔ {x’ = 5}$
${x” = {{4 – 6}\over 2}} ⇔ {x” = -2/2} ⇔ {x” = – 1}$
O primeiro termo da função é positivo, portanto a parábola terá concavidade para cima. Os valores da função são positivos para valores externos ao intervalo das raízes. Mas para os valores de x menores que -1, a base do logaritmo não existe e portanto ficamos somente com os maiores que 5. Veja no gráfico.
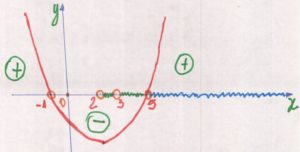
Isso nos permite dizer que:
${S=\{x∈ℜ|x > 5\}}$
Exercícios para treinar. Baseado nos exemplos anteriores, faça a análise das condições de existência dos logaritmos.
a) ${log{(x^2 – 7x + 12)}}$
b) ${log(3x – 6)}$
c) ${log_{(5)^{-1}}{\sqrt{x – 25}}}$
d)${log_{x – 2}{(-x^2 + 7x – 10)}}$
e)${log_{x + 5}{x – 7}}$
f)${log_{1/3}{(x^2 – 3x – 10)}}$
g)${log_{5-x}{(x^2 – 6x + 8)}}$
h)${log_{\sqrt{x + 3}}{\sqrt[3]{(x + 5)^2}}}$
Tenha um bom desempenho e não esqueça. Em caso de dúvida, peça ajuda por um dos canais abaixo listados.
Curitiba, 09 de julho de 2018
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/adamsdecio
Telefone: (41) 3019-4760
Celulares: (41) 99805-0732

